摘要:
在生物系统和生命活动中,酶都发挥着非常重要的作用,并且参与了几乎所有的化学反应。因此,酶动力学的分析对化学反应的研究至关重要。所以从二十世纪早期就有许多专家学者致力于对酶促系统进行动力学分析,并且做出了许多杰出的贡献。酶动力学的分析对于研究如何控制酶的活性,如何利用药物控制酶,以及酶在代谢中的作用等均有重要作用。本文通过严格的数学分析基础的酶动力学模型,即包含单一底物被酶催化转化为单一产物的反应模型,基于计算机代数技术和动力系统的定性理论。本文的方法是在没有任何假设的情况下提出的并且得到了模型的解析解。在文章的最后给出了一些例子来验证该方法并给出曲线表示。此外,该方法也可以用于研究其它学科,例如生物物理等。
Abstract:
Enzyme plays an important role in the living system as well as life process, and is involved in almost every chemical reaction; thus the enzyme kinetics is fundamental to the research of the chemical reactions. Therefore, from the early part of twentieth century, many researchers were dedicated to the study of the analysis of kinetics of enzymatic system, and a lot of excellent work has been done, because the analysis of the enzyme kinetics can help us find how the activity of enzyme is controlled, how the drug inhibits the enzyme, its role in metabolism, and so on. In this paper, we present a method by rigorous mathematics to analyze the general enzyme kinetics model, which is concerned with a single substrate catalyzed by enzyme and transformed into a single product, and it is based on computer algebra technique and the qualitative theory of dynamical system. Our method does not need any assumption and all the solutions here are analytical. Finally, some examples are given to test this method and make it readable by simulated progress curves, so that almost everyone may understand it. Furthermore, the techniques in this study can be used to the research of other disciplines, such as biophysics, and so on.
1. 引言
酶促系统的动力学研究是指研究由酶来催化的化学反应的动力学模型。研究酶动力学可以帮助我们研究酶的催化机理,酶对生命活动过程的影响和如何控制酶促反应等[1] 。因此,酶促系统的分析对研究生命系统起到非常重要的作用。
Adrian Brown在1902年首次开始研究酶动力学并提出了最基础的酶动力学模型,其中包含单一底物被酶催化生成单一产物 [2] 。之后,包含单一底物的酶促反应已经被国内外学者深入地进行了研究。著名的米氏方程由Briggs和Haldane提出 [3] ,该方程在分子等级的化学反应中是适用的。Lineweaver和Burk提出了用来确定米氏方程的参数值的方法 [4] 。Victor Henri提出了包含单一底物,单一产物和酶–底物复合物的两个反应机理 [5] [6] ,还有一些非常重要的最简单的酶动力学模型的分析可以在文章 [7] 中找到。
在分析最简单的酶促系统的动力学的过程中通常会遇到一些非常复杂的代数表达式,这些表达式使得动力学分析变得十分困难,因此需要一些工具来对酶反应的动力方程进行分析。计算机代数理论可以处理大量的数学表达式和进行复杂的符号计算 [8] - [12] ,该理论对没动力学的研究也起到非常重要的作用。
动力系统的定性理论研究有着悠久的历史 [13] ,该理论已被应用到生物理论的研究中,包括酶动力学的研究 [14] - [16] 。本文运用该理论和计算机代数系统来分析最简单的酶促系统的动力学数据。本文所提出的方法的最大特点即没有在任何假设的情况下对酶促系统进行动力学分析,且该方法中的运算可以在Maple中进行并得到解析解。此外,本文所提出的方法通过了严谨的数学推导。
本文所提出的理论将在第二部分给出,文章的第三部分会给出一些例子来标明该方法的实用性和有效性。
2. 方法
酶促系统的研究通常会在一些假设下进行,但是本文将提出一种在不包含任何假设下对含有三个速率常量的化学反应的动力学分析。
最简单的酶动力学模型包括两个步骤。第一步是底物 被酶
被酶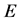 催化,转化为混合物
催化,转化为混合物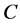 ,转化速率为
,转化速率为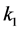 ,逆反应速率为
,逆反应速率为 ;第二步时混合物分解为产物
;第二步时混合物分解为产物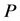 和酶
和酶 ,速率为
,速率为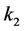 。模型可以表示为如下形式
。模型可以表示为如下形式
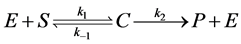 . (1)
. (1)
设 ,
,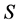 ,
,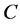 和
和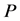 分别表示酶,底物,复合物和产物在反应过程中的浓度。则该模型可以被描述为如下的常微分方程组 [17] :
分别表示酶,底物,复合物和产物在反应过程中的浓度。则该模型可以被描述为如下的常微分方程组 [17] :
 (2)
(2)
方程组的初始条件为
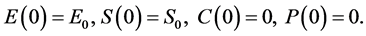 (3)
(3)
结合上初始条件,该模型为一个初值问题。由于该系统为非线性的,无法得到解析解。考虑化学方程式中存在如下的守恒关系
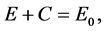 (4)
(4)
 (5)
(5)
通过上述等式,可得
 (6)
(6)
则系统(2)等价于如下系统
 (7)
(7)
其中
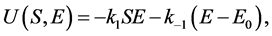 (8)
(8)
 (9)
(9)
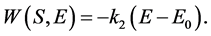 (10)
(10)
下面的定理对本文方法非常重要。
定理2.1. 考虑如下常微分方程组系统
 (11)
(11)
其中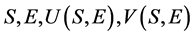 为(8),(9)所示。则可以得到
为(8),(9)所示。则可以得到
1) 系统(11)有唯一的稳定结点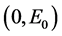 ;
;
2) 系统(11)在点 的线性部分为
的线性部分为
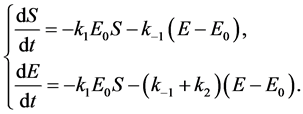 (12)
(12)
证明. 1) 利用计算机代数理论解下述常微分方程组系统
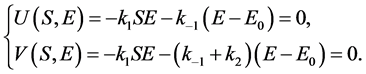 (13)
(13)
得到唯一解 ,因此该解为系统(11)的唯一平衡点 [18] 。
,因此该解为系统(11)的唯一平衡点 [18] 。
2) 通过对 和
和 在点
在点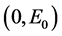 进行一阶泰勒展开 [19] ,可以得到系统(11)的线性部分如下所示
进行一阶泰勒展开 [19] ,可以得到系统(11)的线性部分如下所示
 (14)
(14)
此外可以得到该系统的系数矩阵为
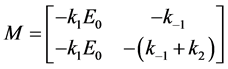
该矩阵的特征多项式为
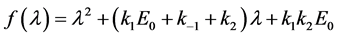
利用Maple解等式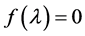 ,由于方程中的
,由于方程中的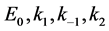 均不为负数,则可得到矩阵
均不为负数,则可得到矩阵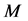 的两个负的特征根
的两个负的特征根

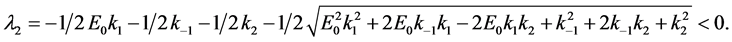
根据动力系统理论,点 是一个稳定的结点。
是一个稳定的结点。
通过定理2.1可以将系统(7)转化为如下的线性系统
 (15)
(15)
其系数矩阵形式可表示为
 (16)
(16)
使用Maple中的dsolve命令可在2秒钟之内得到系统(16)的解析解集。代入等式(3)中给出的初值并用subs命令重新整理结果,可得到系统的解析解如下所示
 (17)
(17)
 (18)
(18)
 (19)
(19)
其中
 (20)
(20)
在本文中,所有的计算均在Maple中进行,该软件可以高效得进行符号计算。所用程序在一台Core(TM) i5-4260U,4096 MB内存的苹果笔记本电脑中运行。
3. 总结
本文在分析最简单的酶促系统的动力学模型时遇到了非常复杂的代数表达式,计算这些表达式需要大量的时间和空间。计算机代数是一个非常强大的理论,可以快速的解决这些问题。在本文运用计算机代数理论和动力系统理论来得出常微分方程组系统的解析解,该解析解即为最简单的酶促系统的动力学模型的解。在稳定平衡点上,该系统被化为线性系统,利用Maple软件计算得出的结果与文章 [11] 在假设 时所得出的结果完全一致。
时所得出的结果完全一致。
在图1中,给定一组速率常量与底物和酶的初始浓度,画出 ,
,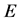 ,
,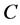 和
和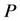 的浓度曲线。由于各个浓度之间差距较大,本文用3张图片来展示所有曲线。所使用的速率常数为:
的浓度曲线。由于各个浓度之间差距较大,本文用3张图片来展示所有曲线。所使用的速率常数为: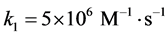 ,
,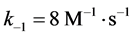 和
和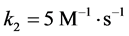 ,给定的初始浓度为
,给定的初始浓度为 ,
,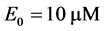 。图1(a)中为
。图1(a)中为 和
和 的浓度曲线,图1(b)中为
的浓度曲线,图1(b)中为 ,图1(c)中为
,图1(c)中为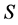 。
。
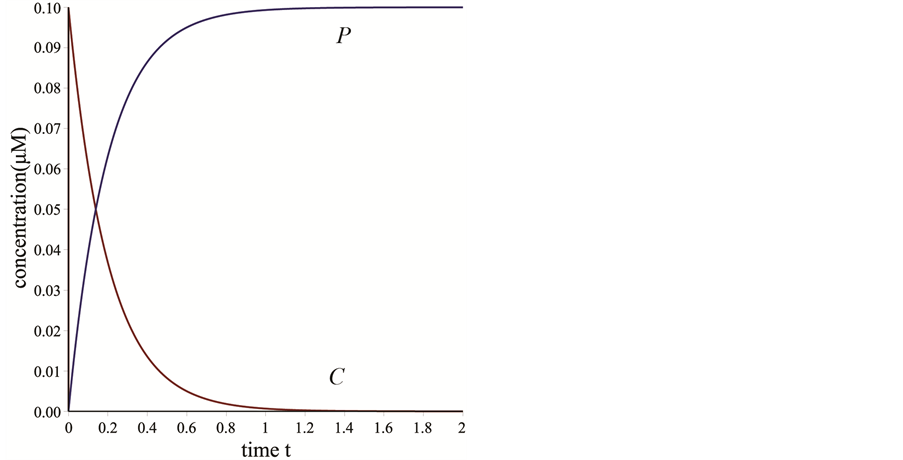
从图1(a)中可以看出, 的浓度随着时间的增加而增加,在后期,随着底物
的浓度随着时间的增加而增加,在后期,随着底物 耗尽,曲线趋于平稳。
耗尽,曲线趋于平稳。 在2秒左右时减少到零。在图1(b)中,
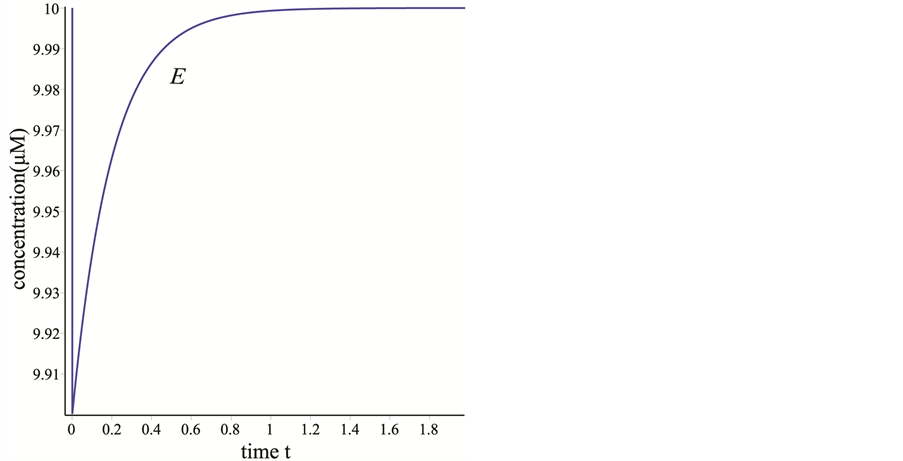
在2秒左右时减少到零。在图1(b)中, 的浓度为另一种情况。
的浓度为另一种情况。 的浓度迅速的减少到9.90,然后缓慢的增加直到平稳。在图1(c)中,在反应开始时,
的浓度迅速的减少到9.90,然后缓慢的增加直到平稳。在图1(c)中,在反应开始时, 的浓度快速的减少,然后缓慢的降低,在2秒左右时降低到零。
的浓度快速的减少,然后缓慢的降低,在2秒左右时降低到零。
 (a) (b)
(a) (b)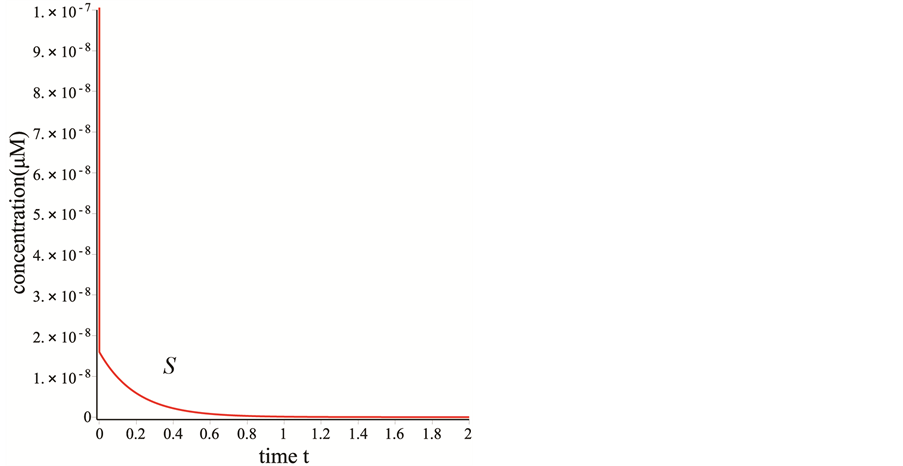 (c)
(c)
Figure 1. (a) The simulated curves of P and C; (b) The simulated curves of E; (c) The simulated curves of S
图1. (a) P和C的模拟曲线;(b) E的模拟曲线;(c) S的模拟曲线
致谢
本文由国家自然科学基金(11101029)和中央高校基本科研基金(610806)提供支持。