1. 引言
流体力学研究在各种力的作用下流体本身的状态,以及流体和固体壁面、流体和流体间、流体与其他运动形态之间的相互作用的力学分支。不同流体之间流动时,总有界面的存在。因此界面问题一直是流体力学中常见备受关注的问题。提到界面问题计算方法的历史,我们首先追溯到20世纪70年代,Peskin 和McQueen使用浸入边界法模拟心脏瓣膜在心脏收缩和舒张过程中的开启与闭合,分析心脏内部血液的流动情况。他们成功模拟了心脏的周期运动,通过数值模拟分析在不同时刻心脏内外的速度场和压强场的变化情况,并对比了心脏内部为天然瓣膜和几种不同的人造瓣膜条件下心脏中的血液流动情况,这里心脏瓣膜可以视为一种不可渗透的材料界面,各个心脏房与心脏室之间的血液并不会通过界面渗透,而人体中的细胞膜是一种半渗透膜,细胞内外的物质会通过细胞膜选择性地渗透。此类弹性膜结构的内部与外部均为流体介质。这种膜结构相当于流场中的一个内边界。随后的相关方法研究者们致力于提高界面问题求解方法的精度。如1992年Beyer和Leveque分析了与时间无关的界面问题,通过选择合适的离散,可以将数值精度提高到二阶。1994年LeVeque和Zhilin Li [1] 在SIAM上发表了篇关于浸入界面方法的论文,引起个很多学者的重视,从而掀起了界面问题数值方法研究的大幕。
对界面问题的数值方法,分为两类不同的策略:1) 自适应方法;2) 一致网格方法,在界面附近修改计算格式。
2. 界面问题及浸入界面方法简介
2.1. 界面问题
本模板流体力学中的界面问题分为以下几类:1) 流–流型自由表面问题;2) 流固耦合问题;3) 材料的界面问题 [2] 。我们知道流体力学中几种经典的数值方法,在此我们主要以有限差分法来做简单介绍:有限差分法(Finite Difference Method) [3] ,构造简单,成熟,也可构造高精度格式。是很多工程软件工程计算中常用的研究者最常用而且成熟的方法。有限差分法的基本思想是把连续的定解区域用有限个离散点构成的网格来代替,这些离散点称作网格的节点,把连续定解区域上的连续变量的函数用在网格上定的离散变量函数来近似;把原方程和定解的微商用差商来近似积分用积分和来近似。于是原微分方程和问题在离散点上的近似解。然后再利用插值方法便可以通过离散解得到定解问题在整个区域上的近似解。构造差分的方法有多种形式,目前主要采用的是泰勒级数展开方法。本文中研究的浸入界面方法也是采用泰勒级数展开方法得到的差分格式。这种方法比较适合相对简单外形的高精度计算,它的缺点就是处理复杂边界不够灵活。虽然界面问题计算发展已经做了很多的工作,基于上述专家的工作,本文对部分内容做了改进和创新。本文侧重计算方法的改进,因此在求解模型中主要是以简单的椭圆问题为例展开阐述的。本文的工作主要通过以下几个方面展开的。
对于椭圆界面问题,通过分析和模拟浸入界面方法,我们改进了方法的构造形式,我们从最简单的一维问题入手,如果在某个节点处函数有不连续的情况,直接采用中心差分连续的计算显然是不对的,我们采取的办法是远离间断点处节点使用标准的中心差分,这一点和其他的浸入界面方法思路相同,在含有间断点的单元上,直接采取当以该点为界的分段二次函数来近似该单元的函数,相邻节点(单元节点及间断点)都用泰勒公式在中心节点展开得到的函数关系,根据它的函数值的间断和导数的间断,以及根据方程本身的信息,可以得到三个关系式,然后采用待定系数方法,求出不规则节点处的差分格式,最后全部节点的差分格式联立求出离散节点的函数值 [1] 。
对于热传导界面问题,我们同样采取椭圆方程中改进浸入界面的思想,采用在点处展开的Taylor展开式。时间方向采取Crank-Niclson格式,加上初值条件的离散,可以构造求解一维的带界面的热传导方程的浸入界面格式方法。
2.2. 浸入界面方法介绍
本模板首先,回顾一下应用一维问题浸入界面方法 [1] [4] [5] 求方程

其中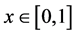 ,在
,在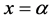 时是不连续的。
时是不连续的。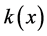 ,
, 为连续函数。在
为连续函数。在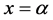 处强加两个不连续的连接条件
处强加两个不连续的连接条件
 (1)
(1)
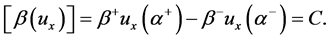 (2)
(2)
 (3)
(3)
根据问题我们希望构造如下形式的差分格式 [6]
 (4)
(4)
进而,得到如下的三对角矩阵。
 (5)
(5)
当单元中不含 点时,格式为标准的中心差分格式,即上式中各系数取为
点时,格式为标准的中心差分格式,即上式中各系数取为
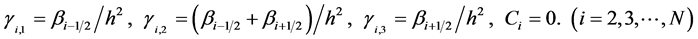
这里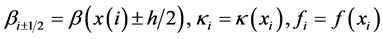 此时截断误差为
此时截断误差为 。当单元中含有间断点
。当单元中含有间断点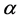 时,即
时,即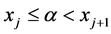 。有两个特殊单元
。有两个特殊单元 和
和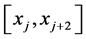 处需要特殊计算。
处需要特殊计算。
3. 改进的浸入界面方法求解一维椭圆问题
3.1. 含一个间断节点情形的差分格式构造
首先在一个特殊单元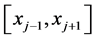 考虑,我们将
考虑,我们将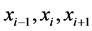 节点处的 u 值在
节点处的 u 值在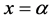 处泰勒展开。以第一个特殊单元
处泰勒展开。以第一个特殊单元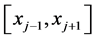 为例,当
为例,当 时,我们将
时,我们将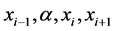 节点处的u值在
节点处的u值在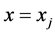 处泰勒展开。最后采用插值法,对其进行适当的泰勒展开。
处泰勒展开。最后采用插值法,对其进行适当的泰勒展开。
根据两个连接条件(2) (3)以及方程组(6),我们可以得的关系
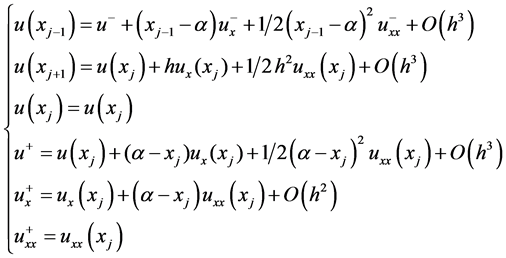 (6)
(6)
除此之外又因为
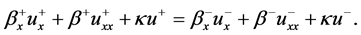
利用截断误差表达式,待定系数方法确定。
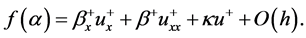
设各系数 和
和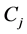 关系如下:
关系如下:
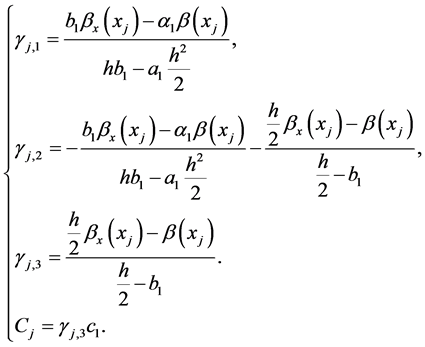 (7)
(7)
设各系数 关系如下:
关系如下:
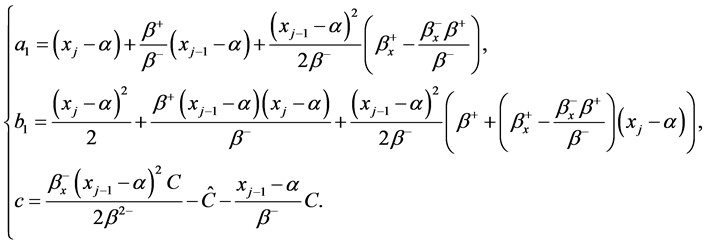 (8)
(8)
我们考虑另一个特殊单元 ,当
,当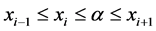 时,
时, 处
处 的值在
的值在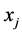 处进行泰勒展开。
处进行泰勒展开。
 (9)
(9)
根据两个连接条件(2) (3)以及方程组(9),我们可以得 的关系根据上式得到
的关系根据上式得到


利用截断误差表达式,待定系数方法确定。
待定系数方法确定 和
和 。
。
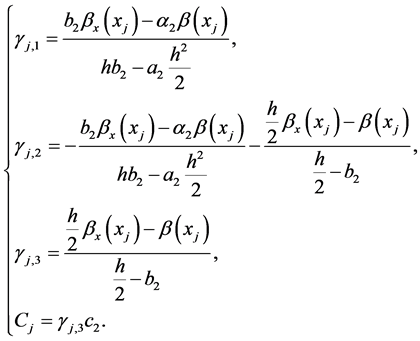 (10)
(10)
各系数 关系如下:
关系如下:
 (11)
(11)
3.2. 含两个间断节点情形的差分格式构造
下面我们考虑在所讨论单元中含有两个节点的情况。此处回顾一下该浸入界面方程

直接采取当以该点为不连续点的分段二次函数来近似该单元的函数,相邻节点(单元节点及间断点)都用泰勒公式在中心节点展开得到的函数关系,根据它的函数值的间断和导数的间断,以及根据方程本身的信息,可以得到三个关系式,然后采用待定系数方法,求出不规则节点处的差分格式。来拟合出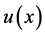 的方程,同样的,我们还是采用插值法,对其进行泰勒模拟。由于在处不连续。并且记
的方程,同样的,我们还是采用插值法,对其进行泰勒模拟。由于在处不连续。并且记
 (12)
(12)
 (13)
(13)
首先我们考虑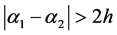 时,我们知道其差分格式可按照上述一个节点的情况,分别考虑。下面我们考虑当时
时,我们知道其差分格式可按照上述一个节点的情况,分别考虑。下面我们考虑当时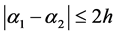 ,我们知道此时有三种情况,分别是:
,我们知道此时有三种情况,分别是:
1) 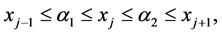
2) 
3) 
1) 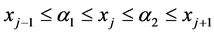
通过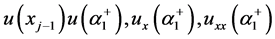 和
和 在
在 点处的泰勒展式,再结合上述一个节点的情况,进而得到
点处的泰勒展式,再结合上述一个节点的情况,进而得到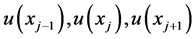 的关系,用以下形式表出
的关系,用以下形式表出
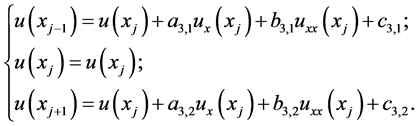 (14)
(14)
通过使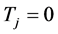 ,我们可以确定三对角矩阵各项系数,从而进行拟合运算。
,我们可以确定三对角矩阵各项系数,从而进行拟合运算。
 (15)
(15)
然后代入三对角矩阵(5),通过Matlab求解,即可得到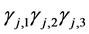 的值。其中
的值。其中
 (16)
(16)
 (17)
(17)
2) 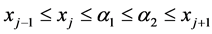
对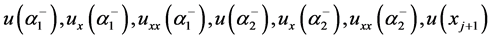 ,在
,在 点处的泰勒展式,再结合上述一个节点的情况,和连接条件(4) 进而得到
点处的泰勒展式,再结合上述一个节点的情况,和连接条件(4) 进而得到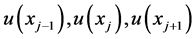 的关系,用以下形式表出
的关系,用以下形式表出
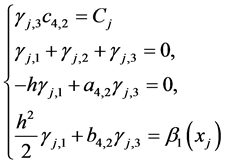 (18)
(18)
然后代入三对角矩阵(5),通过Matlab求解,即可得到 的值。其中
的值。其中
 (19)
(19)
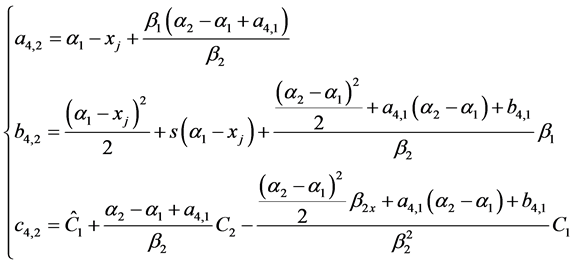 (20)
(20)
3) 
在 点处的泰勒展式,再结合上述一个节点的情况,和连接条件(4)进而得到的关系。进而得到
点处的泰勒展式,再结合上述一个节点的情况,和连接条件(4)进而得到的关系。进而得到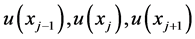 的关系。
的关系。
使 ,我们可以确定三对角矩阵各项系数,从而进行拟合运算。其中
,我们可以确定三对角矩阵各项系数,从而进行拟合运算。其中
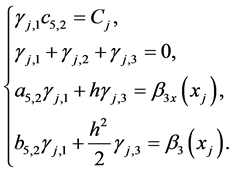 (21)
(21)
然后代入三对角矩阵(5),通过Matlab求解,即可得到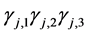 的值。其中
的值。其中
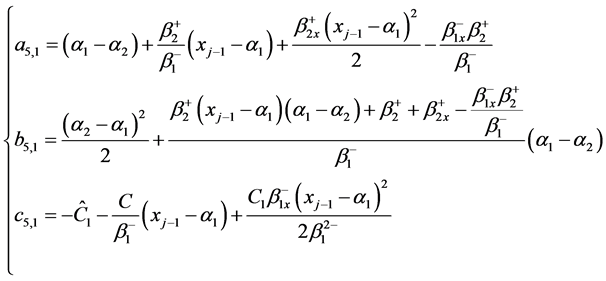 (22)
(22)
 (23)
(23)
4. 改进的浸入界面方法求解一维热传导问题
前面我们介绍的是基于不含时间项的椭圆浸入界面问题,后面我们将此改进方法运用在简单的热传导问题模型中,我们考虑的模型为考虑区域为 中间由一条内部界面
中间由一条内部界面 分隔,内部界面在
分隔,内部界面在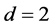 时通常是条曲线。
时通常是条曲线。
 (24)
(24)
初始条件
 (25)
(25)
Dirichlet边界条件
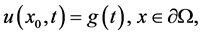 (26)
(26)
这里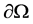 是外部边界,扩散系数
是外部边界,扩散系数 和源项
和源项 在每个子区域是连续,但是在通过界面
在每个子区域是连续,但是在通过界面 时出现跳跃,即
时出现跳跃,即
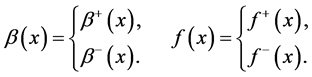 (27)
(27)
如果没有界面的连续问题我们知道,在上述椭圆界面中已经实现,下面,我们将采用改进Crank- Nickson格式的浸入界面方法来叙述。
改进的浸入界面方法求解一维热传导定界面问题
 ,连续的扩散方程的Crank-Nickson格式为
,连续的扩散方程的Crank-Nickson格式为
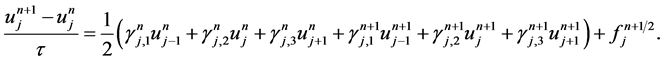 (28)
(28)
其中

对于连续问题,本格式是截断误差为 的无条件稳定的数值算法。
的无条件稳定的数值算法。
假设源函数中有奇异项

可以得到在 处的不连续条件
处的不连续条件
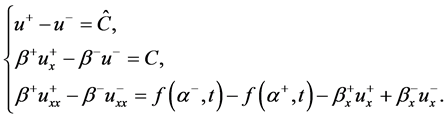 (29)
(29)
我们可以看出连接条件与时间 相关。我们同样采取椭圆方程中改进浸入界面的思想,Taylor展开式我们采用在
相关。我们同样采取椭圆方程中改进浸入界面的思想,Taylor展开式我们采用在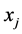 展开。具体差分情况详见[3.1]含一个间断节点情形的差分格式构造时的情况。整理可得到
展开。具体差分情况详见[3.1]含一个间断节点情形的差分格式构造时的情况。整理可得到
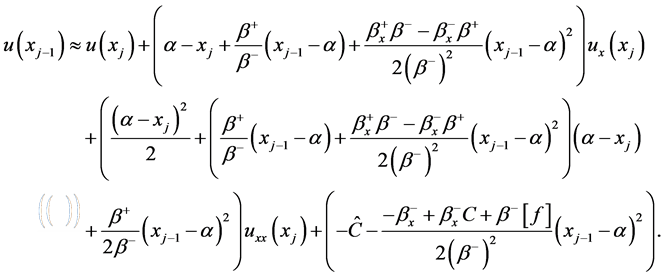 (30)
(30)
根据

利用待定系数方法得到三元一次方程组,求出系数 。
。
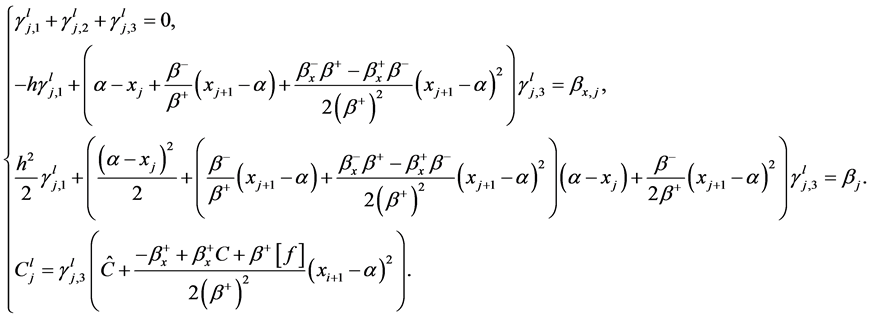 (31)
(31)
时间离散仍然考虑Crank-Nickson格式,在这两种特殊单元下,将求解的系数 及连接常数
及连接常数 。
。
 (32)
(32)
移项将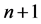 层函数左移,得
层函数左移,得
 (33)
(33)
加上初值条件,一维的带界面的热传导方程的浸入界面格式就确定了。从局部截断误差上看,仅有两个单元的截断误差O(h),规则单元的均为,时间导数项为二阶的,因此整体的误差阶为。
5. 数值算例
5.1. 算例1
我们下面先考虑只有一个间断点的精确解算例,假设讨论区间都在[a, b],即取a = 0,b = 1。
真解如下式
 (34)
(34)
取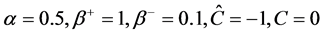 ,步长
,步长 ,利用改进的浸入界面方法求解。数值结果见表1和图1,表明当函数
,利用改进的浸入界面方法求解。数值结果见表1和图1,表明当函数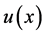 为分段二次函数时,采用浸入界面方法可以精确的得到该问题的解,误差为机器误差。该算例的截断误差如表1。这里
为分段二次函数时,采用浸入界面方法可以精确的得到该问题的解,误差为机器误差。该算例的截断误差如表1。这里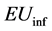 是无穷范数误差,
是无穷范数误差, 是L2范数误差,当改进的浸入界面方法求解此问题时,得到的误差为机器误差,因此随着剖分加密,机器误差的累积使得剖分越密,误差越大。
是L2范数误差,当改进的浸入界面方法求解此问题时,得到的误差为机器误差,因此随着剖分加密,机器误差的累积使得剖分越密,误差越大。

Table 1. Two types of errors for example 1
表1. 算例1两种误差

Figure 1. The error distribution for example 1 
图1. 算例1误差图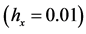
5.2. 算例2
我们考虑在单元内存在两个节点的情况
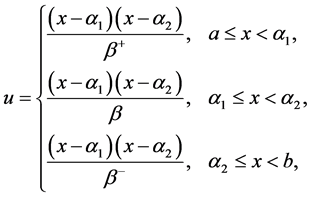 (35)
(35)
取
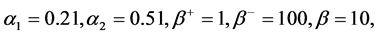 步长h = 0.1,0.01,0.001,利用改进的浸入界面方法求解。同上算例1,表明当函数为分段二次函数时,采用浸入界面方法可以精确的得到该问题的解,误差为机器误差该算例的截断误差如表2,误差分布结果参看图2。
步长h = 0.1,0.01,0.001,利用改进的浸入界面方法求解。同上算例1,表明当函数为分段二次函数时,采用浸入界面方法可以精确的得到该问题的解,误差为机器误差该算例的截断误差如表2,误差分布结果参看图2。
5.3. 算例3
下面再取一个形如一般一元分段高次函数,假设讨论区间都在[0, 1],即取a = 0,b = 1,真解如下式

取步长,利用改进的浸入界面方法求解。数值结果见表4,表明当函数为分段二次函数时,采用浸入界面方法可以精确的得到该问题的解,误差为机器误差。该算例的截断误差见表3。
该算例截断误差图参看图3。

Table 2. Two types of error for example 2
表2. 算例2不同步长的两种误差

Table 3. The errors and orders for example 3
表3. 算例3不同步长的误差及误差阶
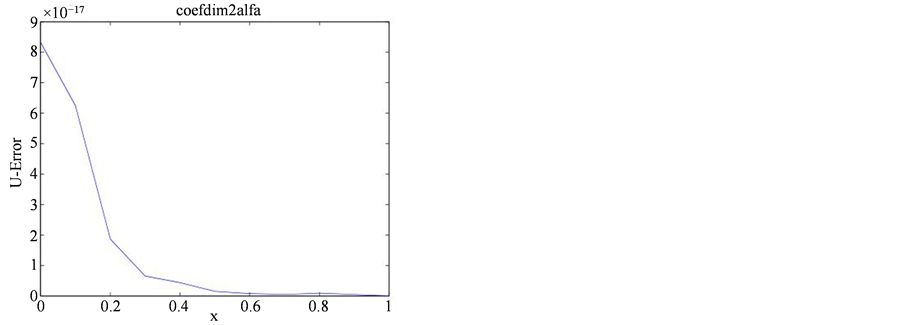
Figure 2. The error distribution for example 2 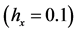
图2. 算例2误差图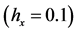
5.4. 算例4
算例4 一维固定界面的热传导问题,假设在界面处解是连续的,通量也是连续的真解问题

初边值条件由真解给出

表4给出了改进的浸入界面方法的求解算例4的数值结果。分别给出了时间τ = 0.001,h = 0.1,h = 0.05,0.025,0.0125的误差及误差阶,图4给出算例4在t变化时的误差变化情况。

Table 4. The errors and orders for example 4
表4. 算例4不同步长的误差及阶
6. 结论及创新点
1) 首先求解此类问题时,我们了解到李志林教授所提出的方法即在点处进行展开差分,但考虑到拟合精度的优良性,我们对其差分格式进行了修改。即我们主要是在点处进行泰勒展开。将其精度调至三阶。并对其进行了算例检验。2) 基于上面我们所推导方法,对其运用在了热传导问题中。
致谢
感谢审稿人为本论文提出的宝贵意见。
基金项目
新疆维吾尔自治区自然科学基金资助项目(No. 2015211C289)。