1. 引言
启发式教学[1] 是一种民主、科学的教学思想和教学原则。它要求教师在整个教学过程中,以各种方式启发学生积极思考,激发学生潜在的学习动机,使其主动、热情地参与学习活动。在数学学习中,采用灌输式教学,学生容易感到枯燥无味。被动填圧式的课堂教学,单调严谨的逻辑推理,学生容易失去对数学的学习兴趣。生动活泼的启发式教学则能顺应学生好奇的特点,调动学生学习的积极性和主动性,引导学生在数学乐园中自由探索的兴趣。
微分中值定理[2] -[10] 是罗尔定理、拉格朗日中值定理、柯西中值定理和泰勒中值定理的统称。其中拉格朗日中值定理是微分中值定理的核心,建立了函数值与导数值之间的定量关系。罗尔定理是拉格朗日中值定理的特殊情况,柯西中值定理是拉格朗日中值定理的推广。微分中值定理是微分学的核心内容和理论基础。 它是应用导数的局部性质研究函数全局性质的重要工具;它使得导数理论用于函数形态的研究成为可能,显示了导数理论、微分学强大功能和广泛的应用性。 因此,学好微分中值定理能为进一步学好微积分理论打下坚实的理论基础[2] [3] 。微分中值定理是微分学教学的重点和难点[2] -[5] 。一方面,微分中值定理产生的根源比较隐蔽,没有明显的物理和几何背景,造成学生在认知过程上的困难。另一方面,微分中值定理解决的是存在性问题,其本身具有高度的抽象性,造成学生在理解上的困难。
为了帮助学生理解掌握微分中值定理,本文在总结教学经验的基础上,优化教学设计,对微分中值定理的教学模式进行探讨。采用观察分析、引导发现和直观演示相结合的教学手段, 采用启发式教学方法,推行师生互动,使用口头和文字提问,循循善诱,步步深入,灵活运用探索性学习方式,培养学生自主学习的意识,让学生在自主探索中学会学习,建立自己的知识体系。在教学中,启发、诱导贯穿始终,激发学生的学习兴趣,调动学生学习的积极性,充分发挥学生在教学中主体能动作用。
2. 引导学生发现微分中值定理的具体内容
2.1. 启发学生归纳总结拉格朗日中值定理
实物观察启发:通过具体直观的演示,由直觉上升到理性认识。
设 ,
, 表示一条有始有终的连续光滑曲线AB,如图1。
表示一条有始有终的连续光滑曲线AB,如图1。
质疑启发:图1中曲线AB上是否存在一点M,满足曲线在M点的切线平行弦AB?
自主探索:学生自己找到M点,画出切线MN,如图2。
引导学生猜测:一条有始有终的连续光滑曲线AB上至少存在一点M,满足曲线在M点的切线平行弦AB。
教师启发性提问:这个结论是否具有普遍性,背后是否隐藏着一般的数学原理?

Figure 1. A continuous and smooth curve AB
图1. 一条连续光滑的曲线AB

Figure 2. Tangent MN which is paralled with chord AB
图2. 平行于弦AB的切线MN
引导学生得出一般性结论:
1) 一条有始有终的连续光滑曲线AB用数学语言描述就是函数 满足
满足
① 在区间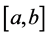 上连续;② 在区间
上连续;② 在区间 内可导。
内可导。
2) 曲线AB上至少有一点 ,使得过M点的切线MN与弦AB平行,即两者的斜率相等。由导数的几何意义可知切线MN的斜率是
,使得过M点的切线MN与弦AB平行,即两者的斜率相等。由导数的几何意义可知切线MN的斜率是 ,而弦AB的斜率是
,而弦AB的斜率是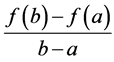 。因此,至少存在一点
。因此,至少存在一点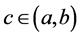 ,使得
,使得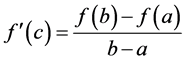 。
。
总结概括、加深理解:
拉格朗日中值定理:
若函数 满足:① 在区间
满足:① 在区间 上连续;② 在区间
上连续;② 在区间 内可导,则至少存在一点
内可导,则至少存在一点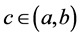 ,使得
,使得

2.2. 启发学生对定理探索研究,引导学生自己得到柯西中值定理和罗尔定理
教师引导:若拉格朗日中值定理中的连续函数的端点的函数值相等,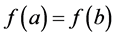 ,定理发生什么变化?
,定理发生什么变化?
学生发现:在这种情况下,图2变成了图3,且定理变成了:
若函数 满足:① 在区间
满足:① 在区间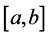 上连续;② 在区间
上连续;② 在区间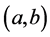 内可导;③
内可导;③
 ,则至少存在一点
,则至少存在一点 ,使得
,使得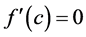 。(这就是罗尔定理)
。(这就是罗尔定理)
教师引导:如果曲线AB不用 表示,而用参数方程
表示,而用参数方程
 表示那么拉格朗日定理又会发生什么变化?(见图4)。
表示那么拉格朗日定理又会发生什么变化?(见图4)。
引导学生:由参数方程求导法可知,如果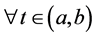 ,
, ,
,
那么切线MN的斜率 ,
,
而弦AB的斜率 。
。
总结概括得到柯西中值定理:
若函数 ,
, 满足:① 在区间
满足:① 在区间 上连续;② 在区间
上连续;② 在区间 内可导;③
内可导;③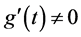
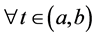 ,则至少存在一点
,则至少存在一点 ,使得
,使得

因此,柯西中值定理可以看成是含有参数形式的拉格朗日中值定理。
2.3. 引导学生理解微分中值定理的内涵和外延
教师提问:比较柯西中值定理、拉格朗日中值定理和罗尔定理之间的关系?
自主探索:在上面的探求中,容易发现罗尔定理是拉格朗日中值定理的特殊情形。进一步地,引导学生发现在柯西中值定理中,特别地,取 ,
, ,那么就得到拉格朗日中值定理。因此,拉格朗日中值定理是柯西中值定理的特殊情形。
,那么就得到拉格朗日中值定理。因此,拉格朗日中值定理是柯西中值定理的特殊情形。

质疑启发:下面对柯西中值定理的证明是否正确?
因为函数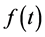 ,
, 在区间
在区间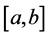 上都满足拉格朗日中值定理的条件,所以至少存在一点
上都满足拉格朗日中值定理的条件,所以至少存在一点 ,满足
,满足 ,
, 。又由于
。又由于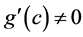 ,因此,
,因此,

Figure 3. A continuous and smooth curve AB which has the same height at endpoints
图3. 两端点等高的连续光滑的曲线AB
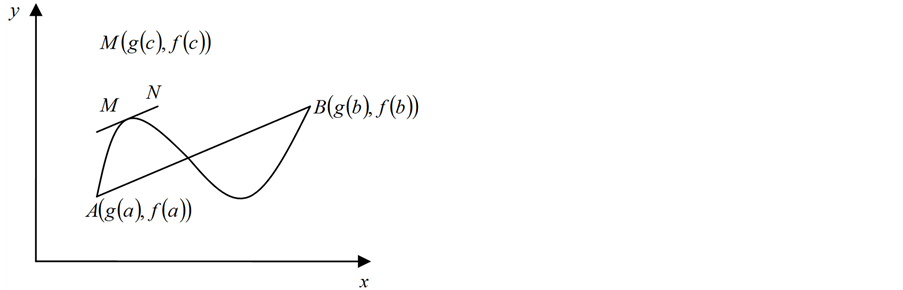
Figure 4. A continuous and smooth curve AB which is represented by parametric equation
图4. 用参数方程表示的连续光滑曲线AB
学生自主探索:证明过程错误,因为对于不同的函数 ,
, ,存在的
,存在的 点(即中值)不一定相同。
点(即中值)不一定相同。
3. 深入剖析微分中值定理
3.1. 验证定理
引导学生思考怎样用特殊证明一般。在定理证明中,以罗尔定理为基础,构造辅助函数,使其满足罗尔定理的条件。通过构造辅助函数证明微分中值定理是一种常用且有效的方法[5] [6] 。如何构造辅助函数是定理证明的重点和难点。一般地,构造的辅助函数并不唯一。
按教科书[9] 讲授罗尔定理的证明。(略)
3.1.1. 拉格朗日中值定理的证明
教师提问:大家能否构造一个辅助函数,借助该辅助函数,利用罗尔定理证明拉格朗日中值定理?引导学生构造辅助函数:
1) 解析法
根据定理的条件和结论,从结论出发,采用倒推分析的方法,构造辅助函数 。拉格朗日中值定理的证明思路分析图,如图5。
。拉格朗日中值定理的证明思路分析图,如图5。
用解析法构造辅助函数是应用微分中值定理解题常用且有效的一种方法。
2) 图像法
教师引导:拉格朗日中值定理与罗尔定理的不同之处?
学生自主探索:发现拉格朗日中值定理比罗尔定理少了一个条件: 。
。
引导学生:构造一个辅助函数 满足罗尔定理的条件,特别地,
满足罗尔定理的条件,特别地, 。
。
观察几何图形发现:弦AB与曲线AB在两端点的函数值相等。因此,曲线AB在两端点的纵坐标与弦AB在对应点的纵坐标之差相等。由此构造辅助函数 。验证
。验证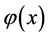 满足罗尔定理的条件,进而证明拉格朗日中值定理。
满足罗尔定理的条件,进而证明拉格朗日中值定理。
3.1.2. 柯西中值定理的证明
教师提问:类似以上拉格朗日中值定理的证明,请构造辅助函数证明柯西中值定理。
引导学生:比较拉格朗日中值定理和柯西中值定理的结论?
学生自主探索:比较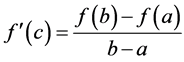 和
和 发现,把拉格朗日中值定理中的
发现,把拉格朗日中值定理中的 ,
, ,
, 分别换成
分别换成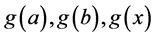 就是柯西中值定理的结论。
就是柯西中值定理的结论。
引导学生大胆猜测:把证明拉格朗日中值定理的辅助函数 中的
中的 ,
, ,
, 分别换成
分别换成 能否得到证明柯西中值定理的辅助函数:
能否得到证明柯西中值定理的辅助函数:

学生自行求证:验证 满足罗尔定理的条件。柯西中值定理得证。
满足罗尔定理的条件。柯西中值定理得证。
3.2. 定理的几何和物理意义 [7] - [10]
拉格朗日中值定理的几何意义:
若在一条连续的曲线弧上,除端点外处处都有不垂直于横轴的切线,则在这段曲线弧上至少有一点,使得曲线过该点的切线平行于弦AB。
拉格朗日中值定理的物理意义:
设 是质点的运动规律,则质点在时间
是质点的运动规律,则质点在时间 上走过的路程为
上走过的路程为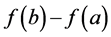 ,在
,在 上的平均速度为
上的平均速度为 ,则存在
,则存在 的某一时刻
的某一时刻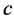 ,满足质点在
,满足质点在 时刻的瞬时速度正好是它的平均速度。
时刻的瞬时速度正好是它的平均速度。
4. 结束语
启发式教学的模式和途径是多种多样的。在教学过程中,我们应该根据实际需要有的放矢、灵活应用。通过合理、巧妙的课堂提问,做到无疑处觅有疑,有疑之处求新知,以达到激活思维、化未知为已知。
微分中值定理在微分学中的基础性作用决定了学生必须掌握并熟练应用。本文希望能为初学者理清思路,掌握微分中值定理的本质,为研究与微分中值定理有关的进一步的数学理论问题,和应用微分中值定理解决其它领域的实际问题打下坚实的基础。
基金项目
国家自然科学基金:11301224。