摘要: 让G表示一个简单连通图,图G的总离心率
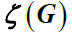
及多项式
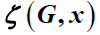
分别定义为
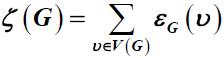
,
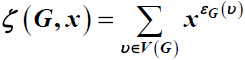
,这里
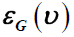
是顶点ν在G中的离心率。在本文中,计算了在图运算下图的双覆盖图和拓展双覆盖图以及剖分图的总离心率及多项式,并给出具体的关系表达式和一些界。
Abstract:
Let G be a simple connected graph. The total eccentricity
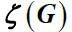
and total eccentricity polynomial
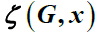
of a graph G are defined as
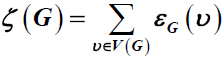
and
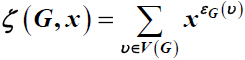
, where
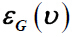
denotes the eccentricity of vertex ν in
G. In this paper, the total eccentricity and total eccentricity polynomial of double cover graph and extended double cover graph and subdivision graph of a given graph under the graph operations are computed and the exact expressions and some bounds are given.