1. 引言
基于空间分数阶偏微分方程(Space Fractional Partial Differential Equations)的图像去噪是一门崭新的交叉学科分支,而相比于整数阶偏微分方程,空间分数阶偏微分方程在图像去噪方面有更强大的生命力。
迄今为止,国内外许多学者已经建立了大量经典的基于整数阶PDE的图像去噪模型,但是许多学者在深入研究的过程中仍然发现整数阶PDE图像去噪模型存在很多不足之处。为了解决各种整数阶偏微分方程图像去噪模型存在的问题,有学者提出将分数阶微积分理论引入到偏微分方程图像去噪模型中,构建基于分数阶偏微分方程的图像去噪模型。其中Bai jian等人[1] [2] 以ROF去噪模型为基础,将分数阶微积分理论和偏微分方程相结合,提出了基于分数阶偏微分方程的图像去噪模型,该方法可以解决传统低阶次整数阶偏微分方程去噪模型容易产生阶梯效应,以及高阶次整数阶偏微分方程去噪模型去噪效果不佳的缺点。上述分数阶去噪模型的构造是利用分数阶导数来作为一种刻画图像的测度,然后根据变分法的相关理论及性质而得到相应能量泛函的Euler-Lagrange方程。
目前,将偏微分方程的图像去噪算子与其他的经典算子相结合的复合算法备受关注,张军等人 [3] 将负指数Sobolev空间的多尺度图像建模与基于分数阶微积分的图像建模有效结合,提出了统一的基于分数阶多尺度变分图像去噪模型,并初步设计了该模型涉及参数的自适应选择方法。吴亚东等人 [4] 提出利用图像分割最小化技术求解整体变分图像去噪模型,与经典梯度下降法相比,获得了较优的复原效果,但是这种方法构造复杂,在求解过程中,需要占用大量内存,耗费的运算时间非常巨大。针对这一缺点,Wu [5] 提出了一种基于交换移动空间的整体变分图像去噪算法,能够根据噪声图像局部特征自适应设定正则化参数,充分利用图像的先验知识。王嘉等人 [6] 利用神经网络求解整体变分图像去噪模型,与经典梯度下降法相比,具有收敛快速,在去除模糊的同时保持图像边缘,提高图像恢复的视觉效果等优点。王彪 [7] 等人将小波國值函数的取法移植到偏微分扩散模型的收缩系数构造中,通过正则化的桥梁将两者的思想统一到一个模型中,得到更好的处理结果。朱立新等人 [8] 引入梯度保真项来去除图像的噪声,有效的抑制了图像的阶梯效应。黄果、蒲亦非等人 [9] - [11] 认为,选择适当阶次的分数阶微分算子在图像去噪过程中可以在大幅提升边缘和纹理细节的同时,还能非线性地保留图像平滑区域的纹理信息。
然而,传统的整数阶偏微分方程去噪方法有很多局限性,现今对图像去噪的分数阶偏微分方程有限差分方法的研究和应用还很少。针对现有问题,我们对空间分数阶偏微分方程全变分去噪模型构造隐式差分格式,分析格式解的存在唯一性、稳定性和收敛性;最后,用数值试验验证隐式差分方法对于求解空间偏微分方程的有效性和优越性。
2. 空间分数阶偏微分方程图像去噪模型的隐式差分格式
2.1. 空间分数阶偏微分方程图像去噪模型
根据文献 [1] ,一种重要的整体变分图像去噪模型如下:
 (1)
(1)
上式中,第一项为残差,主要是为了保证所恢复出的图像 能够保留噪声图像
能够保留噪声图像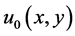 的主要特征,防止图像失真;第二项为正则项,作用是为了除去图像中噪声,在恢复图像的光滑的同时尽可能的保留图像的纹理细节信息。
的主要特征,防止图像失真;第二项为正则项,作用是为了除去图像中噪声,在恢复图像的光滑的同时尽可能的保留图像的纹理细节信息。
式(1)可以转化成求解下面方程
 (2)
(2)
式中 为时间步长,
为时间步长, 。
。
考虑(2)的初边值条件,有
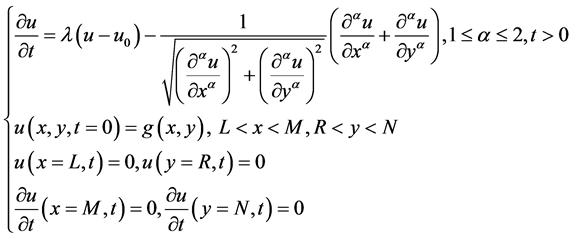 (3)
(3)
为避免数值求解的不稳定,一般用正则化梯度模值
 代替
代替 ,
,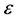 为极小量(
为极小量( 根据不同的初值选定)。
根据不同的初值选定)。
进一步化简:
当N为符号距离函数时,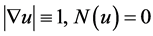 ,而且即使稍微偏离符号距离函数,N也是一个极小量,尽管
,而且即使稍微偏离符号距离函数,N也是一个极小量,尽管 是一个非线性算子,但当时间步长足够小(
是一个非线性算子,但当时间步长足够小(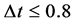 时),
时), 作用的效果可以忽略 [12] 。
作用的效果可以忽略 [12] 。
由此,(3)化简为:
 (4)
(4)
2.2. 隐式差分格式的构造
以空间步长 和时间步长
和时间步长 将求解区域划分为网格,网格点为
将求解区域划分为网格,网格点为 ,
,
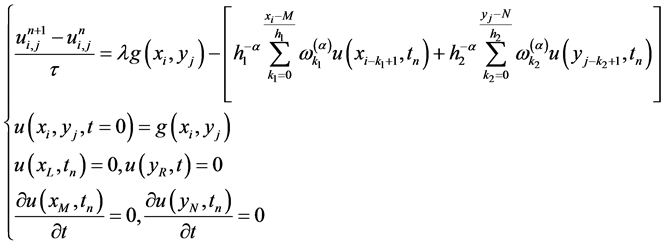 (5)
(5)
其中, 为采用基于修正的Grünwald-Letnikov逼近公式得到,且
为采用基于修正的Grünwald-Letnikov逼近公式得到,且 ,
,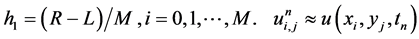 。
。
 同理。
同理。
3. 隐式差分格式解的存在唯一性
记
则格式(5)有

矩阵形式为:
 (6)
(6)
令
 ,
, ,
,
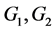 均为下三角矩阵。
均为下三角矩阵。
进一步化简得:
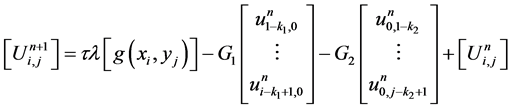 (7)
(7)
由式(7),右边n层其系数矩阵 均为下三角阵,故格式的解是存在且唯一的。
均为下三角阵,故格式的解是存在且唯一的。
综上分析,有如下定理
定理1:基于空间分数阶偏微分方程(3)的隐式差分格式(5)的解存在且唯一。
4. 隐式差分格式解的稳定性与收敛性分析及精度分析
一般情况下,Grünwald-Letnikov分数阶导数表述为
 (8)
(8)
为分析隐式格式(5)的稳定性,需要如下引理。
引理1 [13] [14] :假设 ,
, ,
, ,
,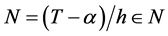 ,则有限Grünwald-Let- nikov分数阶微分算子
,则有限Grünwald-Let- nikov分数阶微分算子

为Riemann-Liouville分数阶微分算子 的一阶逼近的充分必要条件是
的一阶逼近的充分必要条件是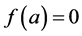 ,即
,即
 。
。
而当 时,则有
时,则有
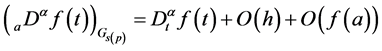 。
。
由引理1知格式(5)逼近的精度为 且满足连续,于是有
且满足连续,于是有
定理2:基于空间分数阶偏微分方程(3)的隐式差分格式(5)的精度为 。
。
设 为差分格式(5)的解,
为差分格式(5)的解,
记
则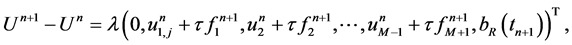
 ,
,
而 ,
,
当 时,
时,
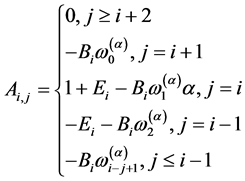 (9)
(9)
设 为A的特征值,X为对应的特征向量,即满足
为A的特征值,X为对应的特征向量,即满足 ,
,
取i,使得
又由
 (10)
(10)
若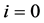 或者
或者 ,则
,则 ;
;
否则,将式(10)代入式(9),得到:

所以 ,A可逆。
,A可逆。
设 特征值为
特征值为 ,
, ,所以
,所以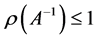 。
。
所以隐式格式(5)无条件稳定。
因此有
定理3:基于空间分数阶偏微分方程(3)的隐式差分格式(5)是无条件稳定的。
再由Lax等价定理 [14] ,有如下推论:
推论1:基于空间分数阶偏微分方程(3)的隐式差分格式(5)是收敛的。
5. 数值试验
基于Pentium(R) Dual Core CPU 3.00GHz,在Matlab7.0环境下进行数值试验。
为便于比较,选取文献 [1] 中的数值算例,使用本文的隐式差分格式(分别取a = 1、1.2、1.4、1.6、1.8、2)来对噪声图像去噪。
在基于本文去噪模型的隐式差分格式下,分别取阶次 为1、1.2、1.4、1.6、1.8、2,对加入标准高斯白噪声的Lena图像进行去噪处理,并与文献 [1] 中的去噪效果进行对比。试验结果如表1。
为1、1.2、1.4、1.6、1.8、2,对加入标准高斯白噪声的Lena图像进行去噪处理,并与文献 [1] 中的去噪效果进行对比。试验结果如表1。
由表1可看出,在相同的阶次下,本文的去噪方法得到的信噪比SNR值要比文献 [1] 所用方法得到的SNR值高,说明本文方法去噪效果较其优秀;其次,在阶次为1.6附近时,隐式差分方法所得的信噪比值较高,说明阶次在1.6附近的去噪效果较好。
本文方法与文献 [1] 方法(分数阶微分掩模算法)在阶次 分别为1.0、1.2、1.4、1.6、1.8、2.0时的去噪效果对比图如图1。
分别为1.0、1.2、1.4、1.6、1.8、2.0时的去噪效果对比图如图1。

Table 1. SNR comparison between fractional differential mask algorithm and implicit difference method
表1. 文献 [1] 方法(分数阶微分掩模算法)与本文方法(隐式差分)信噪比对比表

Figure 1. Comparison of results from different order between two methods
图1. Lena噪声图像在不同阶次下两种方法的去噪效果对比图
6. 结论
本文给出了含有初边值条件的空间分数阶偏微分方程(1)的隐式差分格式,理论分析表明隐式差分格式是绝对稳定的。数值试验的结果表明隐式差分格式的去噪效果较好,说明求解空间分数阶偏微分方程的隐式差分数值方法对于图像去噪是可行的,且效果优于分数阶微分掩模算法的图像去噪方法。
基金项目
国家自然科学基金(NO.11371135)。
*通讯作者。