1. 引言
数据聚类是把给定的数据集划分为多个类的无监督的过程,使得同一类内的数据点比不同类间的数据点更相似。在对高维空间中的数据集聚类时,许多算法的有效性和效率会明显降低。主要有以下几个原因,一是高维数据的内部稀疏性阻碍了这些算法性能的发挥;二是高维空间中两点距离趋于一致 [1] ,因此从不相似数据中找出相似数据的难度更大;三是高维空间中的类可能存在于子空间中,不同的类可能存在于不同的子空间中 [2] 。图像聚类是典型的高维空间聚类,因为几乎所有图像特征的维数都很高。因此,高维聚类的难题也存在于图像聚类中。虽然近年来出现了不少聚类算法,但他们中的许多算法在对图像聚类尤其是图像视觉聚类中的效果并不好。在视觉聚类中经常使用的仍然是k-means算法,这或许是因为设计一个能替代k-means的通用聚类算法确实比较困难。但是,在增量数据集上,k-means的缺点会比较明显,因为它的聚类速度很慢,而且不支持增量聚类,运行时间会随着数据集规模的增大而急剧增长。在用于视觉词典生成的聚类中存在着多义性和同义性等问题,这就需要找出新算法。
随机映射是近年来研究较多的算法,它可以降低维数同时在一定程度上保持原有结构不变。例如,欧式空间的n维的点可以映射到d维并且d远小于n。这样的随机映射主要应用在降维 [3] 和快速近似最近邻搜索 [4] ,它的应用范围还包括信号处理 [5] 、异常检测 [6] 、聚类 [7] 和分类等 [8] [9] 。
E2LSH (Exact Euclidean Locality Sensitive Hashing) [10] 是随机映射的一个特例,近年来也引起了人们更多的注意,被应用在不少领域如检索 [11] 、复制检测 [12] 等。它在用于近似最近邻检索时,在保持较高准确率的同时有着很低的运行时间,是当前近似最近邻检索的主流算法。它把高维向量映射到低维空间后,也完成了维数约减的任务。同时,相同的桶中的点比不同桶中的点更相似。因此,如果根据桶标志对数据点进行分组,也可以达到对数据点进行聚类的目的。而且,E2LSH是一个数据无关的方法,它在对一个点进行映射时与其它点无关,这意味着它可以方便地为一个动态数据库建立索引。类似地,用于聚类时,当数据集规模变化时不需要对整个数据集重新进行聚类,只需要对变化的数据点运算即可,也就是说它可以方便地起到动态聚类的作用,再加上它的时间优势使得它可以较好的用于增量大数据集聚类。事实上,LSH算法的提出者已经指出LSH可以用于快速聚类,但他没有进一步进行理论证明和实验验证。不过,Ravichandran D已经将LSH的欧式空间实现方案E2LSH用于名词聚类 [13] 。然而,图像数据比文本数据要复杂得多,因此,对图像进行聚类也比对名词进行聚类要困难的多。
为解决k-means算法在图像聚类中的问题,提出了集成式位置敏感聚类方法(ELSC, Ensemble based Locality Sensitive Clustering),该方法基于E2LSH算法和聚类集成算法。它同时利用了E2LSH和聚类集成的优点,这使得它可能成为有效的聚类方法。其中基于E2LSH的聚类称为位置敏感聚类,它的可行性来自于随即映射的距离保持特性和可分性保持特性。
2. 位置敏感聚类可行性
随机映射在模式识别和数据挖掘中的主要作用是降维。除了降维之外,随机映射还可用于聚类。聚类的基础在于它对数据集可分性的保持。这里的可分性保持主要涉及距离保持和边界保持。对于数据聚类,Johnson-Lindenstrauss定理说明经过映射数据点间的距离以很高的概率得以保持。这是信息检索中近似最近邻搜索算法的基础。
2.1. 随即映射的距离保持和边界保持特性
Johnson-Lindenstrauss定理说明了映射的距离保持性质。给定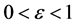 和数据集
和数据集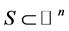 ,对于正整数
,对于正整数 ,存在一个映射
,存在一个映射 ,使得对于所有
,使得对于所有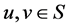 ,
,
 (1)
(1)
该定理说明,映射后成对数据点的距离有很大的可能性被以 为倍数保留下来。对于高维空间
为倍数保留下来。对于高维空间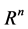 中的数据集S,假设随机地把数据映射到
中的数据集S,假设随机地把数据映射到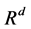 ,映射后的维数
,映射后的维数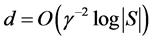 足够以较高的概率使数据点间的角度最多改变
足够以较高的概率使数据点间的角度最多改变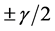 [14] 。特殊地,如果把S中所有数据点映射到向量
[14] 。特殊地,如果把S中所有数据点映射到向量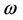 ,如果原始数据以边界
,如果原始数据以边界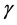 可分,那么映射后,角度改变最大为
可分,那么映射后,角度改变最大为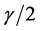 ,数据点仍然可分。
,数据点仍然可分。
分类中边界保持也可为聚类提供有效信息。文献 [15] 建立了随机映射后边界保持的条件,并说明如果该条件满足,无差错边界在二分类和多分类问题中能被保持。文献 [8] 研究了二分类随机映射的边界保持问题,并给出了随机映射以给定概率保持原始数据一半的边界所需要维数的下界,但它需要无限多维数才能保持无差错边界。如果原始数据有归一化边界 ,那么只有映射数目
,那么只有映射数目
 (2)
(2)
时,对任何合适的常量c,映射后的数据以大于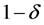 的概率以错误
的概率以错误 有边界
有边界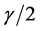 。
。
二进制边界保持的内容为:给定任意的随机高斯矩阵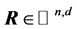 ,如果数据集
,如果数据集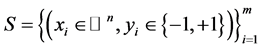 是被边界
是被边界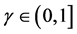 线性可分的,那么对任何
线性可分的,那么对任何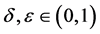 和任何
和任何
 (3)
(3)
情况,数据集 以至少
以至少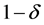 的概率被边界
的概率被边界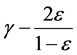 线性可分。
线性可分。
随机映射后边界的下界对某些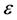 可能变为负值。负边界意味着映射后的数据不是线性可分的。当边界为正时,上式说明二进制分类中的边界经过随机映射后以很高的概率得以保持。
可能变为负值。负边界意味着映射后的数据不是线性可分的。当边界为正时,上式说明二进制分类中的边界经过随机映射后以很高的概率得以保持。
多类无差错边界保持的内容为:对于归一化边界,如果存在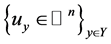 对所有
对所有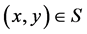 ,使得
,使得
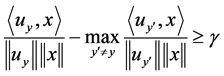 (4)
(4)
那么,多类数据集 是被边界
是被边界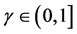 线性可分的。
线性可分的。
多类边界保持的问题如下:对任何多类数据集S和任何高斯随机矩阵R,如果S是被边界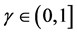 线性可分的,那么对任何
线性可分的,那么对任何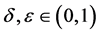 和任何
和任何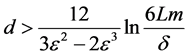 情况,数据集
情况,数据集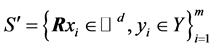 以至少
以至少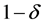 的概率是被边界
的概率是被边界 线性可分的。
线性可分的。
2.2. 位置敏感聚类
E2LSH是LSH (Locality Sensitive Hashing)的欧式空间实现方式,是一种基于随机映射的方法。因此以它为基础设计的算法具有对数据进行聚类的能力。位置敏感聚类的基础就是E2LSH算法的位置敏感哈希函数。该函数是基于p-稳定分布函数的, 。位置敏感哈希函数的定义为:
。位置敏感哈希函数的定义为:
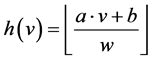
其中a是由p-稳定分布函数产生的n维随机向量,内积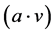 对数据点进行随机映射,b对映射后的结果加上一个偏移,取模运算确保映射后的哈希值(桶标记)在一定范围内。可见,哈希函数的生成要用随机的方法,内积运算对数据点进行映射。但E2LSH与一般的随机映射不同,它使得数据点映射后不在随机向量所在方向的全坐标轴上,而是映射到了坐标轴的一部分。另外一个不同在于映射运算,一般的随机映射需要构造随机映射矩阵并进行矩阵运算,也就是每个点都要与一个矩阵进行运算。但E2LSH中,每个点只需要进行内积计算,这可以降低内存消耗和计算复杂度。
对数据点进行随机映射,b对映射后的结果加上一个偏移,取模运算确保映射后的哈希值(桶标记)在一定范围内。可见,哈希函数的生成要用随机的方法,内积运算对数据点进行映射。但E2LSH与一般的随机映射不同,它使得数据点映射后不在随机向量所在方向的全坐标轴上,而是映射到了坐标轴的一部分。另外一个不同在于映射运算,一般的随机映射需要构造随机映射矩阵并进行矩阵运算,也就是每个点都要与一个矩阵进行运算。但E2LSH中,每个点只需要进行内积计算,这可以降低内存消耗和计算复杂度。
在随机映射可分性保持的基础上,一个数据集在经过位置敏感哈希函数映射后,相对距离和类边界能够得以保持。这为E2LSH用于聚类提供了可行性经过映射后,桶标记相同的点比桶标记不同的点相似度高,而且桶标记相邻的点也比桶标记不相邻的点的相似度高。因此,可以利用桶标记对数据点进行分组,也就是把桶标记相同或相邻的数据点分为一类。这种以E2LSH的位置敏感哈希函数为基础的聚类方法就是位置敏感聚类(LSC, Locality Sensitive Clustering)方法。
3. 集成式位置敏感聚类
集成式位置敏感聚类方法(Ensemble LSC)的基础是位置敏感聚类和聚类集成。聚类集成是集成学习的一部分,是近年机器学习领域的研究热点之一。聚类集成对改善聚类性能有着重要的作用,这是因为没有一个单一的聚类算法能够发现不同形状和不同分布的类,而不同数据集的内部结构是不同的。聚类集成同一数据集的多个基聚类方案结合起来,得出一个统一的聚类方案,该方案比大多数基聚类方案的聚类质量要好。聚类集成与集成学习的另一个研究方向——分类融合类似,分类融和可以将分类器用bagging、boosting融合起来,也可以将分类器的结果进行融合。然而,聚类集成更具挑战性。首先,不同基聚类器得出的聚类数目可能不同,其次,聚类标签只是一个标记符号,继承以前需要解决不同聚类方案的标签对应问题。第三,集成器无法获取原始数据,只能访问基聚类的类标签。使用聚类集成的原因和优势主要在于 [16] :改善聚类质量,提供稳健聚类方法,提供模型选择问题新方法,知识复用,多角度聚类,分布计算。
3.1. 聚类集成框架
聚类集成方法主要由两步组成:生成多个基聚类划分,即用基聚类算法对数据集创建多个划分;生成最终划分,即对基聚类得出的划分进行合成得出一个新的划分。Topchy等证明 [17] ,只要采用合适的一致函数(Consensus Function),弱聚类算法能够产生高质量的集成聚类。用于产生基聚类划分的一致函数有多种,这里采用如下的三种方法。
基于聚类的相似划分算法(Cluster-based Similarity Partitioning Algorithm, CSPA) [16] 首先创建一个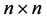 相似矩阵,n是数据集X的对象的个数,这可以看作全连接图的邻接矩阵,图的节点表示数据集的对象,两点间的边是一个相关权值,其值等于同一类中这两个对象出现在同一类中的次数。超图划分算法(Hyper-Graph Partitioning Algorithm, HGPA) [18] 创建一个超图,节点代表对象,相同权值的超边代表类。然后用HMETIS将该超图划分为大致相等的k部分。元聚类算法(Meta-CLustering Algorithm, MCLA)生成的图表示类间的关系,节点对应于各个类,每个边的权值用二进制Jaccard相似度计算。然后使用METIS把该图划分为k个元类。最后通过将每个对象分配给关联最多的元类得出最终划分。
相似矩阵,n是数据集X的对象的个数,这可以看作全连接图的邻接矩阵,图的节点表示数据集的对象,两点间的边是一个相关权值,其值等于同一类中这两个对象出现在同一类中的次数。超图划分算法(Hyper-Graph Partitioning Algorithm, HGPA) [18] 创建一个超图,节点代表对象,相同权值的超边代表类。然后用HMETIS将该超图划分为大致相等的k部分。元聚类算法(Meta-CLustering Algorithm, MCLA)生成的图表示类间的关系,节点对应于各个类,每个边的权值用二进制Jaccard相似度计算。然后使用METIS把该图划分为k个元类。最后通过将每个对象分配给关联最多的元类得出最终划分。
Strehl和Ghosh把一致划分(即最终划分)定义为与各个基聚类器得出的划分共享信息最多的划分 [19] ,为测量两个划分共享的信息量,他们定义了基于信息论中互信息的归一化互信息(Normalized Mutual Information, NMI),用来度量两个划分相似度。用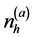 表示划分
表示划分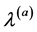 类
类 中数据点的个数,
中数据点的个数,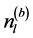 表示划分
表示划分 中类
中类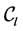 中数据点的个数,
中数据点的个数,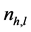 表示同时在这两个类中点的数目。那么,NMI的定义为:
表示同时在这两个类中点的数目。那么,NMI的定义为:
 (6)
(6)
其中 和
和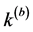 分别表示两个划分的类的个数。NMI的最大值为1最小值为0。
分别表示两个划分的类的个数。NMI的最大值为1最小值为0。
在此基础上,一致划分就是和所有基划分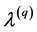 有最大平均互信息的划分:
有最大平均互信息的划分:
 (7)
(7)
其中 是所有可能的m个划分中的一个。这里也采用这种方法进行最终划分。
是所有可能的m个划分中的一个。这里也采用这种方法进行最终划分。
3.2. 集成式位置敏感聚类
由于位置敏感聚类存在一定的随机性,提出集成式位置敏感聚类的方法来改善聚类质量。集成式位置敏感聚类是位置敏感聚类和聚类集成的合成。主要包括三部分,确定聚类数目,生成多重位置敏感聚类方案,多个聚类方案集成。这里我们采用事先指定聚类数目的方式。有了聚类数目以后,就可以生成多个基聚类并进行集成。ELSC的完整过程如下:
1) 为数据集S确定聚类数目k;
2) 生成服从高斯分布的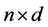 的随机矩阵
的随机矩阵 和b、w,
和b、w,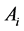 是一个d维向量,
是一个d维向量,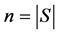 ;
;
3) 对所有数据点 进行随机映射,每个点
进行随机映射,每个点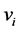 的映射的结果为d维桶标记
的映射的结果为d维桶标记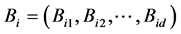 ,
,
 (8)
(8)
这样,全部数据点的桶标记就是一个 维矩阵
维矩阵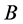 。
。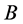 的每一列都是对全部数据集的一次映射。
的每一列都是对全部数据集的一次映射。
4) 用PAM算法对 的每一列聚成k类,得出的结果即对数据集的d个划分,用
的每一列聚成k类,得出的结果即对数据集的d个划分,用 表示。
表示。
5) 使用聚类集成方法对d个基划分进行集成并得出最终划分。采用的聚类集成方法包括CSPA、HGPA和MCLA,它们各自得出一个集成划分,记作 ,最终划分是和其它两个划分有最大归一化互信息的划分,即
,最终划分是和其它两个划分有最大归一化互信息的划分,即
 (9)
(9)
4. 实验
为直观地看到聚类结果,首先在人工数据集上进行试验。人工数据集有两个,一个包括30个2维的数据点(记作“数据集1”),依次属于3个类,每个类10个点,前10个点属于第一类,最后10个点属于第3类。另外一个数据集包括30个100维的数据点(记作“数据集2”),同样依次属于3个类。此外,为验证在实际数据上的聚类结果,构造了一个图像集(记作“图像集1”),该图像集从TRECVID数据集选取,包括4类75幅图像,每类选取部分图像,这些图像也依次分别属于4个类,这4个类是“compere”、“singer”、“rice”和“sports”。实验测试环境为8G DDR3 1600 RAM和AMD速龙II X2 255双核主频3.11 GHz CPU,操作系统为Windows 7 64位旗舰版,开发环境为Matlab 2013a和Visual Studio 2010及相关开发包。
4.1. 人工数据集实验
首先在人工数据集1上进行比较,由于ELSC是基于聚类集成的算法,将它与基于聚类集成的k-means算法(记作“Ek-means”)进行比较。K-means算法的基本思想是:以空间中k个点为中心进行聚类,对最靠近他们的对象归类。通过迭代的方法,逐次更新各聚类中心的值,直至得到最好的聚类结果。k-means聚类如图1所示。
由图1可见,所有30个点被正确地分为3个类。将该实验重复多次,其中5次聚类结果如表1所示,表中仅给出了第1类数据的类标签。可见,虽然每次得出的类标签不同,但这些标签都是正确的,因为它们都把这些点聚到了一类。在这些类标签上运行聚类集成算法后,Ek-means得出完全正确的结果,最终类标签为[1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3]。
对数据集1运行ELSC算法,其桶标记计算结果见图2所示。桶标记是由位置敏感哈希函数对数据点映射后得出的。将该实验重复多次,其中5次的桶标记如表2所示。
从表2可见,每个聚类结果中同一个类的每个点的桶标记不同,但每个类类内桶标记都在较小的范围内波动。由图2可知,类内两点桶标记的距离小于类间两点桶标记的距离。不同聚类结果中同一个点的桶标记也可能不同,这与哈希函数中的随机性有关。
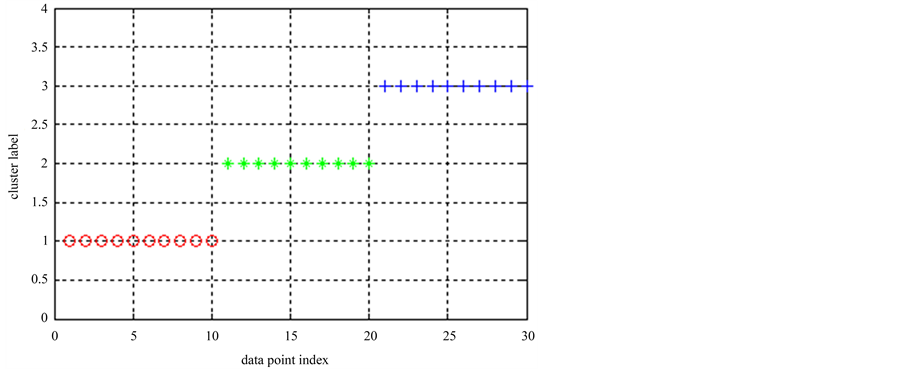
Figure 1. k-means clustering result in data set 1
图1. 数据集1上k-means聚类结果
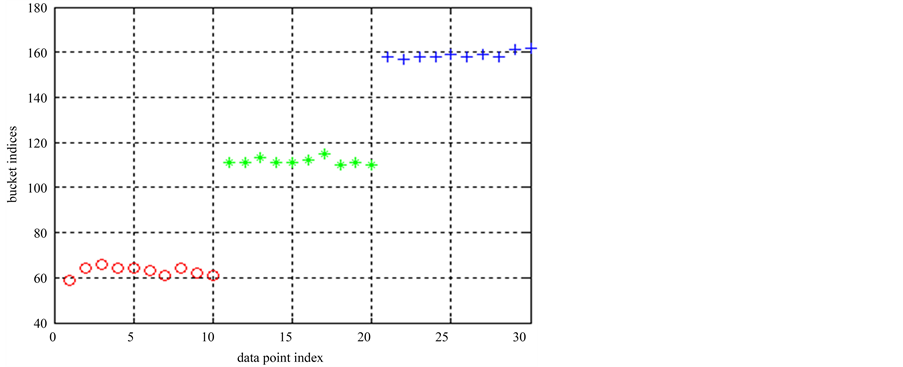
Figure 2. ELSC bucket number result in data set 1
图2. 数据集1的ELSC桶标记计算结果

Table 1. The label of k-means clustering from the first type in data set 1
表1. 数据集1第1类数据k-means聚类得出的类标签

Table 2. The bucket indices of ELSC algorithm from the first type in data set 1
表2. 数据集1第1类数据的ELSC桶标记计算结果
对这些桶标记进行运算,可得出数据集1的多个基划分。采用PAM算法对基划分进行聚类,并运行聚类集成算法,得出的最终划分的类标签是[1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3],这与Ek-means的结果相同。
为验证新的聚类算法在高维数据上的运行效果,在数据集2上也进行了实验。先运行了k-means算法,其聚类结果如图3所示,图中所有30个数据点被正确地分为3类。重复该实验多次,对这些聚类结果进行集成后,Ek-means可得出完全正确的结果。最终的类标签是[1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3]。
在数据集2上运行ELSC算法,得出的桶标记如图4所示,桶标记正确地反映了对应点所属的类别信息。对这些桶标记进行PAM聚类以产生多个基划分。并运行聚类集成算法,最终划分的类标签为
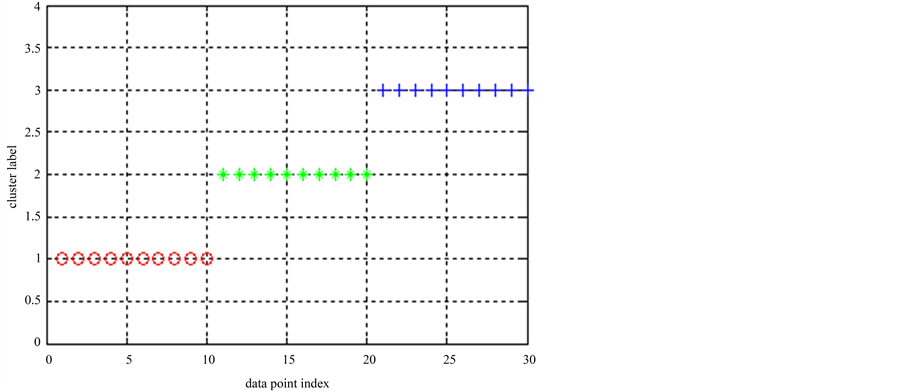
Figure 3. k-means clustering result in data set 2
图3. 数据集2的k-means聚类结果
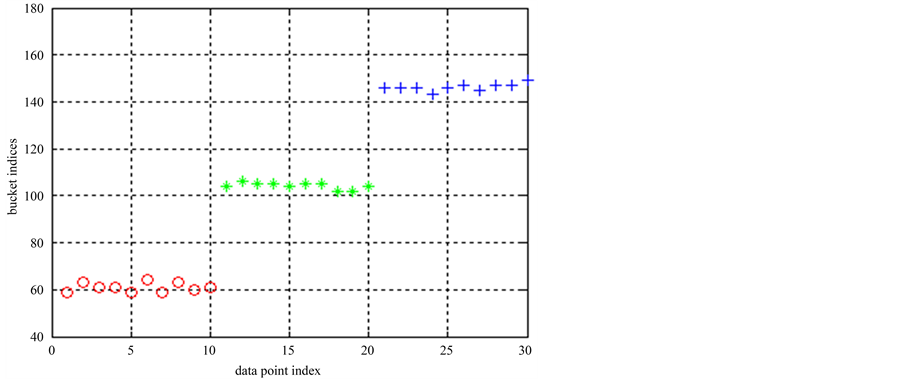
Figure 4. ELSC clustering result in data set 2
图4. 数据集2的ELSC算法的桶标记
[1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3]。该结果也与Ek-means相同。
这些实验说明,在人工数据集上,ELSC可达到与Ek-means相同的准确率。
4.2. 图像集实验
在图像集1上运行k-means结合聚类集成(记作“EKM”)和ELSC算法进行比较。先运行k-means算法,其结果如图5所示。然后重复多次,得出多个基划分(或基聚类),再在基划分的基础上运行聚类集成算法,最终划分的类标记为[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4]。可见,虽然基划分存在一些错误的类标签,但EKM算法产生的最终划分是完全正确的。
图像集1的ELSC算法产生的桶标记如图6所示,第1类、第2类和第4类的桶标记中部分点对应的类别信息是错误的,第3类图像的结果完全正确。多次划分中第2类图像的桶标记如表3所示。
对这些桶标记分别运行PAM聚类算法,就可以得出图像集1的多个基划分,最后运行三种聚类集成算法,得出三种集成划分,并通过互信息的衡量去最好的集成划分作为最终划分。最终划分的标签为[3 3 3 3 3 3 2 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 3 2 2 2 2 2 2 2 2 2 2 2 2 3 3]。图像集1的最终划分显示在图7中,该次试验的聚类准确率为93%。

Table 3. The bucket indices of the ELSC algorithm in the second type of images
表3. 图像集1第2类图像ELSC算法的桶标记
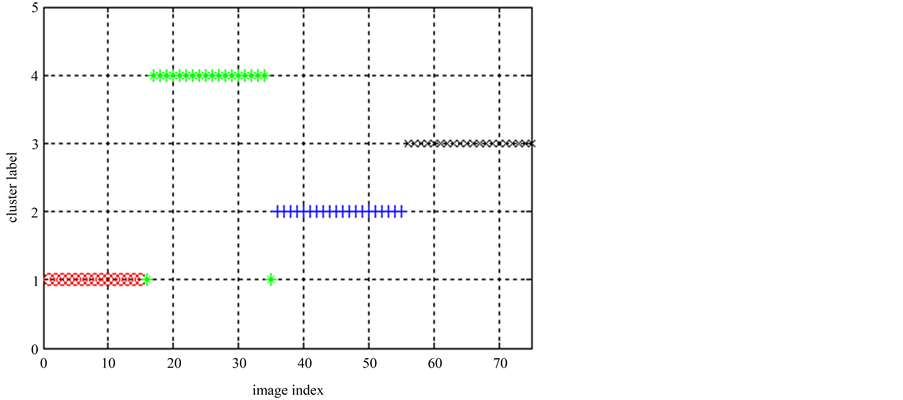
Figure 5. k-means clustering result in image set 1
图5. 图像集1的k-means聚类结果
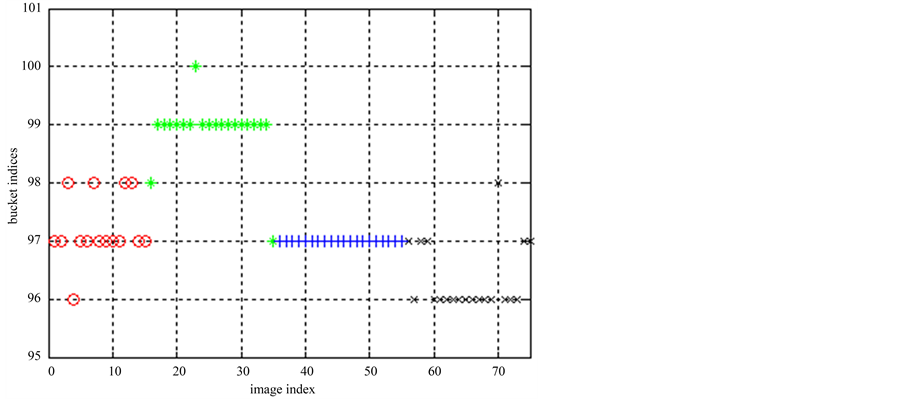
Figure 6. ELSC bucket indic result in Image 1
图6. 图像集1的ELSC算法的桶标记
为验证算法的运行时间和准确率,在图像集1上多次运行两种算法。两种算法的基划分从10增加到100,增加间隔为10,在不同数量的基划分上分别进行聚类集成,得出10个最终划分。并将该过程重复10次,将聚类时间进行平均,最终得出的聚类时间如图8所示,ELSC的运行时间要少于EKM,而且基聚类数目越大,其聚类时间的优势越大。
在准确率上,采用F值和MAP值进行比较。MAP将4个类作为整体进行计算,其结果如图9所示,可见在一些基划分上两种算法各有优势,但平均而言,它们的平均值分别为0.9667和0.9662,即ELSC仍有一定优势。F值对4个类分别计算,其值如表4所示。在各类别各划分上,两种算法各有优势,但差距不大。对不同的基划分方案进行平均,前3个类EKM略高,第4类ELSC略高。
图像集1的实验证明,ELSC算法在真实数据集上能达与EKM相当甚至稍高的准确率。而且它优势在于继承了E2LSH低内存消耗、低计算代价和短运行时间的特点,以及其自身的数据无关特性决定的对增量聚类的适应性。E2LSH的全数聚集运行时间低于该数据集规模的线性水平,数据集更新时只需要对更新数据进行计算,这都远远低于k-means的计算时间。尤其是数据更新时,k-means需要重新对全数聚
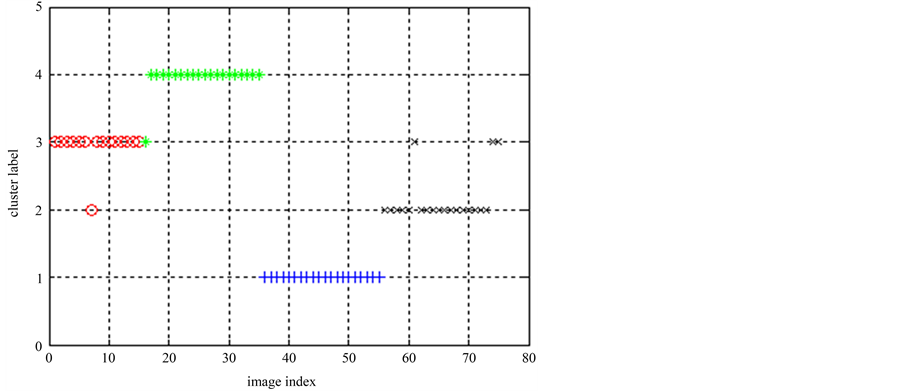
Figure 7. Class symbol of ELSC division in Image 1
图7. 图像集1 ELSC算法最终划分的类标签

Figure 8. The clustering time of two algorithms in image set 1
图8. 图像集1两种算法的聚类时间
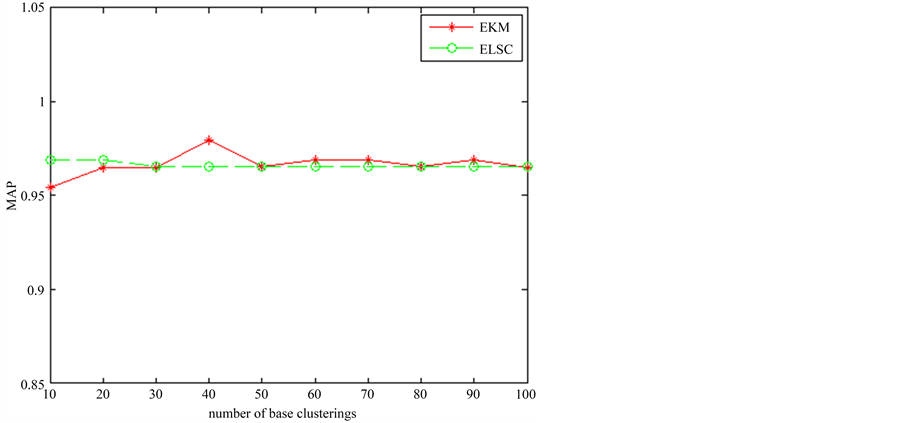
Figure 9. The MAP of ELSC in image set 1
图9. 图像集1 ELSC算法的MAP值

Table 4. The F number of the algorithms in each type of image set 1
表4. 图像集1各类别的F值
集聚类。综合准确率、时间复杂度和可增量运算几点来看,ELSC是可以用于高维空间数据聚类的。尤其是增量聚类和快速聚类对当前大数据处理是非常重要的。
5. 总结
集成式位置敏感聚类(ELSC)方法是在聚类集成和E2LSH的基础上提出的,它具有快速聚类和增量聚类的优点,随机性也比以E2LSH为基础的位置敏感聚类低。它在人工数据集和图像数据集上都表现出了较好的性能,不但聚类时间大大缩短,聚类准确率也与EKM相当。另外,它还具有内存消耗低、计算代价小等对大规模数据聚类相当重要的优点。这些决定了ELSC在大规模高维数据集聚类上将能发挥重要的作用,尤其是在图像视觉词典生成过程中的聚类算法中,ELSC将会是k-means的一个替代算法,我们下一步将深入研究ELSC如何应用于视觉词典法,在图像分类、识别和检索等任务中展开应用。
基金项目
国家自科学基金项目(编号61301232)资助。