1. 引言
归纳推理是一个从特殊实例中推断出一般规则或关系的过程,是人脑的重要的高级认知功能之一。但对其认知成分的了解还很少。虽然归纳推理存在许多不同的模型,例如相似性覆盖模型、基于特征的归纳模型、假设–评价模型、贝叶斯模型和相关理论模型等(梁佩鹏,2009),但是,这些模型都是针对类别归纳推理(Osherson等,1990)的,不适用于序列完型任务的归纳推理过程。
序列完型任务包括字母序列完型问题和数字序列完型问题(如A C E G ?和2 5 8 11 ?),是一种典型的归纳推理任务,求解时,人们需观察或总结出序列元素间的关系,并应用该关系推断出接下来的一个字母/数字(即:I和14)。字母型和数字型序列完型任务被认为具有相同的核心认知成分,尽管任务内容(字母vs.数字)会对这些成分产生影响。
Simon和Kotovsky(1963)较早对字母序列完型任务进行了研究,认为该任务的加工过程包括4种认知成分:关系检测、周期发现、模式描述及推断。以任务“a a a b b b c c c d d ?”为例,关系检测包括观察这个序列并产生一个关于相邻元素关系的假设(如:前3个元素的关系是“它们是一样的”)。周期发现包括检测周期界限和结构(如:包含4个以3个元素为周期的序列)。模式描述包括解释全部元素位置关系准则的产生,包括周期内的和周期间的(如:本任务周期内的元素关系为“它们是相同的”;周期间的元素关系为“它们按照字母表顺序依次增加”)。推断则是根据上一步得到的模式,预测接下来的元素(如:“?”位置应该填入d)。
Holzman,Pellegrino和Glaser(1983)首次将上述四种认知成分引入到数字序列完型任务中,认为数字序列与字母序列是同质的,并进一步考察了不同变量(包括工作记忆、年龄和智商等)对解决数字序列完型任务的影响。LeFevre和Bisanz(1986)进一步对数字序列完型任务中的关系检测成分进行了深入研究,并将该认知成分进一步分为3个子成分:识别(Recognition of memorized series)、计算(Calculation)、检查(Checking)。其中,识别是对视觉呈现的数列与语义记忆中提取的数列进行的一种直接的、相对较快速的比较过程(例如,“1 3 5 7”)。而当加工不熟悉的数字序列时(例如“5 11 17 23”),识别成分尝试进行语义记忆提取失败后,计算成分就会启用,以计算元素间的间隔,进而获得该序列的内部规则(即,+6)。但对于数字序列“1 3 5 6”或“7 13 19 25”,当第4个位置的异常数字不符合简单规则时,就会中断对该序列的识别或计算操作,这种异常数字可能意味着当前规则是不正确的,被试会重新加工以确认该异常数字的出现是否为错误造成(例如:数字编码错误或计算错误),这一过程成为检查。特别地,与预期元素差异较大的序列(“2 5 8 11 93”)相比,与预期元素差异较小的序列(“2 5 8 13”)引起的检查成分更明显。
近年来,眼动技术已被广泛应用于脑高级认知功能的研究中(胡中华,赵光,刘强,李红,2012;王乾东,胡超,傅根跃,2013)。注视时间、注视次数、回视次数等眼动指标能实时地反映视觉加工过程,所蕴含的信息远超过纯行为学指标(即反应时和正确率),能反映出更为精细的认知加工过程(Geyer, Von Mühlenen & Müller, 2007)。注视时间和注视次数两个指标可以在一定程度上说明实验任务的复杂程度,因为越复杂的任务,注视时间越长,相应的注视次数也就越长。如果被试不是从左向右的方向顺序阅读任务的话,视为回视,例如,当被试看到异常元素后,会去检验先前看过的元素,去检测这种差异是否由简单的编码错误或计算错误引起,从而打破从左向右的顺序,因此,回视是检查成分的重要眼动表现。Wriessnegger,Janzen和Albert(2002)将眼动技术应用到字母序列完型任务中,首次通过眼动指标定量地、客观地证实了Simon和Kotovsky(1963)提出的过程模型。
本研究的目的是利用眼动技术验证数字序列完型任务的关系检测成分中识别、计算及检查三个子成分的存在。本研究为2(序列类型:计数、非计数) × 3(规则有效性:有效、无效、异常)实验设计,通过Tobii T120眼动仪采集实验数据,分析不同任务条件的注视时间、注视次数和回视次数。计数序列通过识别成分即可完成,而非计数序列不能依靠识别成分完成,需要计算成分的参与,因此,结合上述对这些成分的定义,我们推测:与计数序列相比,非计数序列将有更长的注视时间,及可能较多的注视次数和回视次数。而由于无效任务中检查成分的存在,相比于有效任务,无效任务可能将有更多的回视次数,因而有更长的注视时间和更多的注视次数。
2. 研究方法
2.1. 被试
选取北京工业大学生被试15名(男生8人),年龄在21~26岁之间(23.7 ± 1.4),视力正常。所有被试均签署了知情同意书,并在实验后给予一定报酬。
2.2. 实验设备
本实验采用的仪器为瑞典生产的Tobii T120眼动仪,采样频率为120 Hz。实验刺激呈现于17寸彩色液晶显示器上,显示分辨率为1024 × 768。使用SPSS 19.0对实验数据进行统计分析。
2.3. 实验程序
本研究为2 × 3设计。因素一是序列类型(计数(Counting)、非计数(Non-Counting)),因素二是规则有效性(有效(True)、无效(Invalid)、异常(Anomalous))。计数(Counting)任务为平时人们很熟悉的数列(如1 2 3 4或1 3 5 7),而非计数(Non-Counting)任务则与计数(Counting)任务相对,是平时人们不熟悉的数列;有效(True)任务为具有规则有效性的数列,无效(Invalid)任务和异常(Anomalous)任务没有规则有效性。因此,本实验共有6种实验任务。其中,计数–有效(Counting-True,CT)任务是指非常熟悉且具有有效规则的数列;计数–无效(Counting-Invalid)任务是指非常熟悉但没有有效规则的数列,CI数列是通过把CT数列中某一个元素加1或减1得来;计数–异常(Counting Anomalous, CA)任务指非常熟悉但显著存在异常数字的数列,CA数列通过把CT数列中的某一元素的值替换为一个较大的异常数字得来;非计数–有效(Non-Counting True, NCT)任务是不熟悉的、具有有效规则的数列;非计数–无效(Non-Counting Invalid, NCI)任务和非计数–异常(Non-Counting Anomalous, NCA)任务也都是不熟悉的数列,但是,一个是将NCT数列中某一个元素加1或减1得来,而另一个则是将NCT数列中某一个元素替换为一个存在显著差异的异常数字。所有实验任务见表1。
2.4. 实验过程
所有刺激均为图片形式呈现。被试坐在距离屏幕65 cm处的椅子上,主试对其进行头矫正和眼矫正。正式实验开始前,被试先进行练习,练习任务不包含在正式任务中。实验中,所有任务呈现是随机的,但同时保证没有3个规则有效的任务或者3个规则无效的(无效和异常)的任务连续出现。实验任务将一直呈现在屏幕上,直到被试按键作答,然后跳转到下一题目。实验过程中,要求被试尽可能快并准确地判断屏幕上出现的数列是否可以由一种简单的规则所描述。若可以,则用左/右手食指按键作答;若不可以,则用右/左手食指按键作答。按键反应被试内平衡。眼动仪将记录所有眼动数据和被试的按键反应。
2.5. 兴趣区划分
本研究中,刺激被划分为4个兴趣区(AOI, area of interest),分别与任务中每个数字的位置相对应

Table 1. Experimental task
表1. 实验任务
(AOI-1、AOI-2、AOI-3、AOI-4分别对应任务中第1个、第2个、第3个、第4个数字),划分的兴趣区用来描述被试完成任务时的眼动指标。
3. 结果
3.1. 正确率
6种条件下被试均获得较高的正确率:CT(0.981 ± 0.073)、NCT(0.948 ± 0.111)、CI(0.955 ± 0.134)、NCI(0.940 ± 0.147、CA(1 ± 0)、NCA(0.977 ± 0.084),且没有显著差异。这可能是由于实验任务均比较容易,因而出现了天花板效应。
3.2. 注视时间
结果如图1所示。序列类型主效应显著(F (1, 14) = 32.368, p < .001),规则有效性主效应显著(F (2, 28) = 31.943, p < .001),序列类型和规则有效性的交互效应显著(F (2, 28) = 5.141, p = .013)。
进一步的简单效应分析发现:NCT、NCI、NCA的注视时间分别显著长于CT(F (1, 14) = 33.366, p < .001)、CI(F (1, 14) = 7.860, p = .014)和CA(F (1, 14) = 8.018, p = .013)。
另外,对于计数序列任务,CI的注视时间显著长于CT(F (1, 14) = 25.842, p < .001)和CA(F (1, 14) = 31.117, p < .001),且CT的注视时间也显著长于CA(F (1, 14) = 10.565, p = .006)。对于非计数序列任务,NCI的注视时间显著长于NCT(F (1, 14) = 17.543, p < .001)和NCA(F (1, 14) = 40.367, p < .001),且NCT的注视时间显著长于NCA(F (1, 14) = 14.329, p < .002)。
3.3. 注视次数
结果如图2所示。序列类型主效应显著(F (1, 14) = 21.248, p < .001),规则有效性主效应显著(F (2, 28) = 15.312, p < .001),序列类型和规则有效性的交互效应边缘显著(F (2, 28) = 3.008, p = .066)。
进一步简单效应分析发现,NCT、NCI、NCA的注视次数分别显著/或边缘显著多于CT(F (1, 14) = 28.001, p < .001)、CI(F (1, 14) = 3.216, p = .095)和CA(F (1, 14) = 4.629, p = .05)。
另外,对于计数序列任务,CI的注视次数显著多于CT(F (1, 14) = 14.480, p = .01)和CA(F (1, 14) = 18.972, p < .001),且CT的注视次数也显著多于CA(F (1, 14) = 9.124, p = .01)。对于非计数序列任务,NCI的注视次数接近显著多于NCT(F (1, 14) = 4.086, p = .063),显著多于NCA(F (1, 14) = 11.483, p = .01),且NCT的注视次数显著多于NCA(F (1, 14) = 14.209, p = .01)。
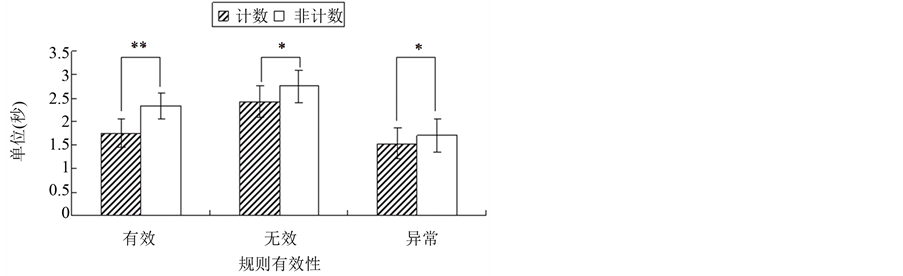
Figure 1. The fixation duration
图中**表示p < .005,*表示p <.05。
图1. 注视时间

Figure 2. The fixation count
图中**表示p < .005,*表示p < .05。
图2. 注视次数
3.4. 回视次数
本研究将任务划分为4个AOI,因此本研究中的回视指的是注视点在各个兴趣区之间的转换,回视次数为所有转换次数的和。回视次数结果如图3所示。
序列类型主效应显著(F (1, 14) = 17.988, p < .001),规则有效性主效应显著(F (2, 28) = 21.422, p < .001),序列类型和规则有效性的交互效应不显著(F (2, 28) = 2.185, p = .131)。
进一步简单效应分析发现,NCT、NCA的回视次数分别显著多于CT(F (1, 14) = 16.633, p < .001)、和CA(F (1, 14) = 8.459, p = .05)。尽管NCI与CI的回视次数没有达到显著(F (1, 14) = 2.456, p = .139),但NCI的回视次数呈现多于CI的趋势。
另外,对于计数序列任务,CI的回视次数显著多于CT(F (1, 14) = 8.279, p = .05)和CA(F (1, 14) = 28.491, p < .001),且CT的回视次数也显著多于CA(F (1, 14) = 21.888, p < .001)。对于非计数序列任务,NCI的回视次数接近显著多于NCT(F (1, 14) = 3.660, p = .076),显著多于NCA(F (1, 14) = 16.840, p < .001),且NCT的回视次数显著多于NCA(F (1, 14) = 18.959, p < .001)。
4. 讨论
本研究首次通过注视时间、注视次数和回视次数这三种眼动测量,证实了数字归纳推理中的识别、计算和检查3个认知子成分的存在,这些证据比反应时和正确率更为客观。
4.1. 识别成分和计算成分
不论根据注视时间、注视次数,还是回视次数,计数序列均短于或少于非计数序列(CT < NCT,CI < NCI,CA < NCA;尽管对于回视次数,CI和NCI的差异并不显著,但是从趋势上看是CI < NCI)。这一结果与我们的研究假设是一致的,证明了识别成分及计算成分的存在。这是因为:在解决计数条件的问题时,被试主要采用识别成分,且识别成分的存在有利于解题(注视时间短、注视次数少,回视次数少);在解决非计数条件的问题时,主要采用计算成分,计算相邻元素的间隔,所以加工过程更为复杂(注视时间长、注视次数多、回视次数多)。
然而,关于识别成分,仍有一些问题需要进一步澄清。例如NCT或NCI任务中是否也存在识别过程(即首先进行识别;当识别成分无法完成求解时,才调用计算成分),基于本实验的数据无法进行推断。未来可以采用时间分辨率和采样频率更高的眼动设备,或者结合功能磁共振激活检测技术进一步研究这一问题。
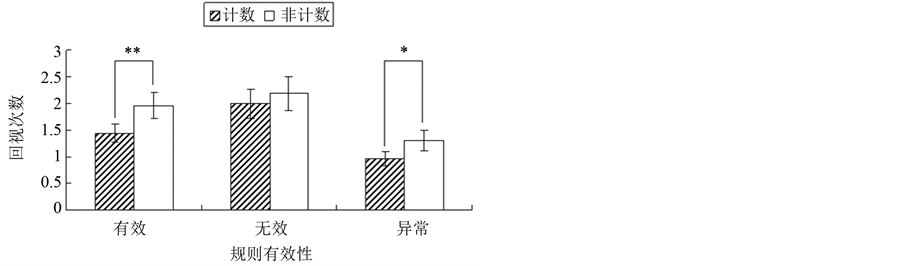
Figure 3. The number of regression
图中**表示p < .005,*表示p < .05。
图3. 回视次数
4.2. 检查成分
按照注视时间和注视次数,无效任务均长或多于有效任务;特别地,根据回视次数,无效任务显著或接近显著地多于有效任务(CI > CT,NCI > NCT)。这一结果说明了在解决正确条件的问题和无效条件的问题时,存在不同的加工过程,进而说明了检查成分的存在;在解决无效条件的问题时,在遇到“错误”数字造成无法用简单规则描述序列时,被试常会进行“回视”再加工,以便确认是否是由于编码或计算错误造成的,因而使得加工过程更为复杂,表现为注视时间长、注视次数多、回视次数多。
也有一些文献研究个体的主观体验对判断任务的影响,例如,Higgins(2000)提出的调节性匹配理论。所谓调节性匹配,指的是个体的自我调节定向与其行为策略之间的匹配。有研究发现,当研究者提示被试尽可能保证判断准确时,经历调节性不匹配体验到错误感(Feeling Of Wrongness, FOW)的被试表现出了更多的纠正行为(张博,2010)。因此,本研究中被试对于无效任务表现出的纠正行为(回视)是否与其主观体验有关(在本研究中,指导语要求被试尽可能快并准确的判断),还需要进行进一步的研究。
5. 结论
本研究首次为数字归纳推理中识别、计算和检查3个子成分的存在提供了眼动证据。本文结果表明,这些子成分是一些相互独立的过程,在不同类型的数字归纳推理任务中被启动和调用。
致 谢
在论文定稿之际,心中颇多感慨。论文的写作过程是艰苦的,但我有幸得到了各位师、领导、同学、朋友、同事和亲人的教诲和帮助。没有他们,也就没有论文的最终成果。
首先我要特别感谢本论文的其它作者三位作者。本文是在他们的悉心指导下完成的。从本文的选题、构思、写作、修改直到最后定稿,都凝聚着他们的智慧、才华与心血。这三位老师学识渊博、治学严谨求实、看待问题高屋建瓴、对待工作非常负责,为人随和坦诚,他们的言传身教将使我终生受益。师恩难忘,在此,向这三位老师表达我最诚挚的敬意与谢意!我还要感谢我的同窗同学,他们在论文写作过程中给予了我很多的帮助。最后我还要感谢我的家人,感谢他们给予我生活和精神上的关心、支持和鼓励,才能毫无后顾之忧的学习。
值此论文完成之际,我谨向以上曾经给予我指导和关心的老师、同学、同事和家人意最诚挚的谢意!
基金项目
本文得到国家自然科学基金(No. 61105118),北京市科技新星项目(No. Z12111000250000),及认知神经科学与学习国家重点实验室开放课题重点项目(No. CNLZD1302)支持。

NOTES
*通讯作者。