1. 引言
系统建模与仿真是研究复杂系统的一种重要方法与手段[1] 。锅炉在工业领域中是一种重要的能量转换装置。它的工作特性直接关系到整个机组的运行状态。同时它又是一类复杂多变量非线性系统[2] ,因此建立一个结构简单同时又具有较高精度的模型是研究锅炉特性的一项重要任务。许多学者基于不同研究目的建立了大量的模型[3] -[7] 。这些模型可以归结为以下几类:静稳态模型、黑箱模型、机理分析模型。静稳态模型一般用于系统稳态设计,但不能模拟系统动态特性;采用系统辨识方法获得的黑箱模型在某些特定的工况下具有较高的精度,然而在其他工况下误差较大,不适合过程控制与优化;机理模型精度较高并且适用范围广,但模型结构往往比较复杂,通常由大量的代数方程和微分方程组成,为了求解这样的代数微分方程组,需要进行大量的简化和变形,这个过程不仅繁琐而且容易出错。此外模型往往包含一些不能通过直接测量而得到参数需要进行标定。本文将多领域统一建模语言Modelica应用到锅炉汽水系统建模中,方程的简化与变形由软件自动完成,减少了出错概率,同时采用Modelica模型标定工具对模型中难于测量的参数进行标定,提高了模型可信度。
2. 多领域统一建模语言——Modelica
Modelica是一种为了解决复杂物理系统多领域统一建模与仿真而产生的一种面相对象、基于组件的非因果关系建模语言。多领域统一建模思想最早由H Elmqvist于1978年提出,随后出现ASCECD、Gproms、NMF、U.L.M.等多种建模语言,为了结束多种物理建模语言并存的混乱局面,1996年9月,国际仿真界开始致力于多领域物理系统混合建模统一语言的研究,这种统一的物理建模语言被称为Modelica[8] 。
Modelica采用面向对象思想进行建模,通过封装和继承机制提高代码的可重用性,同时结合模块化建模可以一个将复杂系统分解为简单的子系统,分别对子系统进行建模,然后采用分层机制、组件连接机制构建系统模型,从而降低了复杂系统建模难度。由于采用非因果的建模思想,用更加自然的语法和语义来表述模型,适合于物理系统的建模,正在向复杂物理系统建模与仿真的标准语言发展[9] 。
3. 锅炉汽水系统模型
3.1. 对象描述
典型的自然循环锅炉结构简图如图1所示。给水在上升管处受热蒸发,导致下降管和上升管存在密度差,形成一定自然循环压头,迫使给水按照下降管–上升管–下降管方式循环流动。上升管出口为汽
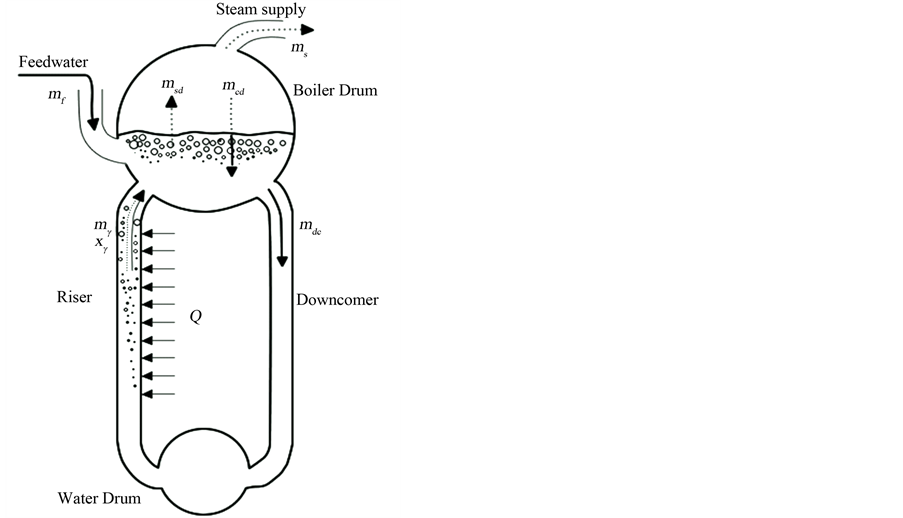
Figure 1. Schematic diagram: Boiler Water-Steam System
图1. 锅炉汽水系统结构简图
水混合物,在汽包内的汽水分离器作用下,蒸汽被送往做功单位,水与汽包水部的水混合继续循环流动。为了保证汽包水位在一定的范围,还需要不断补充给水。
3.2. 二阶Modelica模型
在建模中令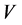 表示容积,
表示容积,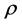 表示密度,
表示密度,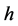 表示比焓,
表示比焓,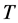 表示温度,
表示温度,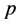 为压力,
为压力,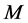 为质量,
为质量,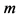 为质量流量。另外下标
为质量流量。另外下标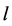 ,
,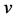 ,
,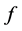 ,
,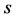 ,
,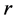 和
和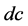 分别代表水、蒸汽、给水、供汽、上升管和下降管。对于整个锅炉,根据质量守恒和能量守恒有:
分别代表水、蒸汽、给水、供汽、上升管和下降管。对于整个锅炉,根据质量守恒和能量守恒有:
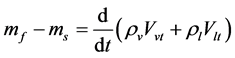 (1)
(1)
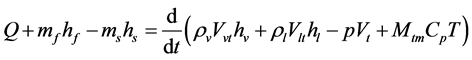 (2)
(2)
其中: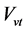 为锅炉蒸汽容积,
为锅炉蒸汽容积,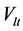 为锅炉水的容积,
为锅炉水的容积,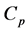 为金属比热,
为金属比热,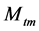 为金属质量,
为金属质量,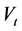 为锅炉总容积,并有如下关系式:
为锅炉总容积,并有如下关系式:
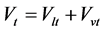 (3)
(3)
由于模型中包含两个状态变量,该模型又称为二阶模型。二阶模型能够真实的模拟给水扰动、燃料扰动、负荷扰动下的压力动态特性。但不能模拟汽包水位动态特性。由于建模时是从锅炉整体列写质量守恒和能量守恒方程,因此具有通用性。从面向对象建模观点看,二阶模型属于锅炉模型的一个基类,更复杂的模型可以通过继承基类的基础上不断细化。二阶模型Modelica表达如图2所示。
3.3. 四阶Modelica模型
二阶模型可以模拟锅炉压力的动态特性,但要模拟锅炉水位特性还需要建立更加复杂的模型考虑锅
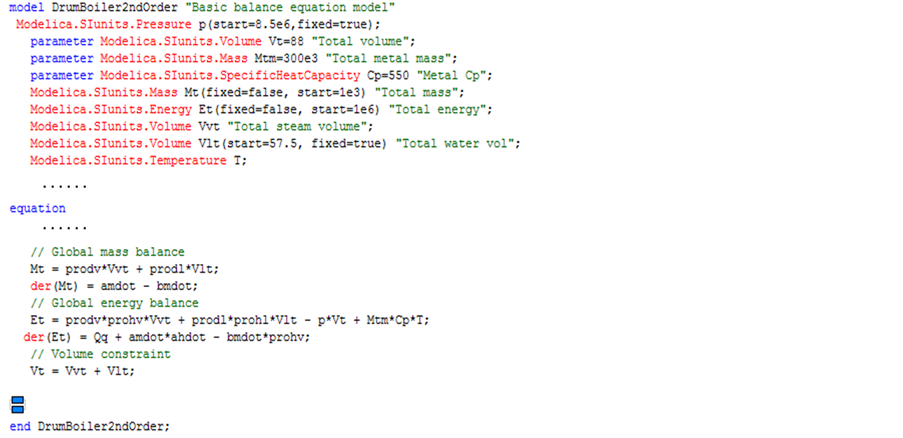
Figure 2. Second-order model of Modelica
图2. 二阶Modelica模型
炉内部汽水分布状态。对汽水分布状态的处理有多种方法。文献[10] 引入漂移流,结合漂移方程推导出了蒸发速度与空泡份额关系。文献[5] 结合均相流模型与上升管稳态条件下质量、能量和动量方程,导出了沿管长方向的特性分布。另一种简便的方法是假设受热管内蒸汽质量分数沿管长方向按线性化分布。在这种假设下上升管内平均汽包份额与上升管出口质量分数有如下关系:
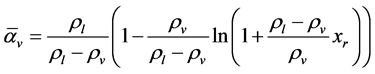 (4)
(4)
由上升管质量守恒和能量守恒方程有:
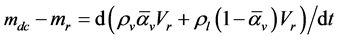 (5)
(5)
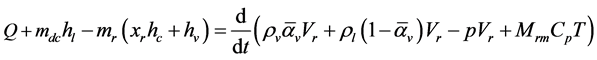 (6)
(6)
其中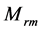 为上升管金属总质量。
为上升管金属总质量。
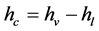 (7)
(7)
根据汽包液面下蒸汽质量守恒有:
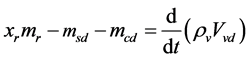 (8)
(8)
式中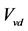 表示汽包水部蒸汽容积,
表示汽包水部蒸汽容积,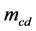 为凝结量,并按下式计算:
为凝结量,并按下式计算:
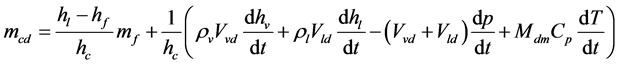 (9)
(9)
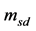 为穿越液面的蒸汽流量,由经验公式计算:
为穿越液面的蒸汽流量,由经验公式计算:
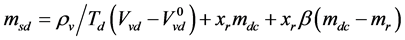 (10)
(10)
其中,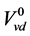 表示没有冷凝时汽包蒸汽容积,
表示没有冷凝时汽包蒸汽容积,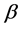 为经验系数,
为经验系数, 为时间常数:
为时间常数:
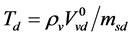 (11)
(11)
根据一维动量守恒,汽水循环流量由下式计算:
 (12)
(12)
四阶Modelica模型如图3所示。通过Modelica语言的extends关键字继承了二阶模型所有代码。此外,模型中使用到的水和水蒸汽热力性质函数由Modelica标准库中提供。
3.4. 水和水蒸汽热力性质计算
从模型的建立过程中可以看出,由于Modelica具有基于方程无因果建模特性,因此代数微分方程可以保持原有的基本结构,方程组的变形和约简由平台软件自动完成,可以避免繁琐的过程,减少出错概率。
此外要完成模型的求解还必须进行水和水蒸汽热力性质计算。Modelica提供了一套计算精度高、运行速度快的标准工质库Modelica.Media.water,该库基于IF97公式(The IAPWS Industry Formulation 1997 for the Thermodynamic Properties of Water and Steam)提供了求解水和水蒸汽热力性质函数库[11] [12] 。
Modelica中定义一个包含饱和状态下温度、密度、比焓等热力性质参数的记录集,如图4所示。在使用记录集前需要建立计算热力性质记录集函数,如图5所示。在模型中使用记录集,首先需定义饱和状态下水和蒸汽热力性质记录集变量,然后利用记录集计算函数进行求解,记录集数据通过点运算获取。
4. 模型标定
锅炉汽水系统模型包含的参数中一些涉及面积、体积和质量等结构参数,可以通过设计资料获取或是通过物理实验测量获得,然而还有一些参数如摩擦系数k、无冷凝时液位下汽泡体积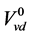 、汽泡在汽包停留时间
、汽泡在汽包停留时间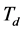 等参数不能直接获得,如果通过多次物理实验的方式来确定,不仅效率低下,而且得到的结
等参数不能直接获得,如果通过多次物理实验的方式来确定,不仅效率低下,而且得到的结

Figure 3. Fourth-order model of Modelica
图3. 四阶Modelica模型

Figure 4. The record of saturated parameter
图4. 饱和参数记录集
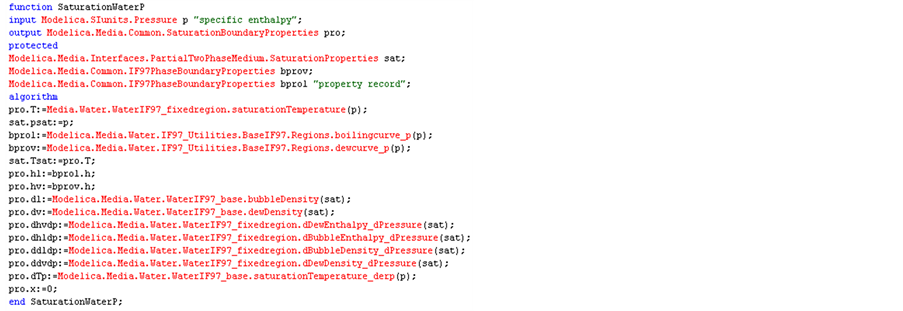
Figure 5. Function of saturated properites
图5. 饱和性质计算函数
果也不够精确。通过仿真模型进行参数标定(也称参数估计)可以快速准确的确定模型参数。在数学上,参数调节过程实际为一种优化过程,旨在最小化仿真结果与测量数据之间的误差。模型标定就是以实验得到的测量数据为依据,在某一范围内自动调整参数值并同时进行仿真,通过比对模型仿真数据与实验测量数据的差异,使得模型输出与测量结果达到最大程度的吻合。
4.1. 参数扰动
前面利用Modelica语言建立了结构相对简单锅炉汽水系统锅炉模型,但仍然有摩擦系数k、无冷凝时液位下汽泡体积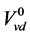 、金属质量
、金属质量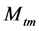 等参数需要进行标定。
等参数需要进行标定。
进行标定前先通过参数扰动来分析各参数对模型的响应关系,参数扰动下水位和压力响应分别如图6、图7。从图可以看出金属质量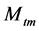 对压力动态特性影响具有主导作用,而对水位动态特性影响作用很小。摩擦系数k、无冷凝时液位下汽泡体积
对压力动态特性影响具有主导作用,而对水位动态特性影响作用很小。摩擦系数k、无冷凝时液位下汽泡体积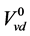 对压力动态特性几乎不起作用,但对水位动态特性影响很大。
对压力动态特性几乎不起作用,但对水位动态特性影响很大。
4.2. 参数标定
参数扰动仿真实验表明:金属质量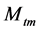 可以通过压力响应曲线来标定,而摩擦系数k、无冷凝时液位下汽泡体积
可以通过压力响应曲线来标定,而摩擦系数k、无冷凝时液位下汽泡体积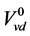 可以通过水位响应曲线进行标定。
可以通过水位响应曲线进行标定。
选取模型中金属质量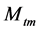 为被调参数并设定约束条件,以50%负荷热量增加10 MW时压力阶跃响应曲线为依据,通过计算模型仿真结果变量
为被调参数并设定约束条件,以50%负荷热量增加10 MW时压力阶跃响应曲线为依据,通过计算模型仿真结果变量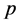 与对应的测量变量在各个测量时间点上的残差平方和为准侧,
与对应的测量变量在各个测量时间点上的残差平方和为准侧,
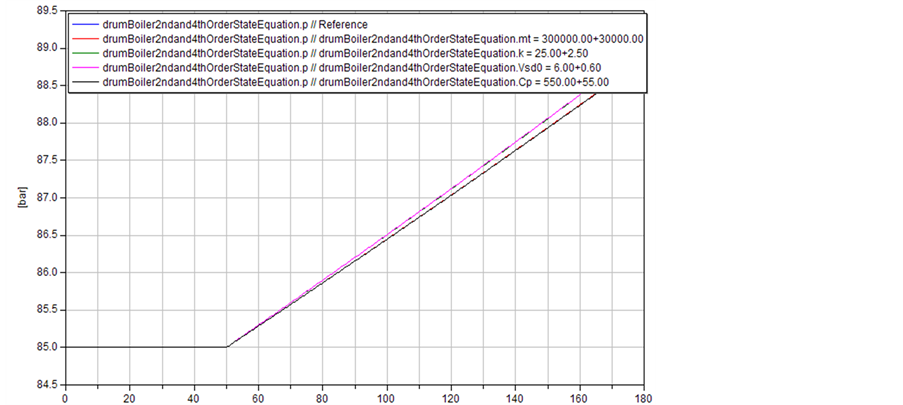
Figure 6. Curve: Pressure of disturbed experiment
图6. 参数扰动对压力影响
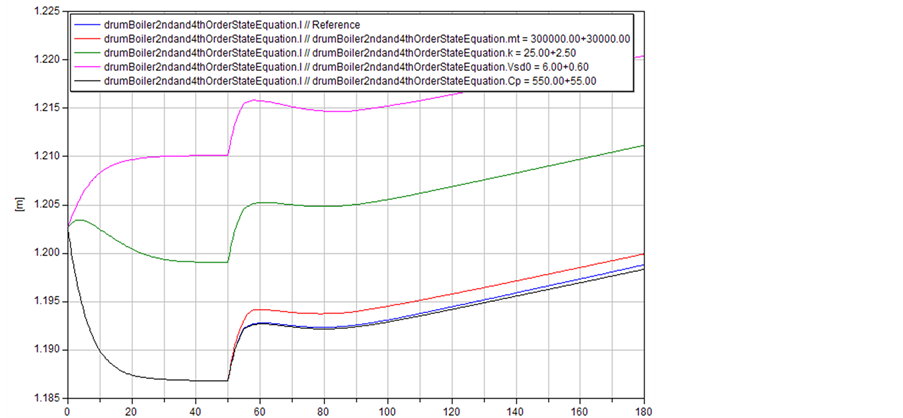
Figure 7. Curve: Temperature of disturbed experiment
图7. 参数扰动对水位影响
将该值的最小化作为标定目标对参数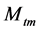 进行标定。标定前后及实验值对比如图8所示。标定后残差的平方和由初始的20061.5减少为100.389。
进行标定。标定前后及实验值对比如图8所示。标定后残差的平方和由初始的20061.5减少为100.389。
选取模型中摩擦系数k、无冷凝时液位下汽泡体积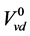 为被调参数并设定约束条件,以50%负荷热量增加10 MW时水位阶跃响应曲线为依据,通过计算模型仿真结果变量
为被调参数并设定约束条件,以50%负荷热量增加10 MW时水位阶跃响应曲线为依据,通过计算模型仿真结果变量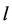 与对应的测量变量在各个测量时间点上的残差平方和为准侧,将该值的最小化作为标定目标对参数k和
与对应的测量变量在各个测量时间点上的残差平方和为准侧,将该值的最小化作为标定目标对参数k和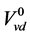 进行标定。标定前后及实验值对比如图9所示。标定后残差平方和由初始的0.0108846减小为0.00246737。
进行标定。标定前后及实验值对比如图9所示。标定后残差平方和由初始的0.0108846减小为0.00246737。
4.3. 模型验证
为了验证模型的有效性,将50%负荷耗汽量增加10 kg/s阶跃变化时,模型标定前后压力和水位响应特性曲线与测量值进行对比,如图10所示。图中蓝色曲线为压力和水位测量值,红色曲线为模型标定后
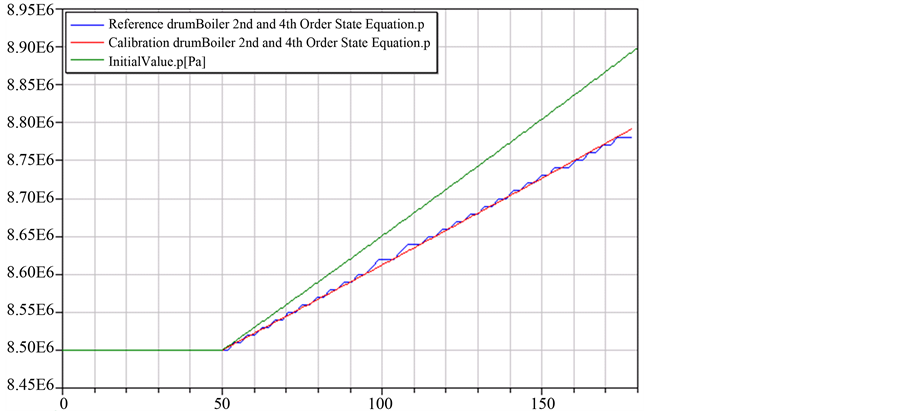
Figure 8. Curve: pressure of simulation results and measured
图8. 模型标定前后与实测压力动态特性曲线
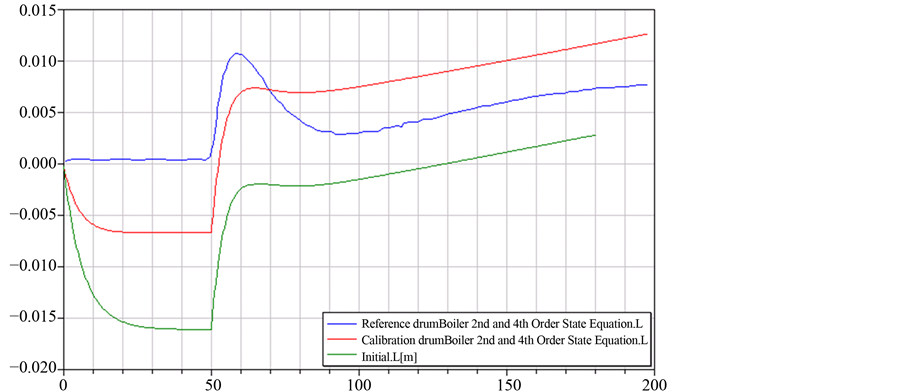
Figure 9. Curve: drum level of simulation results and measured
图9. 模型标定前后与实测汽包水位动态特性曲线
压力和水位特性曲线,绿色曲线为模型标定前压力和水位特性曲线。从图10可以看出,通过对模型进行标定,压力动态特性几乎与测量值完全一致,水位动态特性尽管与测量值还存在一定偏差,但也得到了进一步改善。这也说明在锅炉汽水系统中水位动态特性要比压力动态特性复杂。此外,仿真结果说明以燃油阶跃响应特性为依据进行标定的锅炉汽水系统模型,在耗汽量阶跃扰动下仍然得到了优化,表明通过标定可以获得全局最优模型。
5. 结论
将多领域统一建模语言Modelica引入到锅炉汽水系统建模中,在Bell模型的基础上建立了二阶和四阶Modelica模型,并在Dymola平台上进行仿真。二阶Modelica模型从锅炉整体能量和质量守恒推导得出,反映了锅炉系统最基本动态特性,是锅炉模型的基类。四阶Modelica模型通过继承二阶模型并考虑汽包和上升管处汽水分布特性而获得,它更详细的反映了锅炉内部动态特性。Modelica作为一种面向对
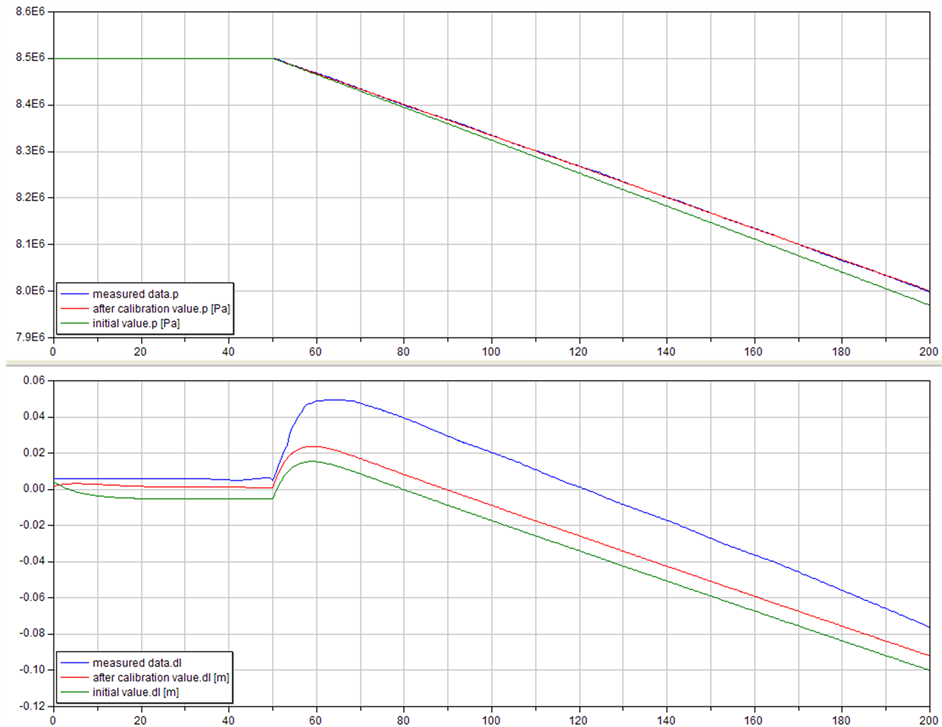
Figure 10. Comparison of model and measured data for perturbations in steam flow rate
图10. 耗汽量阶跃变化时模型标定前后压力和水位动态特性曲线与实测值对比
象的无因果关系建模语言,它可以自动将DAE方程转换为ODE方程进行求解,避免了对方程组进行手动变形和约简等繁琐的过程,提高建模效率。同时Modelica采用IF97标准提供了一套完整的高精度的工质热力性质库,解决了水和水蒸汽热力性质求解问题。为了确定模型中难于测量的参数,采用多目标优化方法对锅炉模型中的参数进行标定,通过标定提高了模型的可信度。