1. 引言
在天体物理、惯性约束聚变(ICF)和高能量密度物理以及激光等离子体软X射线激光物理等许多研究领域中,高剥离态离子的辐射和碰撞过程一直处于非常重要的地位。近年来,随着激光技术的迅猛发展和惯性约束热核聚变研究的迫切需要,高离化态重离子发射光谱已成为人们关心的中心课题之一。类镁光谱在近几年中得到了很广泛的研究,特别是随着各种先进的离子源、高功率激光器、托卡马克等实验技术的发展,高Z元素高剥离态的研究越来越引起人们的关注。对高剥离元素的跃迁波长、跃迁能量和振子强度等原子跃迁参数的准确计算就显得尤其重要,进而类镁离子的高剥离态离子成为等离子体系中研究的重要对象[1] 。
早期类镁电子的研究内容主要包括实验和理论的能级、振子强度,跃迁几率和能级寿命。早期关于类镁等电子序列的研究主要有两个局限,一是缺乏部分离子的相关数据;二是部分数据以图片形式出现,不够准确,或者计算精度不够;本文所研究的对象也存在上述两个问题。
本文正是这样的基础上,利用多组态Dirac-Fock方法,通过考虑电子关联效应,去获得更加精确的数据和理解差距产生的原因。所谓关联效应最初定义为能级的实验值和考虑了相对论效应修正后的DiracFock解的差。而电子关联效应,就是指价电子与原子实内的电子之间的相互作用。国外已经有大量的文献报道,我们小组也做了相应的工作[2] -[4] 。研究表明电子关联效应对于原子的能级结构和跃迁特性有很大的影响,考虑了电子关联效应后能够获得更加精确的数据。本文主要研究了研究类Mg离子的特性。这些离子闭壳层外有两个价电子,是典型电子关联效应研究的对象。和先前工作一样,我们选取基于多组态Dirac-Fock方法的GRASPVU程序包来进行计算。
2. 方法
2.1. 理论
本文所用的多组态Dirac-Fock理论(MCDF)方法在文献[5] 中已有详细描述,这里仅作扼要的介绍。在多组态Dirac-Fock理论中,一个核电荷数为Z、具有N个电子的原子或离子体系的Dirac-Coulomb哈密顿量为(原子单位)。
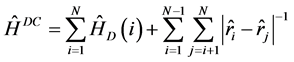 (1)
(1)
这里的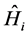 是第i个电子的Dirac哈密顿量,可表示为
是第i个电子的Dirac哈密顿量,可表示为
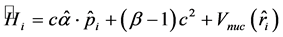 (2)
(2)
其中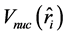 是核势场,
是核势场,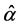 和
和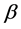 分别是Dirac矢量和标量矩阵,
分别是Dirac矢量和标量矩阵,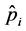 是第i个电子的动量算符,c是真空中光速。
是第i个电子的动量算符,c是真空中光速。
在中心场近似下单电子的旋轨波函数可表示为
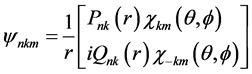 (3)
(3)
式中k为Dirac量子数,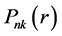 和
和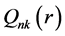 分别为相对论径向波函数的大小分量,
分别为相对论径向波函数的大小分量,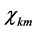 为自旋函数。
为自旋函数。
N电子体系的组态波函数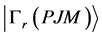 是所有单电子旋–轨波函数组成的N阶Slater行列式波函数
是所有单电子旋–轨波函数组成的N阶Slater行列式波函数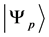 的线性组合,即
的线性组合,即
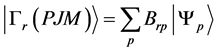 (4)
(4)
在MCDF方法中,任一原子态α的波函数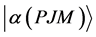 由具有相同P,J和M量子数的组态波函数,
由具有相同P,J和M量子数的组态波函数,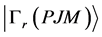 线性组合而成,即
线性组合而成,即
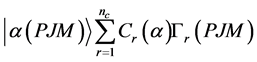 (5)
(5)
式中nc是组态波函数的个数,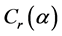 为组态混合系数。
为组态混合系数。
对角化由原子波函数(5)式构造的哈密顿矩阵,则可得到相关原子态的能量和组态混合系数。对于其他高阶效应,如Breit修正和主要的量子电动力学QED效应,可作为微扰处理。
2.2. 过程
本小节主要介绍我们所用的计算方法。简单而言主要是通过逐次增加基矢数目来尽可能多的考虑组态相互作用,直至得到收敛的结果。应用的具体计算方法如下:
1) 采用限制电子活动空间的方法(Restrictive active space methods)产生组态状态波函数(Configuration state function)列表。本工作采用的限制电子活动空间方法是指电子被限制在某些特定的活动轨道之间进行跃迁。自洽场迭代收敛能量最小值往往与主量子数相同的组态能量较为接近,因此逐次增大主量子数n,产生组态状态波函数基组列表。同时在计算中引入轨道层(orbital layer)的概念,将主量子数(l),相同而轨道角动量(m),量子数(n)不同的组态划分为同一个轨道层。例如:把{1s,2s,2p}的轨道基组叫做n = 2轨道层, 把{1s,2s,2p,3s,3p,3d}的轨道基组叫做n = 3轨道层,依次类推。但是考虑到计算量和计算时间,组态状态波函数基组不易过大,且有些电子不真实存在某些轨道上,因此在计算当中有必要适当的限制电子活动轨道。对于不同的模型,主量数(n)的限制要作相应的调整。由于类Mg离子最外层有两个电子,因此要考虑双激发对跃迁参数的贡献,同时为了最大限度接近实验值,在本文的计算当中我们都考虑了双激发。
2) 在组态状态波函数基组生成以后,需要对多电子Dirac-Coulomb哈密顿量矩阵元进行角积分。在这一步里,初始波函数是由Thomas-Fermi模型势给出的。同时在初次进行自洽场计算的时候,需要对所有的轨道都进行优化。当逐次增加主量子数n的时候,对轨道的优化也是一层一层进行的。在这个方案下,首先我们优化n轨道同时保持n − 1轨道不变。然后我们分别优化n + 1轨道同时保持前面已经优化的轨道不变。同时,我们注意到在计算当中涉及了多条能级,因此采用文献[6] 给出的开展能级优化计算EOL模型(Extended Optimal Level calculation),对应于同一LS谱项的精细结构能级的平均的优化权重为(2J + 1),
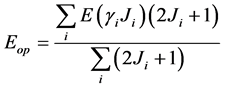 (6)
(6)
同时,我们在计算中,将自洽场收敛的标准设为10−8。
3) 得到基组的径向波函数以后,加入第二章提到的Breit修正、量子电动力学修正已得到对角化包括Breit修正项、真空极化和自能修正项的哈密顿量得到组态状态波函数扩展系数。在这个相对论组态相互作用的计算过程中,程序运用了文献[6] 中的迭代Davidson方法和稀疏矩阵表示方法。
4) 在获得跃迁波长、阵子强度、线强度和跃迁几率之前,我们要将组态混合系数由块模式转化为非块模式,使得初态和末态组态基组变得正交,得出想要的结果。
3. 结果与讨论
3.1. 能级
为了更好的说明问题,当前的计算结果分成两部分,一部分是考虑电子关联效应中的Valence-Valence (VV)效应,一部分是考虑电子关联效应中的Core-Valence (CV)效应。表1给出了基于MCDF方法的VV和CV两种模型下类Mg的离子3s3p(3P0,1,2,1P1)的能级,结果包含了量子电动力学效应和特殊质量位移,其中量子电动力学效应考虑了两种修正:自能和真空极化。表1的实验结果是来自于NIST[7] 。需要说明的是,NIST并没有给出Br类Mg的1P1能级,因此我们用Zeng等人的结果[8] 来代替。考虑电子关联效应后,导致组态波函数急剧增加,这对于计算的收敛性和程序本身的计算能力、计算时间要求相对提高很多,因此在保证计算精度的条件下,有必要对扩展的主量子数进行限制。正如表1列出的,对于VV模型,主量子数限定在n ≤ 7,其对应的最大波函数数目为698;CV模型n ≤ 6,其波函数数为13,069。尽管对主量子数进行了限制,计算的结果仍然可信,这是因为本文的结果正是建立在增加波函数基矢数目的基础上来考虑电子关联效应的。
从表1可以看出,考虑电子关联效应,CV的结果要更加接近与实验值。VV的计算值与实验值的偏差在0.006%~0.412%之间,而CV的值而言,若不考虑1P1能级,偏差在0.001%~0.064%之间。CV模型下的1P1能级与实验值的偏差则在0.177%~0.686%之间,但是如果没有考虑电子关联效应,1P1的能级与实验值偏差在0.447%~1.034%之间,因此可认为,考虑电子关联效应后,CV计算的能级与实验符合很好。为了更好说明电子关联效应对1P1能级的影响,我们在图1给出了随扩展主量子数变化的VV、CV与实验值的偏差。
对于两种模型来说,随着主量子数的扩大,两种模型的结果与实验结果更加接近,但是对于VV模型来说,n = 6与n = 7的结果最大偏差不到1 cm−1,也就是说n = 7的轨道对于3s2和3s3p能级的影响相当小,也从一个侧面说明了当前计算对于主量子数的限制是可行的。同时我们可以发现,高n层的旁观电子对于计算的结果有很大的影响,CV模型更为明显,这点在我们先前的文章也有类似的结论[3] [4] 。
同时为了说明当前计算结果是可信的,我们在表2中比较了不同方法的计算出的类Mg的Cu XVIII能级值。其中的CIV3的计算结果是由Tayal[9] 等人理由基于组态相互作用的CIV3程序给出的,MCHF的结果则是由Tachieve等人[10] 给出的。从表2可以看出,当前CV的计算值要优于CIV3 MCHF的计算值。同时我们注意到,对于1P1能级而言,除了CIV3修正后的结果,其它理论结果与实验值偏差都有点大。考虑电子关联效应之后,CV值要优于其它理论计算值。
3.2. 波长
低密度等离子体中发射的自旋禁戒的谱线可以被认为是很好的诊断手段。因此准确的波长对于研究

Table 1. The energies of Mg-like 3s3p levels
表1. 类Mg的离子的3s3p能级(cm−1)
a:文献[8] 。

Figure 1. The electron correlation on 1P1 energy level
图1. 电子关联效应对1P1能级的影响
等离子体的状态是必不可少的。同时为了验证当前计算的可信性,我们在表3给出了Z = 25~42的类Mg离子的理论计算值和实验值。同时在表三也列出了Tachieve等人[9] 的MCHF计算值。表3中的实验值是

Table 2. The experimental and theoretical results of Cu XVIII
表2. Cu XVIII能级(cm−1)的实验值和理论计算值
a:CIV3原始计算值;b:CIV3修正值。

Table 3. The wavelengths of Mg-like ions (Å) (Mn XIV-Mo XXXI)
表3. 类Mg离子的波长(Å) (Mn XIV-Mo XXXI)
由Seely等人[11] ,Sugar等人[12] 以及NIST给出的。从表3可以看出,两种模型和MCHF方法给出的Mn XIV-Mo XXXI离子1S0-3P1跃迁波长都与实验值存在偏差,其中VV偏差在0.71~2.70 Å,CV偏差在0.001~0.229 Å,而MCHF偏高在0.65~2.244 Å;对于Mo XXXI而言,我们注意到1S0-1P1当前计算的CV与实验值的偏差最大为0.229 Å,这要明显好于MCHF和VV的计算值,因此我们认为考虑电子关联效应对于精确的波长有重要的影响。
3.3. 振子强度
对于从i态到j态跃迁的振子强度和跃迁几率的关系可以用下面的公式来定义:
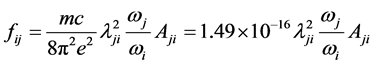 (7)
(7)
其中,m和e分别是电子质量和电荷,c是光速,λji是跃迁波长(Å),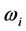 和
和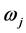 分别是下能级i和上能级j的权重(简并度)。对于电偶极跃迁(E1)来说,跃迁几率和振子强度可以给出如下的形式:
分别是下能级i和上能级j的权重(简并度)。对于电偶极跃迁(E1)来说,跃迁几率和振子强度可以给出如下的形式:
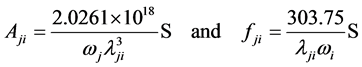 (8)
(8)
其中的S是线强度,单位为原子单位(au),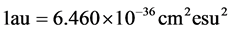 。
。
表4给出了类Mg离子的3s2-3s3p(3P1,1P1)跃迁的振子强度,同时也给出了来自MCHF的结果[10] ,Safronova等人的结果[12] ,以及Huang等人的结果[13] 。可以看出,类Mg离子的振子强度随元素序数的增加而减少。MBPT的计算值要低于其它所有理论的计算值,但是随着元素序数的增加,偏差也在逐渐缩小。VV、CV、MCHF以及Huang的结果大体在一个数量级,彼此之间的偏差不超过10%。Huang等人的结果被证明与NIST给出的结果相差小于1%,因此我们可以比较CV与Huang等人的结果来确保当前计算的可信性。可以看出,CV的计算值与Huang等人的结果数值上很接近,因此我们认为当前的计算是可信而且准确的。同时我们发现VV的计算值不总是差于CV的计算值,对于Cu XVIII的1S0-1P1跃迁的振子强度,VV的计算值为0.733,要比CV的计算值0.761,更接近Huang等人给出的0.741。由
于目前尚无实验值,所以暂时无法解释这一现象。
3.4. 能级寿命
能级j的能级寿命τ可以表示为:
 (9)
(9)
能级寿命作为一个可以被测量的量,可以用来检验理论计算的准确性。因此在表5和表6分别给出

Table 4. The oscillator strengths of 3s2-3s3p(3P1,1P1) transitions of Mg-like ions
表4. 类Mg离子3s2-3s3p(3P1,1P1)跃迁的振子强度

Table 5. The lifetimes of Mg-like ions 3P1 energy level (S−1)
表5. 类Mg离子3P1的能级寿命(S−1)
a:文献[15] 。

Table 6. The lifetime of Mg-like ions 1P1 energy levels (1011 S−1)
表6. 类Mg离子1P1的能级寿命(1011 S−1)
a:文献[7] ;b:文献[16] 。
了3s3p(3P1和1P1)的能级寿命,其中,表格中的拟合值为Curtis在1991年根据当时的实验值和一些理论结果拟合产生的[14] 。对于3P1,VV的计算结果与拟合值偏差在1.89%~12.5%,CV与拟合值的偏差为0.77%~4.94%,MCHF与拟合值的偏差为3.83%~12.6%,而MBPT与拟合值的偏差为4.73%~11.26%。可以看出考虑电子关联效应后,CV的计算值与拟合值更加接近。
对于类Mg离子1P1的能级寿命而言,我们发现理论值与拟合值的符合要比3P1的情况要好,VV的计算结果与拟合值偏差在1.94%~6.34%,CV与拟合值的偏差为0.93%~5.39%,MBPT与拟合值的偏差为9.87%~13.08%。如果不考虑Br XXIV和Mo XXXI,则MCHF与拟合值的偏差为9.45%~12.62%。同时我们注意到表5和表6中NIST给出的实验值与拟合值有0.29%~6.94%的偏差,我们认为有两个原因,一是NIST给出的实验值,其自身的不确定度就在20%;二是当时拟合时,实验数据较少,因而拟合点少造成拟合公式不是很精确。如果考虑这两个因素,我们认为考虑电子关联效应后,CV的值是可信的。但是由于类Mg的实验大多是在上世纪80年代完成的,受制于当时条件,造成实验精度不是很高,因此能级寿命的测量需要更加精确的实验来完成。
4. 结论
本文运用多组态Dirac-Fock方法,考虑电子关联效应,详细计算了类Mg离子的能级,波长,振子强度和能级寿命,结果表明考虑电子关联效应后,当前CV的结果与已有的实验结果及理论结果符合很好。这些结果对于理解类Mg离子的不同效应有重要的意义,同时对于分析已有的实验结果和指导未来的实验也有重要的意义。
项目基金
国家自然科学基金(11304266, 11105129)的资助。