1. 引言
随着我国水电开发的推进,西南地区已形成多个规模巨大的梯级水库群,这些梯级水库群具有级数多,装机大,输送电范围广等特点,合理的运行管理方式才能充分发挥这些梯级水库群的兴利除害作用,发挥其经济和社会效益[1] [2] 。梯级水库群调度规则是指导水库日常运行管理的有效工具,随着我国水电规模不断扩大,如何制定梯级水库群调度规则成为水利发展迫切需要解决的问题。调度函数是水库调度规则的一种重要形式,常采用隐随机优化方法制定,即:根据历史来水资料,从长系列的确定性优化调度样本中获取决策规律[3] 。制定调度函数常用的方法包括线性回归分析、神经网络、遗传算法等[4] -[7] 。
调度函数一般采用库容、可用水量等作为状态变量[8] [9] ,对实际调度中结合中长期预报的梯级调度函数研究较少。造成理想来水信息情况下的优化调度效益在实际应用中无法完全实现。针对以上问题,本文提出基于可用水量预测的调度函数及其优化模型。该模型中的调度函数以当前时段采用季节性ARIMA模型[10] 预报来水量叠加有效库容的可用水量预测值替代常用的可用水量作为状态变量构建调度函数,通过对长系列确定性优化调度结果中出力决策与可用水量预测值的多元线性回归分析得到初始调度函数。在此基础上,以模拟多年平均发电量最大为目标,以梯级保证率和保证出力破坏程度为约束条件,建立调度函数优化模型,采用坐标轮换的逐步搜索方法求解。澜沧江中下游梯级水库群的实例研究表明,新的调度函数在制定阶段就已充分考虑到了径流预报及其不确定性的影响,应用中更易于与长期径流预报模型结合,切合实际调度情况,模拟效果各项效益指标也优于以可用水量为状态变量的调度函数。
2. 调度函数原理与方法
调度函数是根据确定来水长系列最优化调度过程,合理选取决策变量、状态变量及函数形式,通过统计分析等方法提取得到的某种函数形式的调度规则。一般可用以下形式表示:
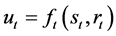 (1)
(1)
式中: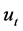 表示
表示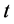 时段水库调度决策值(出力或下泄流量等);
时段水库调度决策值(出力或下泄流量等);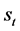 为
为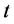 时段初水库状态(水位或蓄水量等);
时段初水库状态(水位或蓄水量等);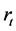 为
为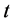 时段水库预报来水。一般来说这种函数关系应该是非线性的,但非线性函数难于处理,且种类较多,不易确定具体类型,而线性函数直观、简便,因此较多研究采用线性处理来表达这种函数关系,即:
时段水库预报来水。一般来说这种函数关系应该是非线性的,但非线性函数难于处理,且种类较多,不易确定具体类型,而线性函数直观、简便,因此较多研究采用线性处理来表达这种函数关系,即:
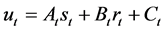 (2)
(2)
式中: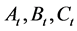 为
为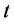 时段调度函数各项系数。
时段调度函数各项系数。
当调度函数形式选择线性时,可通过多元线性回归分析方法求得各项系数及函数具体表达式。多元线性回归原理如下:
如果因变量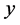 与
与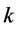 个自变量
个自变量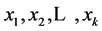 之间存在线性关系,则:
之间存在线性关系,则:
 (3)
(3)
式中: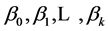 为回归系数,是
为回归系数,是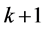 个待估计参数;
个待估计参数;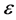 为随机误差。
为随机误差。
设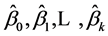 分别是参数
分别是参数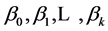 的最小二乘估计,则多元线性的回归方程为:
的最小二乘估计,则多元线性的回归方程为:
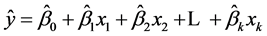 (4)
(4)
根据最小二乘法,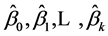 应使得全部观测值与回归值的偏差平方和达到最小,即:
应使得全部观测值与回归值的偏差平方和达到最小,即:
 (5)
(5)
当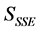 对
对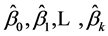 的各个偏导数等于0时,
的各个偏导数等于0时,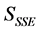 达到最小,求解偏导方程组便可求得参数估计值
达到最小,求解偏导方程组便可求得参数估计值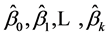 ,进而得到回归方程。
,进而得到回归方程。
多元线性回归得到的调度函数是基于优化调度样本拟合的,而拟合必然存在着一定的误差,且不能考虑全调度时段整体效益。为了检验调度函数的性能并对调度函数进行优化,往往需要对调度函数进行模拟调度,根据模拟调度结果对调度函数的各项系数进行修正,优化调度函数。以往研究在模拟调度及优化调度函数时多采用历史径流资料,以可用水量为状态变量得到调度决策值,而没有考虑结合来水预报时预报误差对调度函数应用效果的影响。针对以上问题,本文提出以可用水量预测值为状态变量的调度函数及其优化模型。
3. 基于可用水量预测值状态的调度函数
对于以发电为主的梯级水库群,选择梯级各水库面临时段出力作为决策变量,影响决策变量的因素主要为时段初梯级各水库蓄水状态及面临时段各水库预报来水。水库可用水量是常用的调度函数自变量,采用可用水量的梯级水库线性调度函数形式如式(6)所示。
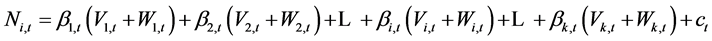 (6)
(6)
式中: 为水库
为水库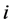 在时段
在时段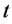 的出力;
的出力;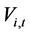 为水库
为水库 在
在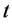 时段初的有效库容;
时段初的有效库容;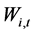 为水库
为水库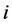 在时段
在时段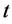 的来水量;
的来水量; 为梯级调节水库个数;
为梯级调节水库个数;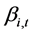 为调度函数
为调度函数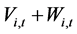 项的系数;
项的系数;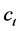 为常数项。调度函数参数可通过多元线性回归得到初值,并采用模拟优化方法修正。
为常数项。调度函数参数可通过多元线性回归得到初值,并采用模拟优化方法修正。
由于以月为时段的调度中,来水量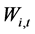 一般难于准确预测,导致决策偏差。虽然在月内可根据水库和来水情况动态对决策进行修正,但调度函数对中长期调度的指导作用将被削弱。为此,本文采用可用水量预测值作为调度函数状态变量,将月来水预报模型与调度函数结合,使得调度函数本身具有适应来水预报偏差的特性,调度函数形式如式(7)所示。
一般难于准确预测,导致决策偏差。虽然在月内可根据水库和来水情况动态对决策进行修正,但调度函数对中长期调度的指导作用将被削弱。为此,本文采用可用水量预测值作为调度函数状态变量,将月来水预报模型与调度函数结合,使得调度函数本身具有适应来水预报偏差的特性,调度函数形式如式(7)所示。
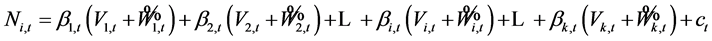 (7)
(7)
式中: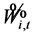 为水库
为水库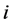 在时段
在时段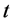 的预测来水量。
的预测来水量。
在估算可用水量预测值时需要面临时段各水库预测来水,来水预报模型的特性将影响调度函数参数取值。本文采用季节性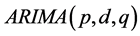 模型对水库入库流量进行预报,其基本思想是通过差分或其他适当方法将非平稳序列转化为平稳序列,然后再以自回归滑动平均(ARMA)模型进行预报。
模型对水库入库流量进行预报,其基本思想是通过差分或其他适当方法将非平稳序列转化为平稳序列,然后再以自回归滑动平均(ARMA)模型进行预报。
4. 调度函数优化算法
初始调度函数采用长系列确定性优化调度结果,通过多元线性回归得到。确定性模型以发电量最大为目标,以保证出力为出力下限约束,以逐步优化算法求解。多元线性回归分析得到的初始调度函数存在着一定的误差,需要通过模拟调度进行检验,若模拟调度不能达到出力及保证率要求的预期效果,可对调度函数的各项系数进行修正,优化调度函数,以满足调度需求。
4.1. 调度函数优化模型
考虑水量平衡等约束条件,确定各电站调度函数系数,使得在兼顾梯级保证率及保证出力破坏程度情况下模拟调度梯级多年平均发电量最大。
1) 目标函数:
发电为主梯级水库群,优化目标取模拟调度梯级多年平均发电量最大:
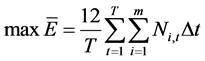 (8)
(8)
式中: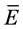 为梯级水库群多年平均发电量(亿kW×h);
为梯级水库群多年平均发电量(亿kW×h);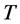 为调度期内时段数;m为电站数目;
为调度期内时段数;m为电站数目;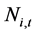 为电站
为电站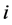 在时段
在时段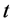 的出力;
的出力;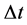 为计算时段长度。
为计算时段长度。
2) 约束条件:
①水量平衡:
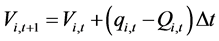 (9)
(9)
式中: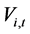 、
、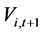 分别为水电站
分别为水电站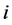 在
在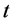 时段初、末的蓄水量;
时段初、末的蓄水量;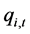 、
、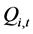 分别为水电站
分别为水电站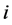 在
在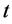 时段入库流量、下泄流量。
时段入库流量、下泄流量。
②水位约束:
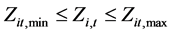 (10)
(10)
式中: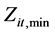 为水电站
为水电站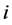 第
第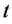 时段允许消落的最低水位,一般为死水位或综合利用要求的最低水位;
时段允许消落的最低水位,一般为死水位或综合利用要求的最低水位;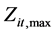 为水电站
为水电站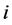 第
第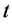 时段的水位上限,非汛期取正常高水位,汛期取汛限水位。
时段的水位上限,非汛期取正常高水位,汛期取汛限水位。
③下泄流量约束:
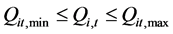 (11)
(11)
式中: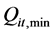 为水电站
为水电站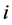 第
第 时段应保证的最小下泄流量;
时段应保证的最小下泄流量;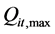 为水电站
为水电站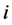 第
第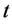 时段最大允许下泄流量。
时段最大允许下泄流量。
④出力约束:
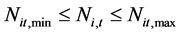 (12)
(12)
式中: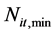 为水电站
为水电站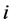 第
第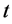 时段应保证的最小出力;
时段应保证的最小出力;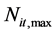 为水电站
为水电站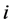 第
第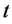 时段允许的最大出力。
时段允许的最大出力。
⑤始末状态:
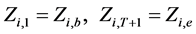 (13)
(13)
式中: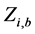 为水电站
为水电站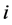 调度期初水库蓄水位,
调度期初水库蓄水位,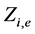 为水电站
为水电站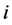 调度期末水库蓄水位。
调度期末水库蓄水位。
⑥梯级发电保证率约束:
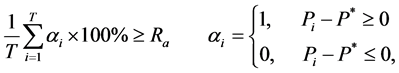 (14)
(14)
式中: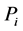 为时段
为时段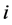 梯级总出力,
梯级总出力,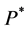 为梯级保证出力;
为梯级保证出力;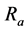 为常数,梯级保证率允许最小值。
为常数,梯级保证率允许最小值。
⑦梯级保证出力破坏程度约束:
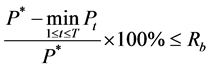 (15)
(15)
式中: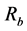 为常数,梯级保证出力破坏程度允许最大值。
为常数,梯级保证出力破坏程度允许最大值。
4.2. 调度函数优化方法
调度函数优化采用坐标轮换的逐步搜索寻优,主要流程如下:
Step 1:设定在梯级多年平均发电量的基础上,兼顾梯级保证率及保证出力破坏程度的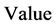 值作为调度函数模拟调度效果评价指标:
值作为调度函数模拟调度效果评价指标:
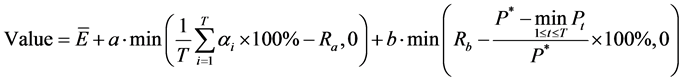 (16)
(16)
式中: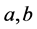 分别为梯级保证率及保证出力破坏程度项惩罚系数,可根据实例研究效果合理确定。
分别为梯级保证率及保证出力破坏程度项惩罚系数,可根据实例研究效果合理确定。
Step 2:将多元线性回归得到调度函数各项系数设为寻优初始解。
Step 3:从第一个调度函数的第一个系数开始逐个优化。固定其它系数,单独调整需要优化的系数。若需要优化的系数为常数项,则在原值基础上分别增大和减小某一常数值,若为非常数项系数,在原值基础上分别增加和降低某一比例。
Step 4:使用调整后的系数组合及原系数组合分别模拟调度,对比三组系数组合的模拟调度对应的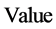 值,选取
值,选取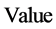 值最大的系数组合作为新的系数解。再调整新的系数解的第二个系数,依次坐标轮换,逐个系数进行寻优。
值最大的系数组合作为新的系数解。再调整新的系数解的第二个系数,依次坐标轮换,逐个系数进行寻优。
Step 5:循环至最后一个系数后再从第一个系数重新循环,直至模拟调度结果满足设定的各项效益指标要求或达到最大循环次数终止。
Step 6:将满足程序设定的各项效益指标的系数解代入调度函数即得到所求优化调度函数。
5. 实例研究
5.1. 基本资料
澜沧江流域是我国十三大水电基地之一,干流中国境内规划按15级开发,总装机容量达到25276.9 MW。本文以澜沧江中下游小湾、漫湾、大朝山、糯扎渡和景洪五座水库组成的梯级水库群优化调度函数制定为计算实例。其中,主要研究小湾、糯扎渡两座控制性水库的调度函数,另外三座水库因库容较小,调节能力相对较差,按照固定各月水位的方式处理。水库群拓扑结构如图1所示。各水库汛期均为6月份至10月份,水库特征属性值见表1。
5.2. 应用结果对比分析
选取澜沧江中下游梯级水库群1953~2010年58年来水资料,以月为计算时段,进行长系列确定性优化调度,获得最优化调度过程,作为制定调度函数的数据样本。确定性优化调度各项效益见表2“确定

Figure 1. Topological structure of cascaded reservoirs
图1. 梯级水库群拓扑结构

Table 1. Characteristic parameters of cascaded reservoirs
表1. 水库特征参数表

Table 2. Results of simulation operation
表2. 模拟调度结果
性优化调度”项。图2为典型丰枯月份7月和11月小湾与糯扎渡出力–可用水量散点图,可见其大致能用一个平面拟合,可以采用线性调度函数。
首先,采用多元线性回归分析方法,选取时段出力为决策变量,两水库可用水量为状态变量,建立以年为调度周期的小湾,糯扎渡各月调度函数。调度函数具体形式如下:
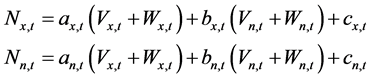 (17)
(17)
式中: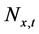 ,
,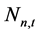 分别为小湾、糯扎渡
分别为小湾、糯扎渡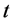 时段平均出力;
时段平均出力;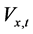 ,
,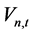 分别为
分别为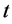 时段初小湾、糯扎渡有效库容;
时段初小湾、糯扎渡有效库容;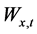 为小湾
为小湾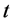 时段来水量;
时段来水量;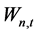 为糯扎渡
为糯扎渡 时段区间来水量;
时段区间来水量;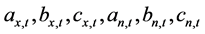 分别为调度函数各项系数。
分别为调度函数各项系数。
而后,采用类似方法以可用水量预测值作为状态变量构建调度函数,并分别以坐标轮换的逐步搜索方法对两种调度函数参数进行优化,在来水预测时采用ARIMA(1,1,1)模型。图3为初始调度函数、可用水量调度函数、可用水量预测值调度函数的模拟调度结果,表2为相应指标统计。结果表明,多元线性回归拟合的初始调度函数梯级年平均发电量尚可,但保证率偏低且梯级保证出力破坏程度较大。根据历史流量资料优化后的调度函数各项指标均优于初始调度函数,其中梯级保证率由82%提升至95%,保证出力破坏程度由66%降至48%,从数据上看优化后的调度函数指导梯级调度效果良好。但若在模拟时以
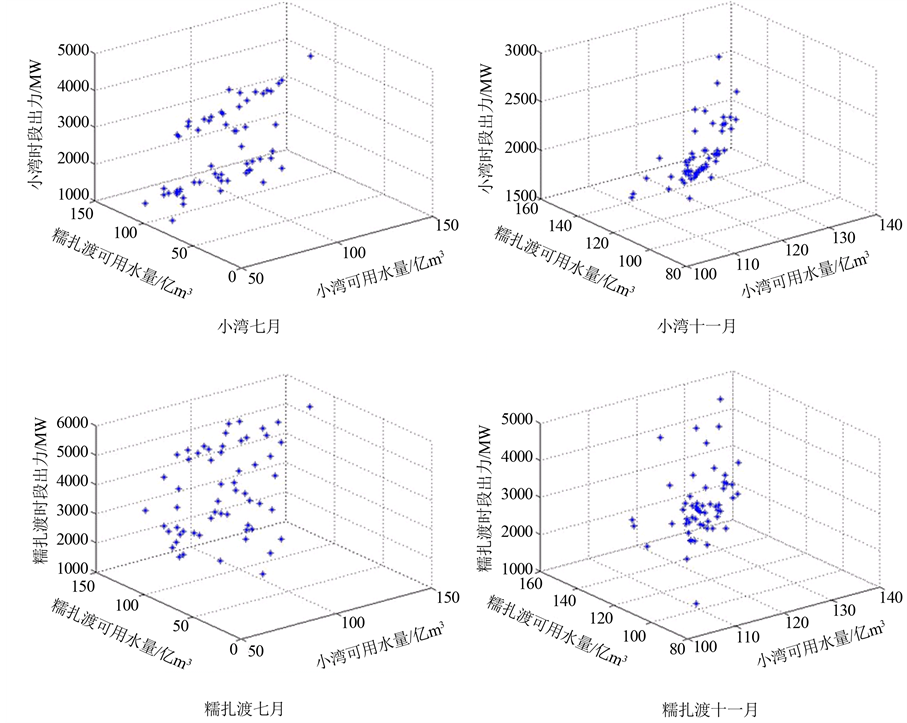
Figure 2. Correlation between time-average output and available water
图2. 出力–可用水量散点图
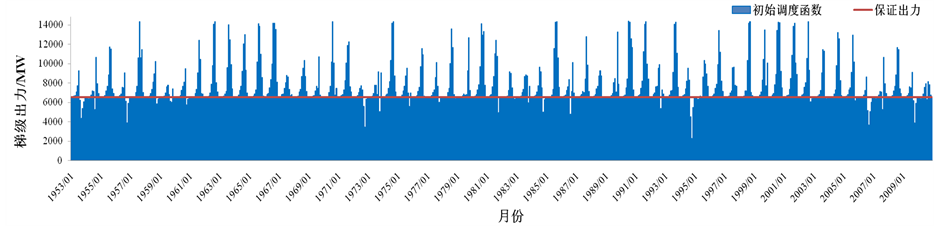
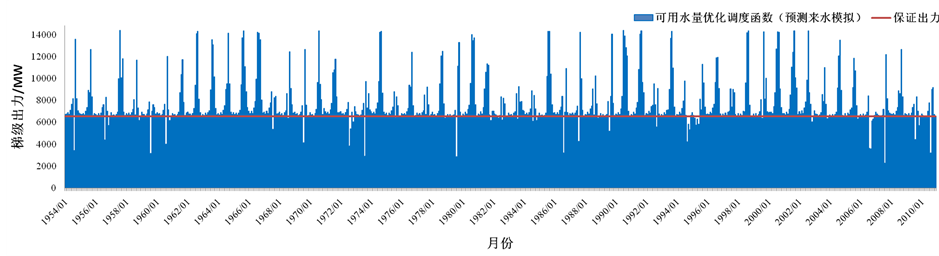
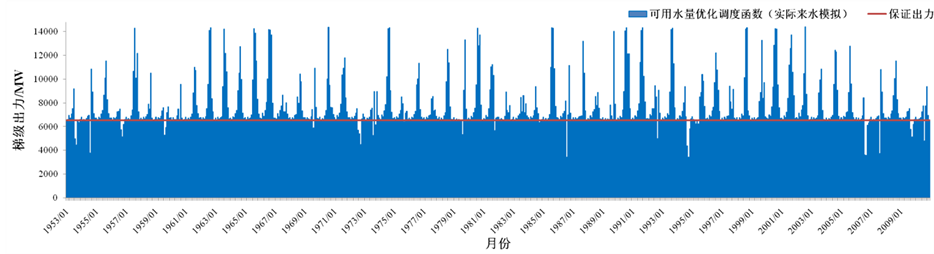
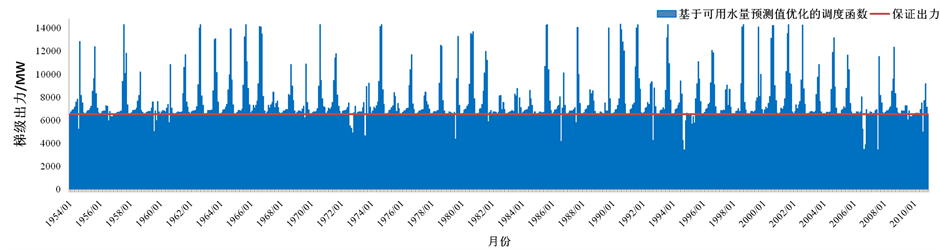
Figure 3. Output figure of cascaded reservoirs
图3. 梯级出力过程图
面临时段来水预报替代历史流量输入调度函数计算决策出力,即采用预测来水代替历史流量检验可用水量调度函数时,梯级保证率有所下降,保证出力破坏程度也由48%升至65%,模拟效果有所降低。可见,来水预报误差对于调度函数模拟调度效果有一定负面影响。为克服这一问题,在调度函数构建和优化过程中以预测来水代替历史流量,以可用水量预测值代替可用水量进行模拟调度和函数评价。对比可以看出基于可用水量预测值优化的调度函数可以有效避免预报误差对调度函数的影响,模拟调度各项效益指标较可用水量调度函数采用预测来水模拟方案时明显提升。
表3为七月和十一月小湾、糯扎渡不同方案下调度函数各项系数具体值,在这两个月里小湾时段决策出力同小湾时段可用水量(或其预测值)成正比,同糯扎渡时段可用水量(或其预测值)成反比;糯扎渡时段决策出力同两库可用水量均成正比。不同方案间糯扎渡可用水量项系数无明显改变,说明初始调度函数中这一项拟合值可调空间较小,在优化精度范围内接近最优值。
图4为基于可用水量预测值优化的调度函数模拟调度水位过程,大多数情况下,小湾优先加大出力补充下游发电用水,而糯扎渡优先降低出力抬高水头,符合本流域调度的特点和规律,进一步说明了调度函数的有效性。
因基于可用水量预测的调度函数应用了预报信息,而预报模型自身存在外推能力问题。为进一步检验该调度函数,将历史流量资料分为两段,1954~1993年40年为率定期,即采用这一期间的径流进行预报模型的参数率定和调度函数优化,1994~2010年17年为检验期,用以检验将预报模型结合调度函数时的外推能力。结果中,率定期年均发电量678.85亿kW×h,保证率96.7%,保证出力破坏程度21.4%,检验期年均发电量663.47亿kW×h,保证率91.2%,保证出力破坏程47.7%。而可用水量调度函数在使用预报来水检验时,相应于率定期的结果为年均发电量679.48亿kW×h,保证率93.8%,保证出力破坏程42.4%,检验期的结果为年均发电量664.18亿kW×h,保证率85.3%,保证出力破坏程60.3%。可用水量预测值调度函数在检验期指标有所下降,但整体仍优于不考虑预报的可用水量调度函数使用预报来水模拟的调度结果。

Table 3. Coefficients of reservoir operation rules
表3. 调度函数系数
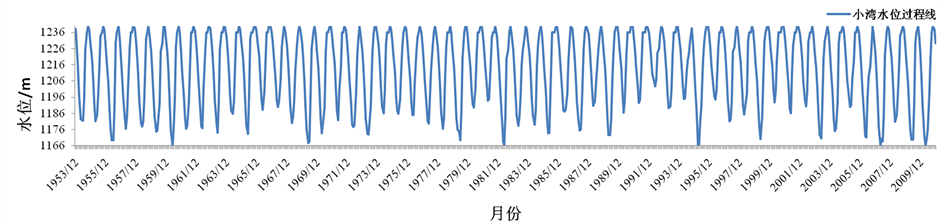
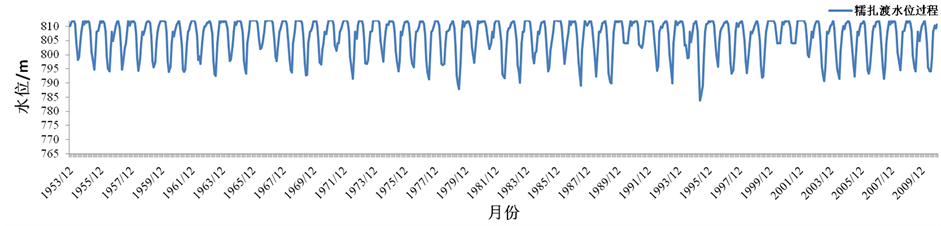
Figure 4. Water level curves of Xiaowan and Nuozhadu
图4. 小湾、糯扎渡水位过程图
6. 结论
针对以可用水量作为状态变量的调度函数在结合来水预测时应用效果欠佳的问题,提出基于可用水量预测值代替历史流量的调度函数及其优化模型。该模型将面临时段初库容叠加来水预测作为可用水量预测值,以此为状态变量构建线性调度函数。在多元回归得到的初始参数基础上,以梯级保证率和保证出力破坏程度约束下多年平均电量最大为目标对初始参数进行优化。澜沧江中下游梯级水库群实例研究表明,本文提出的基于可用水量预测值的调度函数可有效降低预报误差对调度效果的影响,得到优于以可用水量为自变量的调度函数,对结合长期预报的梯级水电站调度规则制定具有一定的指导意义。
基金项目
国家863高技术基金项目(2012AA050205);国家自然科学基金(51109024)。

NOTES
作者简介:王栋(1989-),男,硕士研究生,研究方向:水电优化调度。
*通讯作者。