1. 引言
如何理解复杂网络的演化是当前研究的热点，而链路预测是网络演化中的一个基本问题。由于节点的属性信息难以获取，预测算法的准确率难以得到保证。同时，在现实中不少网络规模较大，增大了计算开销。由于这个原因，基于局部信息的相似性指标的链路预测算法受到了更大的关注[1] 。早期的链路预测研究思想以基于共同邻居的个数为主，即：若两个节点之间存在更多的共同邻居，则该两个节点有更大的可能产生连边。而在共同邻居个数的基础上，根据两端节点度的影响从而逐渐发展出以下指标：Salton指标、Jaccard指标、Sorenson指标、大度节点有利(HPI)指标、大度节点不利(HDI)指标、LHN-I指标[2] 。随后，一种以共同邻居的度值为基础的思路被提出，从而产生了Adamic-adar (AA)指标和资源分配(RA)指标[3] 。
随着研究的不断深入，很多学者注意到不能单纯地考虑共同邻居的个数或其度值，而是应该深入研究共同邻居之间的相互关系，即：若共同邻居之间存在更多的连边，则两端节点属于同一个社区的可能性更大，产生连边的可能性也会更大[4] -[6] 。
通过对10种基于节点局部信息的相似性指标的研究，吕琳媛发现CN指标、Adamic-adar (AA)指标和资源分配(RA)指标算法[7] 比其余算法有较好的准确率[3] 。这三种指标分别定义如下：
(1) CN指标：基于节点局部信息的最简单的相似性指标是共同邻居指标(common neighbors)。该指标定义为两个节点的共同邻居数量，即两个节点之间如果有更多的共同邻居，则更倾向于连接。对于节点i，定义i的邻居集合为Γ(i)，设节点x和节点y的相似性为Sxy，即：
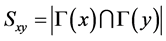(1)
(2) AA指标：该指标考虑的是两个节点的共同邻居的度值信息，其思想为度值小的节点的贡献度大于度值大的节点。因此根据共同邻居节点的度值给每个节点赋予一个权重，该权重为节点度值得对数分
之一：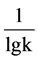
。对于节点i，定义i的邻居集合为Γ(i)，k(i)为节点度值。设节点x和节点y的相似性为Sxy，即：
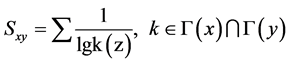(2)
(3) RA指标：该指标是从网络资源分配的角度提出的。考虑网络结构中尚未连接的两个节点x和y，从x传递资源到y。而在传递过程中，它们的共同邻居充当传递的媒介。假设每个共同邻居作为媒介时能将一单位的资源平均分配到它的邻居，则节点x和节点y的相似度为Sxy定义为节点y能接收到从节点x开始传递的资源数。对于节点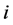
，定义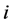
的邻居集合为Γ(i)，k(i)为节点度值。设节点x和节点y的相似度为Sxy，即：
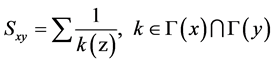(3)
以上三种指标虽然准确率较高，但依然有着一定局限性。CN算法将所有的共同邻居等同看待，仅利用共同邻居的数量作为节点对间相似度的评分函数，没有区分出不同的邻居对链接预测的影响是不一样的；AA算法和RA算法虽然区分了每个不同的共同邻居对链接预测的不同的影响力，但是它们都只关注于共同邻居本身，而忽略了这些共同邻居之间的相互影响。
为了克服这些局限性，本文提出了基于集聚系数的链路预测方法。该算法所基于的假设是，节点的集聚系数越大，则尚未相连的邻接点间存在连边的概率越大。基于这个思想，本文提出一种基于集聚系数的新算法，该算法同时考虑了两端节点以及共同邻居的本身特征，能反应出节点间的相互作用关系。
2. 问题描述
定义G(V,E)为一个无向网络，其中V为节点集合，E为边集合。网络的总节点数为N，边数为M。该网络共有N(N−1)/2个节点对，即全集U。这样，链路预测问题可描述为：构建某种相似度指标，对没有连边的节点对(x,y)计算其相似度Sxy，Sxy越大，节点对(x,y)出现连边的概率越大。
为了衡量算法的精确度，我们将已知连边E分为训练集ET和测试集EP两部分，其中EP为在E中随机抽取的10%的边，剩下的边均匀分配至ET。另外，将属于U但不属于E的边定义为不存在的边。本文使用AUC指标来衡量算法的准确性。AUC (area under the receiver operating characteristic curve)定义为随机在测试集中选取的边的分数值比随机选择的一条不存在的边的分数值高的概率。即每次随机从测试集中选取一条边与随机选择的一条不存在的边进行比较，加分规则如下：若测试集的边的分数值大于不存在的边的分数值，则加1分；若两个分数值相等，则加0.5分；若测试集的边的分数值小于不存在的边的分数值，则加0分。重复以上步骤，独立地比较n次，定义n1为测试集中边的分数值大于不存在的边的分数值的次数，定义n2为两个分数值相等的次数，则定义AUC为：
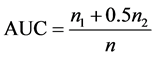(4)
3. 基于集聚系数的链路预测算法
本节提出一种新的基于局部信息相似性的链路预测算法，该算法综合考虑了两端节点以及共同邻居的本身特征，同时由于集聚系数的特性，即它能反应出节点间的相互关系，所以该算法有着更高的参考价值。
集聚系数(clustering coefficient)用来描述一个节点的邻接点之间相互连接的程度，将该系数运用在社交网络中，其意义为该用户的朋友之间也是朋友的概率[8] 。设网络中一个节点i，该节点的集聚系数C(i)等于其邻接点之间连边的数量除以邻接点之间可以连出的最大边数。设ei为节点i的邻接点之间连边的数量，k(i)为节点i的度值，则：
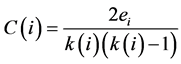(5)
本文认为，节点的集聚系数越大，其邻接点集结成团的概率越大，则尚未相连的邻接点间存在连边的概率越大。因此，本文提出一种基于集聚系数的新算法，该算法在考虑共同邻居数量的同时，还考虑了节点的集聚系数，即对每个参与计算的节点进行赋权，算法中节点x和节点y的相似性定义为Clustering Coefficient(CC)指标：
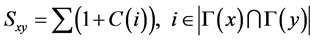(6)
CC算法流程图如图1所示。
4. 实验结果
4.1. 数据集
为对本文所提算法进行测试，本文使用了4种现实网络数据：adjnoun网络、football网络、polbooks网络、US power grid网络以及3种由pajek生成的模拟小世界网络：SW1、SW2、SW3。它们的网络拓扑性质见表1。其中，N和M分别表示网络的节点数和边数，K表示网络平均度，C表示网络集聚系数，r表示网络同配系数，e表示网络效率。
4.2. 实验结果
将CN、AA、RA、CC在7个网络中进行实验，并比较准确率。在AUC测试正确率中，对原始数据集进行了随机抽取分成了训练集(含90%的连边数)和测试集(含10%的连边数)，随后进行了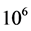
次的随机抽样比较。
4.3. 实验分析
我们使用AUC评价指标，对三种经典方法和本文所提方法进行对比试验，实验结果如表2所示。结
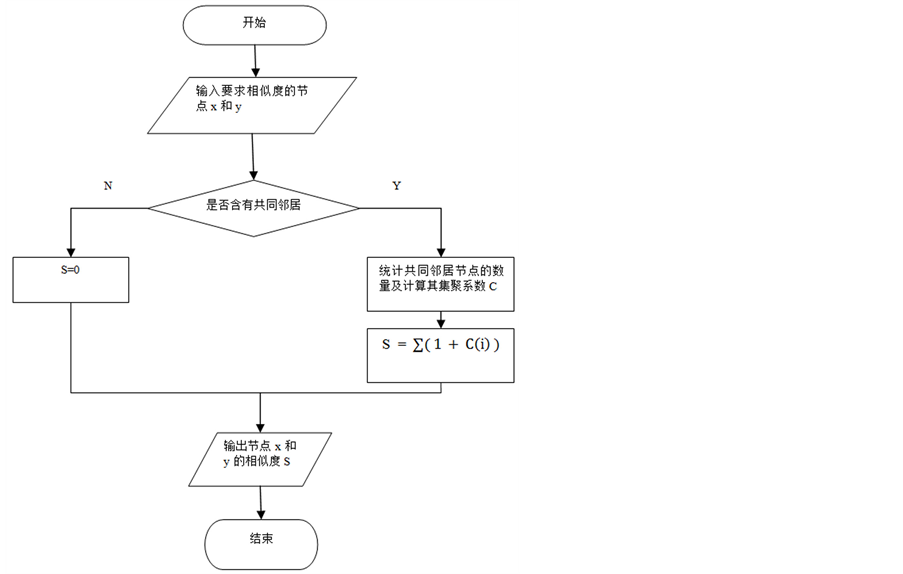
Figure 1. Flowchart of CC
图1. CC流程图
Table 1. Topological properties of seven networks
表1. 7个网络的拓扑性质
Table 2. Experimental result (AUC) n = 1,000,000
表2. 实验结果 (AUC) n = 1,000,000
果表明，本文所提出的CC指标在7种网络中都取得较好的准确度。该指标在adjnoun网络、football网络和US power grid网络中有最高的正确率，在SW1网络和SW3网络有第二的正确率，在polbooks网络和SW2网络的正确率则与其他算法较为接近。从表1的网络拓扑信息中可以发现， 由于US power grid网络和三个模拟生成的网络均具有较低的网络平均度和平均集聚系数，因此局部信息相对较少，从而影响到指标的准确率。总体来看，CC指标在7个网络中表现稳定，且在部分网络中表现突出。
5. 总结
传统的基于局部相似性指标的链路预测方法，主要单独考虑节点相似性或路径相似性因素。为了将二者更好地结合，进一步提高预测算法的准确率与稳定性，本文提出了基于集聚系数的链路预测算法。该法综合考虑了两端节点以及共同邻居的本身特征，能反应出节点间的相互作用关系。我们的实验结果表明：该方法具有准确率高、表现稳定等特点，对链路预测方法及应用有着重要的参考价值。
致 谢
本论文感谢广东外语外贸大学大学生创新创业训练计划项目的支持。