1. 引言
实变函数是数学专业重要的通识基础课。通过学习实变函数,可以培养学生严密的逻辑思维能力和数学的思想方法,运用点集分析方法分析问题和解决问题的能力,为学习有关专业课程和扩大数学知识方面提供必要的数学基础[1] [2] 。而要学好实变函数,首要的问题是要让学生掌握实变函数中的基本概念和基本性质[3] 。根据我们的经验,在实际教学中解决这个问题的一个有效方法是恰当地使用反例。在数学中,要确立一个命题为真,必须在已有的知识之上,经过一系列的逻辑推理予以证明,而要说明一个命题为不真,只需举一个与命题结论不符的例子就够了。这种用来说明某个命题为不真的例子,通常称为反例(counterexamples [4] )。
2. 实变函数中反例的常见类型
2.1. 一些简单命题的反例
例1:任意多个开集之交集未必为开集。
【反例】设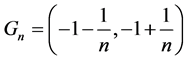 ,
,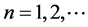 ,每个
,每个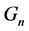 为开集,但
为开集,但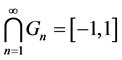 不是开集。
不是开集。
例2:若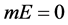 ,则
,则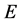 未必是可数集。
未必是可数集。
【反例】设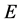 是Cantor集,则
是Cantor集,则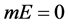 ,但
,但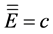 ,故
,故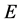 为不可数集。
为不可数集。
2.2. 改变命题条件得到的反例
实变函数中有许多数学命题,其条件有多个,当条件发生改变(增加、减少或变换)时,导致命题不真的反例就是改变命题条件得到的反例。
例1:【命题】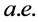 收敛的函数列必依测度收敛。
收敛的函数列必依测度收敛。
【分析】命题错误。因为Lebesgue定理要求必须有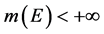 这个条件。
这个条件。
【反例】取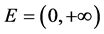 ,作函数列:
,作函数列: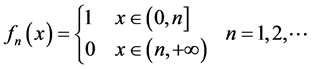
显然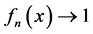 ,当
,当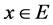 。但当
。但当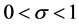 时,
时,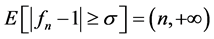 ,且
,且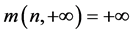 这说明
这说明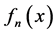 不测度收敛到1。
不测度收敛到1。
例2:【命题】对于任意可测集合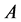 ,
,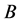 ,如果
,如果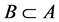 则有
则有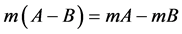 。
。
【分析】命题错误。如果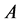 ,
,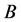 都是测度无限集合,显然结果不成立。
都是测度无限集合,显然结果不成立。
【反例】任何测度无限集合的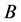 都可作为反例。
都可作为反例。
2.3. 逆命题的反例
例1:【命题】若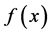 是可测函数,则
是可测函数,则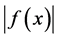 必是可测函数。
必是可测函数。
【逆命题】若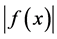 是可测函数,则
是可测函数,则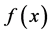 必是可测函数。
必是可测函数。
【反例】设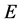 是
是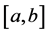 上的不可测集,
上的不可测集,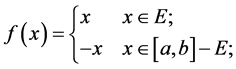
则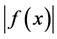 是
是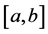 上的可测函数,但
上的可测函数,但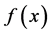 不是
不是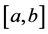 上的可测函数。
上的可测函数。
例2:【命题】如果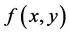 Lebesgue可积,则
Lebesgue可积,则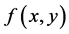 的两个累次积分存在且相等。
的两个累次积分存在且相等。
【逆命题】如果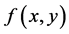 的两个累次积分存在且相等,则
的两个累次积分存在且相等,则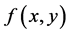 Lebesgue可积。
Lebesgue可积。
【反例】设
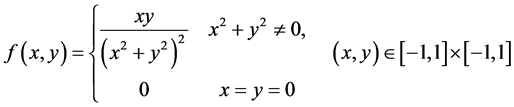 则虽然
则虽然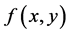 的两个累次积分存在且相等,但
的两个累次积分存在且相等,但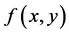 Lebesgue不可积。
Lebesgue不可积。
3. 反例在实变函数教学中的作用
3.1. 有助于让学生准确理解基本定义
通过运用反例,常常能从反面消除一些容易出现的模糊认识,有助于让学生严格区分那些相近的、易混的概念,抓住概念的要素和本质,从而达到较好的教学效果。
例如:集合的基数的定义比较抽象,通过举反例可以加深学生对此概念的理解。如有的学生观察到有限集合不能与其真子集合具有相同的基数,就据此得出任何集合不能与其真子集具有相同基数的结论。此时,我们给出整数集合和它的真子集自然数集合的基数相同的反例。通过这个反例不仅加深了学生对集合基数的理解,而且也让学生看到了有限与无限的本质区别。
3.2. 有助于让学生正确掌握基本定理和命题
在实变函数的定理和命题教学中,运用生动的反例驳斥错误是非常有效的。反例可以用来说明真命题的适用范围,这对于初学者是非常有帮助的,不仅能澄清一些错误的认识,对基本定理和命题作出正确的理解,也能促使学生形成严密推理和重视条件的习惯。
例如: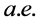 收敛的函数列未必几乎一致收敛。
收敛的函数列未必几乎一致收敛。
取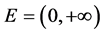 ,作函数列:
,作函数列: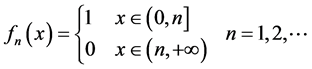
显然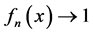 ,当
,当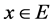 。
。
另一方面:
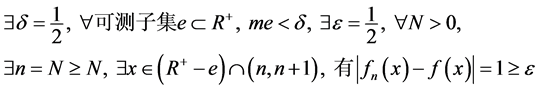
这个反例让学生对叶果洛夫定理的条件“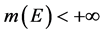 ”的重要性有了清醒的认识。
”的重要性有了清醒的认识。
3.3. 有助于纠正学生错误的认识,激发学生探讨问题的兴趣
举反例和证明是数学的两大重要思维方式。学生在实变函数学习中的创造性,常常离不开直觉思维,但因为直觉思维不够严谨,所以仅凭直觉所得的猜想可能伴有错误。此时,教师引导学生在学习的过程中发现反例,就可以纠正猜想中可能带来的错误。
学生在某一学习阶段,因为受过去认知的习惯性影响,对当前事物的认知容易产生思维定势。教师可根据学生的心理特点,抓住机会恰当地运用反例,消除学生的思维定势,激发学生探讨问题的兴趣。
例如:学生受Lebesgue积分可看作是Riemann积分的推广的影响,总认为Lebesgue积分也能看作是非正常Riemann积分的推广,但事实上可举反例来否定。
例如: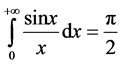 ,但是相应的
,但是相应的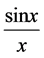 在
在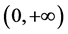 上却不是Lebesgue可积分的。
上却不是Lebesgue可积分的。
3.4. 有助于培养学生的思维能力
3.4.1. 有助于培养学生思维的严密性
例如:命题测度有限集上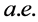 有限的非负可测函数Lebesgue可积。该命题不成立。一般只能说积分
有限的非负可测函数Lebesgue可积。该命题不成立。一般只能说积分
确定,只有当积分有限时才叫做可积。可以举反例: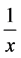 在
在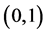 上却不是Lebesgue可积的。通过这样引
上却不是Lebesgue可积的。通过这样引
导学生举反例,就有助于培养学生思维的严密性。
3.4.2. 有助于培养学生思维的发散性
实变函数教学中可经常选择一些需要较强发散性思维的典型问题,通过创设问题情景,引导学生构造反例,鼓励学生勇于并善于发现问题、提出问题,鼓励并支持学生富有创造性因素的思维活动,从而培养学生思维的发散性。
例如:刚刚上面的反例除了可以举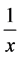 在
在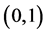 上,还有没有其它的反例呢?通过分析我们知道任何有
上,还有没有其它的反例呢?通过分析我们知道任何有
限集上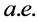 有限的非负无界可测函数都满足要求。显然这样的反例有无穷多个。
有限的非负无界可测函数都满足要求。显然这样的反例有无穷多个。
3.4.3. 有助于培养学生思维的深刻性
例如:由于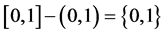 ,故有学生就认为不存在使
,故有学生就认为不存在使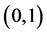 和
和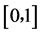 之间
之间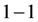 对应的映射。我们记
对应的映射。我们记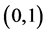 中有理数全体
中有理数全体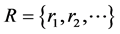 ,
,
令
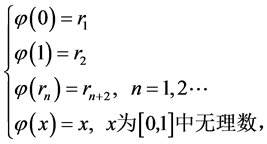
则显然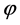 是
是 到
到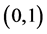 上的
上的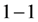 映射。通过这样引导学生举反例,就有助于培养学生思维的深刻性。
映射。通过这样引导学生举反例,就有助于培养学生思维的深刻性。
3.4.4. 有助于培养学生思维的灵活性
反例在剖析错误上具有直观性强、说服力强等显著特点,重视反例教学不仅能使学生发现错误,而且还可以完善相关知识,学会从多个角度思考问题,从而培养学生思维的灵活性。
例如:有学生认为连续函数一定是有界变差函数。可以举反例: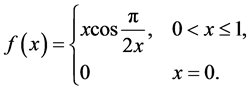
显然是 上的连续函数。如果对
上的连续函数。如果对 取分划
取分划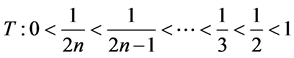 ,则容易证明
,则容易证明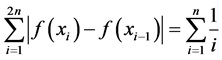 ,从而得到
,从而得到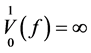 。
。
基金项目
嘉兴学院教改项目(85151325),国家自然科学基金项目(11301225)。