1. 引言
本模板图形(或图像)在计算机里主要有两种存储和表示方法，分别是矢量图和位图。位图虽然内容丰富，应用广泛，但是占用空间大、一旦放大后会产生较为明显的模糊，线条也会出现锯齿边缘等现象，可能会失去图像原有的边缘拓扑结构，失真大；矢量图 [1] [2] 虽然占用的空间小，放大失真小、效率高，但是矢量图大都依靠AutoCAD等软件绘制成，生成的图形简单，绘制时间长，较复杂的图形，要用某些软件进行轮廓勾画，过程很繁琐。
李学营 [3] 、梁雄贵 [1] 等都研究了位图矢量化的相关问题，使用了如模板匹配细化算法、滤波处理算法等多种方法，但分别对圆弧线条和交叉区域处理效果不好，且算法构造复杂，涉及知识和工具过于专业，不易推广。
针对以上存在的问题，本文研究了一种位图转化为矢量图的算法流程，该流程主要分为两大部分：一、图像边缘分割与检测。包括图像分割，灰度处理，二值化处理等；二、图像边缘多项式拟合处理。基于细化的矢量化的方法，得到拟合后的边界线条的数学表达式，利用数学方程完整反映原有图像的边缘结构。利用上述思路，本文先对形状简单的位图转为化矢量图的处理算法进行了研究，得到了比较好的结果。为了验证该算法流程的可行性，我们给出具体的图片矢量化例子，利用MATLAB编程对边缘进行提取，再对结果进行数值模拟，得到了拟合后的边界线条的数学表达式和准确的矢量化图像。
最后将算法推广到复杂的几何图形，发现对梯形边界像素的提取存在一定的误差，为了能准确提取各种图像完整的边缘，我们对模型进行了改进，按Freeman链码 [1] 的8个数字0，2，4，6，1，3，5，7的优先级方向搜索下一个边缘像素点，最后得到了比较满意的边缘提取效果。
2. 系统分析和模型建立
为了系统叙述时减少冗余的解释，通过简单归纳可事先规定，接下来的内容都默认如下事实 [4]
1) 假设边缘分割时产生的噪声干扰对提取边缘像素的影响可忽略不及；
2) 假设图像在局部小的区域内可以看作近乎规则的几何图形。如果图像在某一区域内不规则，我们在局部细化，可以的到规则的小单元；
3) 假设区域内部的像素分布对边缘像素的提取没有影响；
4) 假设简单图形在边缘提取过程中不存在偏转程度很大的点。
为了能够尽可能准确的提取图像边缘的像素信息，我们在传统的特征曲线提取方法 [5] 的基础上进行改进，得到了新的特征曲线法。特征曲线的提取一般分为两个过程：
1) 边界信息提取，即常见的边缘检测；
2) 对检测出的边缘信息进行拟合。
该方法结合了滤波与聚类算法 [5] ，既保证矢量化信息中尽可能受到少的噪音干扰，又能保证图像的主要特征曲线突出，保证了特征曲线信息的完整性，简单有效的实现了对图像矢量化信息的提取。
2.1. 边缘分割与检测
图像分割是成功进行图像分析、理解以及描述的关键技术，图像分割结果的质量直接影响其后进行的分析、识别和解释的质量。图像分割的方法很多，通常可以分为三类：区域分割、边界分割、边缘分割。由于我们假设区域内部的像素分布结构对边缘位点的提取没有影响，下面我们主要对图片进行边缘分割，即首先确定物体边缘像素，然后将所有的边缘像素连接，以便构成所需要的边界，进而实现图像分割。具体算法如下：
1) 对待处理的位图进行图像去噪，保证提取出的矢量化信息准确，不受噪声的干扰。如果图像包含了噪声，就会产生很多假边缘，不利于边缘矢量化，所以要进行图像去噪处理。将图片转化为灰度图像。如果遇到彩色的图像，先把彩色图像变为灰色图像；
2) 将灰度图像转化为二值图像。可能有些图像的一些边缘模糊或不清晰，可以使用灰度变换的方法先将图片边缘改善，再选取好阈值，得到二值化图像。
3) 提取图像边缘的有效位点，其具体算法如下：
①获取图像的边缘；
②把边缘曲线进行矢量化获取边缘曲线的坐标；
③判断图片边缘宽度的像素数目，如果边缘宽度为多像素则转④，否则转⑤；
④对图像边缘进行细化处理，再转①；
⑤将该边缘坐标存入有效位点矩阵，如果边缘点已全部搜索完，则跳出循环，否则转①。
如下所示对图1处理后的效果图的对比：(图1~图4)
Figure 4. Boundary coordinates point set
图4. 边界坐标点集
经过MATLAB编程实现后发现，对于类似上面的简单图形，都可以用上面的算法提取到准确的边界坐标曲线，但对于出现突出的地方，即在局部出现不光滑处，如果细化过程将会很复杂，程序模拟过程相对比较复杂，对于突出区域我们则采用下面方法提取边缘的有效位点。
Freeman链码 [1] 的8个数字的含义包含方向和长度：0，1，2，3，4，5，6，7分别表示的方向为0˚, 45˚, 90˚, 135˚, 180˚, 225˚, 270˚, 315˚。偶数码代表对应的线段为1个，奇数码代表对应得线段为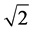
。如下图5(a)是图4中边界坐标点集的局部点集，图5(b)是对图5(a)经过上述Freeman链码法处理的效果实例。
我们借用Freeman链码 [1] 的思想对不规则边缘处的像素点进行追踪，具体算法如下：
1) 按从上到下，从左到右的顺序，搜索第一个为边缘点的像素，找到后存入有效位点矩阵并标记，再以该点为跟踪边缘曲线的起始点；
2) 沿起始点出发，按右上、左上、左下、右下的顺序来搜索下一个像素为1边缘；
3) 如果存在，记下该点的坐标存入有效位点矩阵，并对已经搜索过的点进行标志，防止进入死循环，则以新的边缘点作为后续点，继续搜索下去；如果没有，则结束本次搜索，转1)；
4) 判断所有像素是否都被搜索标记，如果没有，转1)；否则跳出搜索。为了说明算法的可行性与稳定性，我们基于该算法利用MATLAB编程对下图6(a)进行了边缘追踪，得到边界图如下图6(b)所示。
2.2. 边缘多项式拟合处理
目前存在的图片矢量化的方法很多，我们结合基于细化的矢量化的方法，得到拟合后的边界线条的数学表达式，利用数学方程完整反映原有图像的边缘结构，其算法如下：
1) 对找出来的边界点坐标，按勾绘图像边界的顺序进行排序；
2) 按着勾绘图像边界的顺序找出拐点；
3) 对任意边界点坐标，若在其x轴上的点总数介于其x − 1轴上的边界点总数与其x + 1轴上的边界点总数之间，则该点为要找的拐点；
4) 按找到的拐点顺序将边界点坐标分集，即按勾绘图像边界的顺序，将边界点坐标按拐点先后找的顺序分集(先后找的两拐点间的坐标点作为一个集合)；
5) 在每个集合里进行多项式拟合处理，将多项式化为方程；
(a) (b)
Figure 5. Process of edge tracking (1): (a) Boundary points; (b) edge curve got by tracking
图5. 边缘追踪过程(1)：(a) 边界点；(b) 跟踪的边缘曲线图
(a) (b)
Figure 6. Process of edge tracking (2): (a) Original image; (b) Edge curve got by tracking
图6. 边缘跟踪过程(2)：(a) 原图像；(b) 跟踪的边缘曲线图
6) 得图像边界方程组，根据数学表达式画出图像的矢量图。
下面我们利用MATLAB软件编程对几组简单图片进行了处理：
l 图片算例一：(图7)
拟合曲线方程的Monge形式：
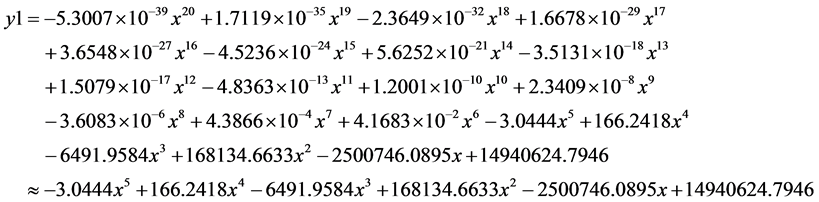
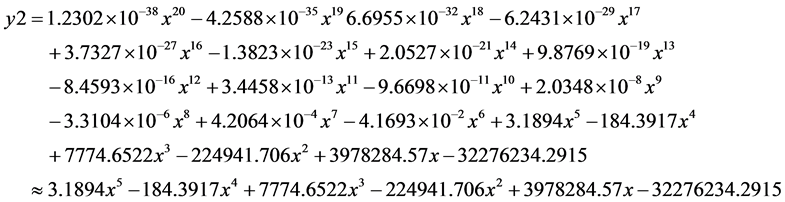
则算例一的拟合数学方程为:
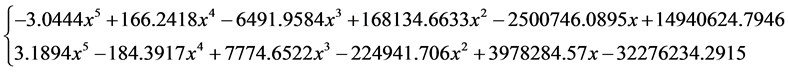
l 图片算例二：(图8)
拟合数学方程为：
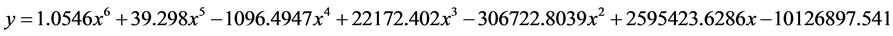
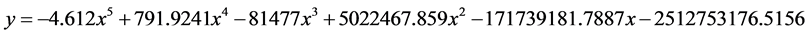
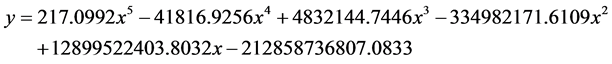
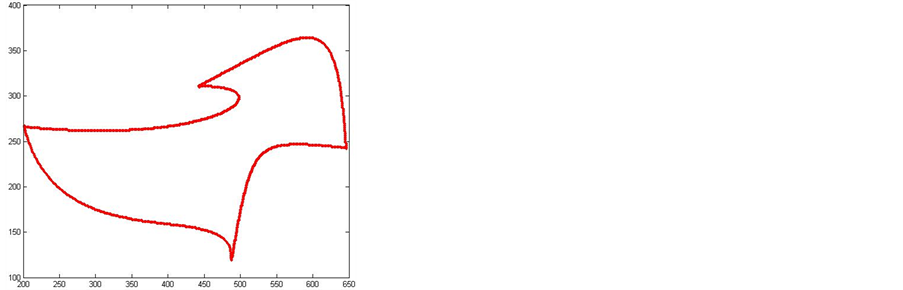
Figure 7. Polynomial fitting of image example No. 1
图7. 图片算例一的多项式拟合
(a) (b)
Figure 8. Polynomial fitting of image example No. 2: (a) Original image; (b) Boun- dary and polynomial fitting
图8. 图片算例二的多项式拟合：(a) 原图片；(b) 边界和多项式拟合对比
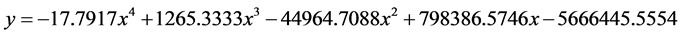
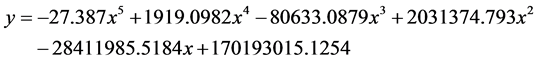
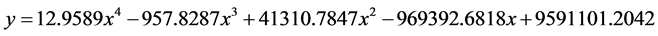
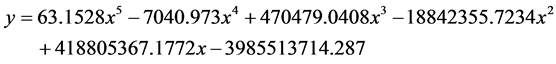
l 图片算例三：(图9)
拟合数学方程：
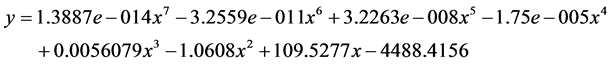
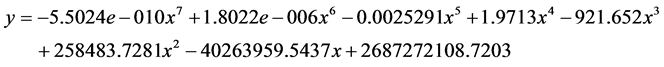
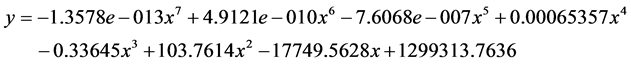
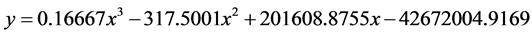
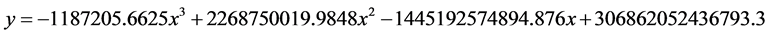
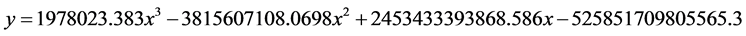
(a) (b)
Figure 9. Polynomial fitting of image example No. 3: (a) Original image; (b) Boundary and polynomial fitting
图9. 图片算例三的多项式拟合：(a)原图片；(b)边界和多项式拟合对比
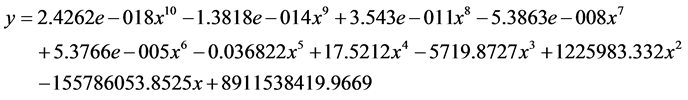
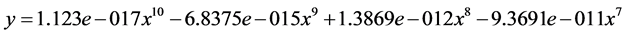
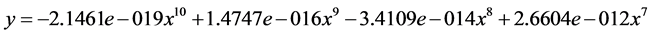
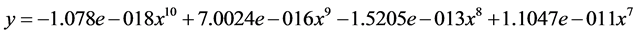
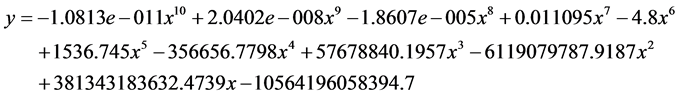
3. 模型分析
通过上面三个图片算例的结果分析可知：对于简单边界的图形，利用上述算法处理的效果令人满意，但图形边界一旦复杂，不论边界的提取还是后期的多项式拟合，结果都不是很理想。这说明了上述算法的局限性，有待深入的分析和改进。
而上述算法步骤1详细过程应扩充为如下结构：
1) 先在边界点像素坐标中找一点，当且满足在以其为中心的九宫格中，以其为中点连接三个相邻点(如图10所示8角线)，只有一条线上满足二值像素排列为
0-1-1
，并记下该角方向；
2) 然后按勾绘图像边界的顺序向下一像素点沿着上点的角方向找二值像素
0-1-1
。
3) 若找到则记下该点，并继续执行2)；若没有找到则顺时针旋转45˚到下一角线上找二值像素
0-1-1
；直至结束。
以上提出的法算法简单，编程不太困难，如上述若干算例中通过Matlab编程处理都得到了比较满意的结果。而且由于所使用的概念简单易懂，描述的过程清晰明了，对专业知识要求不高，该算法实用性较强，利于推广使用。但是其抗噪能力差，对于边缘过于复杂的图形处理结果可能出现偏差。
4. 模型改进
通过对模型的检验我们发现，模型提取的边界是在假设图片结构很简单，没有复杂的拓扑结构的前
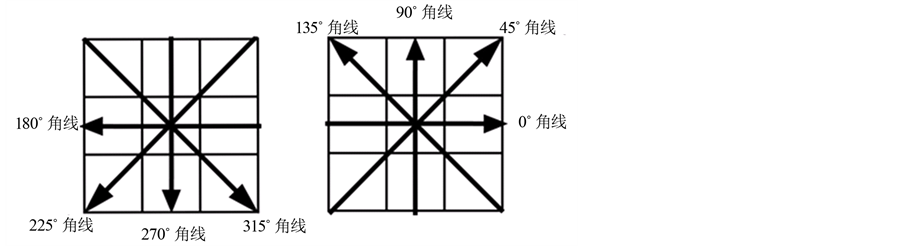
Figure 10. Schematic diagram of the eight diagonal
图10. 8角线示意图
提下得到了很好的矢量化结果，但是对于一般很复杂的结构，模型很可能会失去准确性。而完整的边缘提取是矢量化处理的成功关键，图像边缘的不完整则矢量化的图像就不完整，甚至失真。
下面我们对复杂边界采用高低双阈值的方法 [3] 来实现边缘的检测和连接，设高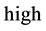阈值为
，低阈值为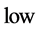
，根据高低双阈值的方法的判断准则为如下：
l 凡是大于高阈值的一定是边缘；
l 凡是小于低阀值的一定不是边缘；
l 如果检测结果大于低阈值且小于高阈值，那根据该像素的邻接像素中有没有超过高阈值的边缘像素，如果有的话那么它就是边缘，否则它不是边缘。
目前图像常见的边缘类型主要分为如下三种 [5] ：阶梯形边缘、屋顶式边缘、线性边缘，它们的类型的结构如图11所示：阶梯形边缘是其的灰度值突然跳到比它高很多的另一个灰度值；屋顶式边缘是其的灰度值慢慢增加到一定灰度值后然后其灰度值慢慢减小；线性边缘是其的灰度值突然跳到一个灰度值后，然后又恢复到原来的灰度值。
在上述模型中我们主要处理的是图像的边缘是屋顶式边缘、线性边缘，但是通过对模型的检验我们发现模型对于阶梯形边缘的下竖线边缘的像素点提取不准确。这是因为上面模型中边缘提取步骤是在不存在拐点的假设下进行的，拐点为该像素的邻近的八像素不止存在一个边缘像素点，但是在实际中，图像边缘存在很多的像素拐点，为了得到完整的边缘跟踪图，就必须对边缘拐点进行一些相应的处理。具体算法如下：
1) 如果该点为拐点，则按Freeman链码 [1] 的8个数字0，2，4，6，1，3，5，7的优先级方向搜索下一个边缘像素点；
2) 记录该点邻近的像素为1的个数和为拐点标志，搜索按优先级的方向的下一个像素点，如果再遇到拐点，则继续保存改点邻近的像素为1的个数和为拐点标志，直到本次的搜索完成；
3) 返回最近的拐点，并以该点为起始点，继续1)，2)；
4) 判断所有保存的拐点搜索是否完成，若完成则结束当前的搜索，否则转1)。
拐点的数据信息包含本像素的坐标、其邻近像素为1的个数、本次搜索拐点总数。边缘点的数据包含本像素的坐标，是否已经被跟踪的标志。上述算法的流程图 [1] 如图12：
我们选取了一个典型的阶梯形边缘且边缘比较复杂的图片,如图13(a)，利用以上算法，得到了跟踪搜索处理的边缘像素点，如图13(b)。简单对比观察可知，此种改进对阶梯形边缘和边缘比较复杂的图片的边缘像素点提取效果比改进之前的算法有明显的提高，对之后的步骤处理效果会有较大的促进。
致谢
本论文的相关研究得到了国家大学生创新训练项目(201310126040)和内蒙古大学大学生创新训练项目(201311140)的资助，特此致谢。此外，在本文的完成过程中得到了内蒙古大学数学科学学院刘洋副教
(a) (b)
Figure 13. A new example: (a) Original image; (b) Edge curve got by tracking
图13. 一个新的算例：(a) 原图片；(b) 跟踪的边缘曲线图
授的大量帮助，在此对刘洋副教授表示衷心的感谢！同时感谢审稿专家和编辑提出的宝贵意见和建议。