1. 引言
岩石是一种或多种矿物的集合体,经历了复杂的结构变动历史,在宏观裂纹出现之前,其内部已经产生了微裂纹及微观空洞,材料中的这些微观缺陷的出现和发展即为损伤。对于岩石来说,其强度理论的核心问题是本构模型。实际上,岩石损伤理论就是研究受损材料的损伤演化规律及其破坏的理论,其核心问题是损伤模型,即确立损伤变量及其转化的问题。
Krajcinovc D等[1] [2] 假设岩石微元强度服从Weibull分布,以轴向应变表示岩石微元强度,建立了特定围压下岩石破裂全过程的损伤本构关系。蒋薇[3] [4] 岩石微元强度服从对数正态分布和二次抛物线型Mohr强度准则,建立了三轴压缩条件下岩石的损伤本构模型。岳洋[5] 基于应变强度理论和岩石微元强度服从幂函数分布的假定,建立了岩石破坏过程中的损伤统计本构模型。谢和平院士[6] 建议用分形几何的方法,用分形维数来沟通微观量与宏观量之间的联系,大大简化分析和计算过程,为岩石类材料的损伤断裂研究开辟了一条新途径。在岩石强度准则方面,许江[7] 、曹文贵[8] 等采用Drucker-Prager准则来表达岩石微元强度,但Drucker-Prager准则是比较保守的,不如Mohr-Coulomb准则和Hoek-Brown准则准确。陈星等[9] 通过分别采用Mohr-Coulomb准则和Hoek-Brown准则模拟卸荷岩体力学性质的试验,表明Hoek-Brown准则描述岩体的破坏模式更准确。总结目前的研究现状,岩石损伤统计本构模型的建立过程就是选择损伤模型、强度准则、岩石微单元强度概率模型的过程,关键点是选取三者的计算公式。目前不同的学者已经根据不同的强度准则和微单元强度概率模型研究了不同的岩石损伤统计本构模型[10] - [19] ,但是还没有H-B准则与幂函数概率模型组合的岩石统计损伤本构模型。
本文对目前公开常用的微元屈服准则和微元概率分布模型进行了总结归纳,找出了建立岩石统计损伤模型的普遍方法,并借助该方法建立了H-B准则与幂函数概率模型组合的岩石统计损伤本构模型,然后引用实例证明本文所建模型和参数确定方法是合理的。
2. 损伤模型的建立
2.1. 损伤本构关系
根据Lemaitre应变等价性假说[20] ,假定岩石微元破坏前服从广义Hooke定律,可建立岩石损伤本构的基本关系式:
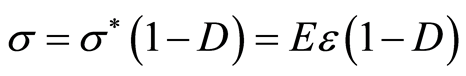 (1)
(1)
式中,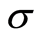 为应力,
为应力,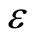 为应变,
为应变,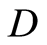 为损伤变量,
为损伤变量,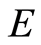 为弹性模量。
为弹性模量。
用有效主应力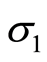 代入式(1),得到三维应力作用下岩石损伤本构方程:
代入式(1),得到三维应力作用下岩石损伤本构方程:
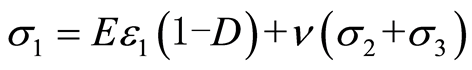 (2)
(2)
式中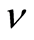 为泊松比。
为泊松比。
显然,确定损伤本构关系的关键是确定损伤变量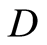 。
。
2.2. 损伤变量
在连续加载过程中,岩石内部微结构一旦损伤便开始表现出不可逆性。损伤的持续扩展,使得岩体各微结构的微元件有效应力不断集中与增大,而局部损伤的发生与扩展又不断削弱岩石的整体承载能力,这反过来又导致其他岩石微元件有效应力继续升高,从而引发新的损伤效应。据刘立等[21] 利用高倍电镜对岩石微结构的观察,岩石内原始微裂隙的分布一般不具有显著的非均匀性。因此,可将岩石内损伤的发生、扩展及力学特征视为一个整体的连续变化过程。
由于岩石是一种非均匀性材料,内含大量随机分布的空隙等缺陷,因此在外荷载作用下,岩石微元件的破坏一般具备随机性,定义损伤变量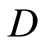 为某一应力水平
为某一应力水平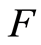 下已经破坏的微元数目
下已经破坏的微元数目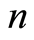 与初始状态下微元总数目
与初始状态下微元总数目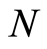 的比值,即
的比值,即
 (3)
(3)
根据岩石的全应力—应变曲线可知,岩石微元在破坏后并非完全失去承载能力,而仍能承受一部分压应力与剪应力,考虑引进修正参数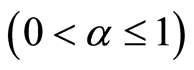
 [22] ,即假定在某一应力水平
[22] ,即假定在某一应力水平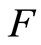 下已经破坏的
下已经破坏的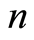 个微元中真正失去承载能力的微元个数为
个微元中真正失去承载能力的微元个数为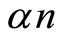 个,则修正后的损伤变量表达式为
个,则修正后的损伤变量表达式为
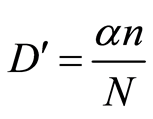 (4)
(4)
在外荷载作用下,岩石微元的破坏是随机的,并注意到Krajicinovic模型,损伤变量就是微元破坏概率,因此可假定岩石微元的破坏概率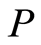 的微元强度分布密度函数为
的微元强度分布密度函数为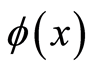 ,则有:
,则有:
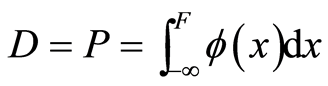 (5)
(5)
由此可看出,损伤变量确定的关键在岩石微元强度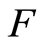 与微元强度分布密度函数为
与微元强度分布密度函数为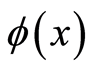 的确定[6] 。
的确定[6] 。
3. 强度准则
岩石的强度准则主要是以岩石的应力状态为依据。近200年来已经提出上百种准则[23] ,但至今普遍适用的强度准则尚未发现。因此,关于它的研究、讨论和应用仍然在不断的发展和创新。目前常用的岩石强度准则有Mohr-Coulomb准则(M-C准则)、Drucker-Prager准则(D-P准则)和Hoek-Brown准则(H-B准则)。
3.1. M-C准则
大量的试验和工程实践已证实M-C强度理论能较好地描述岩土材料的强度特性,因而在岩土工程领域得到了广泛的应用。然而由于M-C准则在三维空间的屈服面为不规则的六角形截面的角锥体表面,在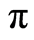 平面上的图形为不等角六边形,存在尖顶和棱角,给数值计算带来困难[24] 。其表达式为
平面上的图形为不等角六边形,存在尖顶和棱角,给数值计算带来困难[24] 。其表达式为
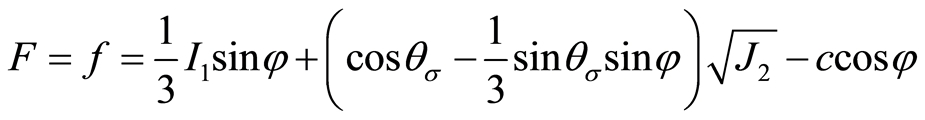 (6)
(6)
式中,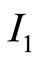 为第一应力不变量,
为第一应力不变量,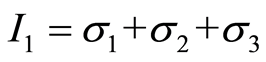 ;
;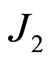 为第二应力偏量不变量,
为第二应力偏量不变量,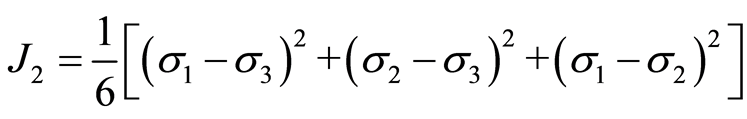 ,
,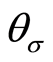 为应力洛德角
为应力洛德角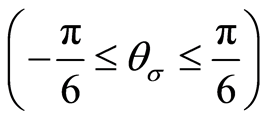 。
。
3.2. D-P准则
D-P准则是在M-C准则和塑性力学Mises准则基础上扩展和推导而来。在主应力空间,D-P准则的屈服面为光滑圆锥,而在 平面上为圆形,这不仅克服了数值计算的困难,且其计算效率相对较高。基于主应力表示的Drucker-Prager准破坏则[7] [25] 为
平面上为圆形,这不仅克服了数值计算的困难,且其计算效率相对较高。基于主应力表示的Drucker-Prager准破坏则[7] [25] 为
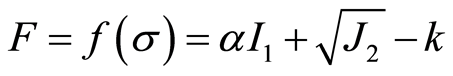 (7)
(7)
式中,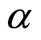 、
、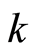 为仅与岩石的内摩擦角
为仅与岩石的内摩擦角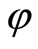 和粘聚力
和粘聚力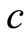 相关的试验常数,计算式如下:
相关的试验常数,计算式如下:
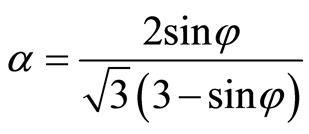
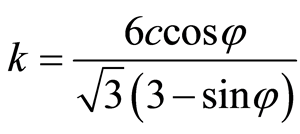
3.3. H-B准则
Hoek等在参考Griffith经典强度理论的基础上,通过大量试验提出了岩体非线性破坏经验准则[9] [26] [27] ,通常称为H-B准则。该准则综合考虑了岩体破碎、岩块强度、结构面强度等影响因素。
采用H-B破坏准则时,岩体微元强度为:
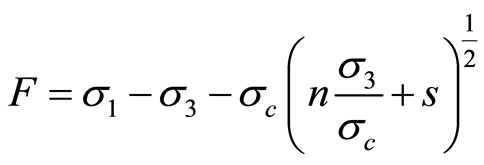 (8)
(8)
式中,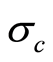 为完整岩体的单轴抗压强度,
为完整岩体的单轴抗压强度,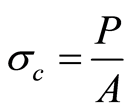 ;
;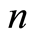 、
、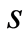 均为与岩体特征有关的常数;
均为与岩体特征有关的常数;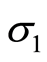 、
、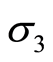 分别为最大、最小主应力。
分别为最大、最小主应力。
4. 岩石微元强度概率模型
根据目前的研究[3] [5] [7] [27] -[29] ,岩石损伤本构模型中常用的微元强度概率模型有Weibull分布、幂函数分布、正态分布、对数正态分布和泊松分布。
4.1. Weibull分布模型
若假定岩石微元强度服从Weibull分布,则其概率密度函数为[7] [28] :
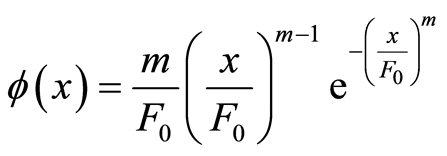 (9)
(9)
式中,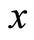 为微元强度的随机分布变量,
为微元强度的随机分布变量,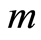 与
与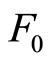 为Weibull分布参数。
为Weibull分布参数。
式(9)代入式(5),得:
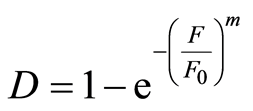 (10)
(10)
4.2. 幂函数分布模型
若假定岩石微元强度服从幂函数分布,则其概率密度函数[5] [29] 为:
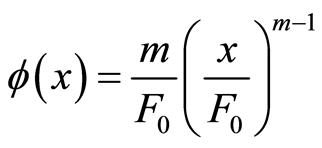 (11)
(11)
式中,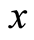 为微元强度的随机分布变量,
为微元强度的随机分布变量,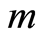 与
与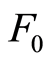 为幂函数分布参数。
为幂函数分布参数。
式(11)代入式(5),得:
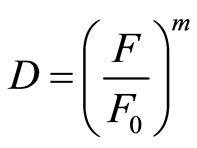 (12)
(12)
4.3. 正态分布
若假定岩石微元强度服从正态分布,则其概率密度函数[3] 为:
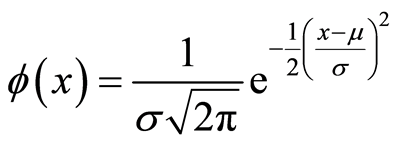 (13)
(13)
式中,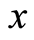 为微元强度的随机分布变量,
为微元强度的随机分布变量,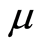 与
与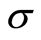 为正态分布参数。
为正态分布参数。
式(13)代入式(5),得:
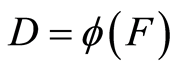 (14)
(14)
式中,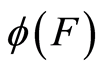 为标准正态分布函数。
为标准正态分布函数。
4.4. 对数正态分布
若假定岩石微元强度服从正态分布,则其概率密度函数[3] [9] [27] 为:
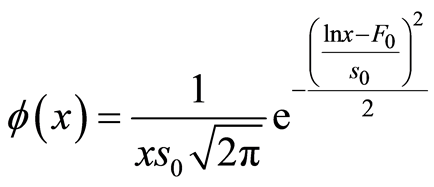 (15)
(15)
式中, 为微元强度的随机分布变量,
为微元强度的随机分布变量,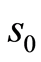 与
与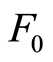 为对数正态分布参数。
为对数正态分布参数。
式(15)代入式(5),得:
 (16)
(16)
式中,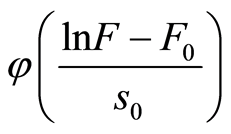 为标准正态分布函数。
为标准正态分布函数。
4.5. 泊松分布模型
唐春安[30] 通过在一维情况下推导,并进行推广得到任意维数情况下服从泊松分布模型的损伤变量表达式
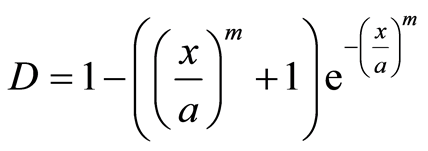 (17)
(17)
式中,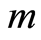 为维数
为维数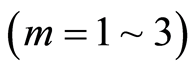 ;
;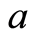 为综合完整度,表示各种缺陷的平均间距(数学期望)。
为综合完整度,表示各种缺陷的平均间距(数学期望)。
5. 统计损伤本构模型
通过以上的文献总结和分析,可以发现目前建立岩石统计损伤模型的普遍方法就是:基于应变等价假设,利用微元屈服准则和微元概率分布模型相结合建立岩石的损伤统计本构模型的表达式,通过实验数据的线性回归确定其中的参数,从而建立岩石的损伤统计本构模型。这其中,由于各自采用的岩石微元强度屈服准则与概率分布函数不同,而出现目前存在的各种不同的岩石损伤统计本构模型。
虽然H-B准则在描述岩体的破坏模式方面更准确,但是它并不能很好的反映岩石强度峰后阶段的软化特征。同时,目前采用微元强度服从Weibull分布假定的较多,而采用幂函数概率分布模型的较少。因此本文试着采用H-B准则与幂函数概率模型组合的模式来建立岩石损伤统计本构模型,一者以实例来说明目前建立岩石统计损伤模型的普遍方法,二者来验证此方法是否合理。具体求解过程如下。
将(4)、(12)式代入(2)式,得:
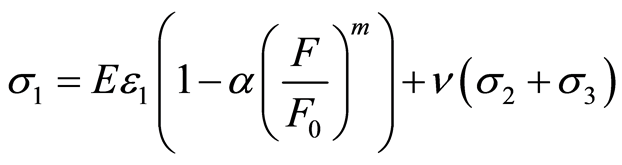 (18)
(18)
将式(8)代入式(18)得
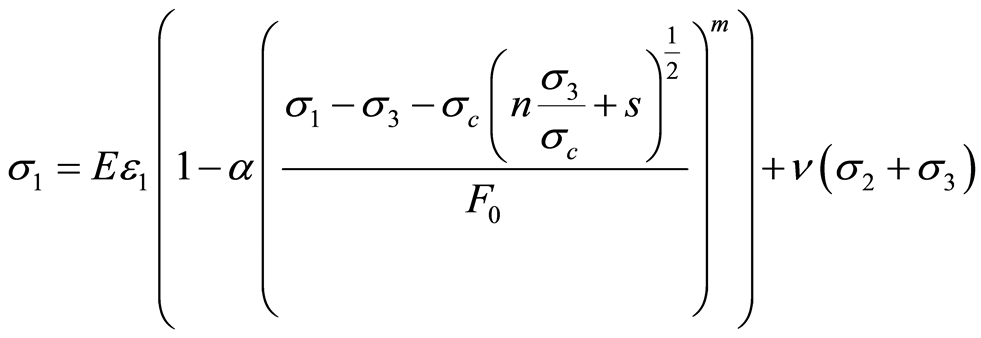 (19)
(19)
至此得到基于H-B准则和幂函数概率模型组合的岩石损伤本构模型,其中含有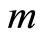 、
、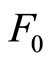 、
、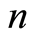 、
、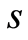 共4个参数。
共4个参数。
对于参数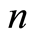 和
和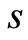 [28] ,由式(8),令
[28] ,由式(8),令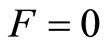 可得
可得
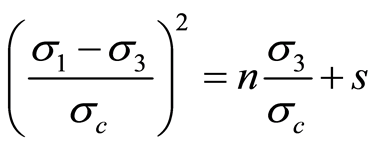 (20)
(20)
令
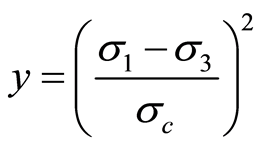 ,
,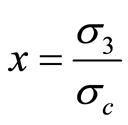
则式(20)可变为
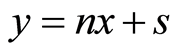 (21)
(21)
通过三轴试验数据的线性回归方法可以确定参数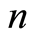 和
和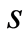 。
。
对于参数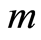 和
和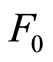 ,将式(19)变形移项整理得
,将式(19)变形移项整理得
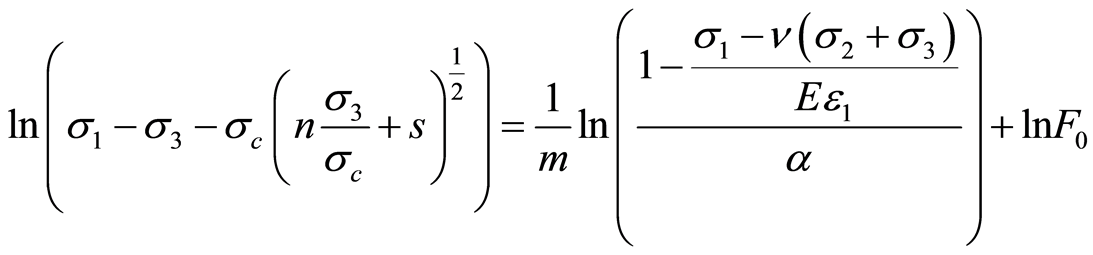 (22)
(22)
令
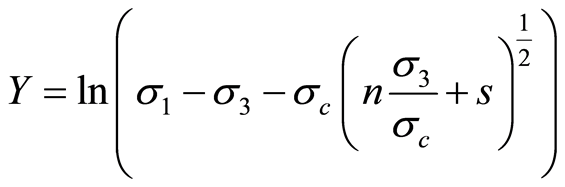 ,
,
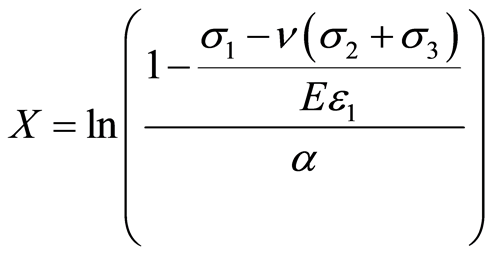
则式(22)变为
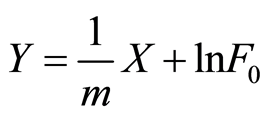 (23)
(23)
通过三轴试验数据的线性回归法亦可以确定参数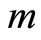 和
和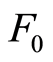 。
。
6. 算例
引用文献[31] 和[32] 中对大理岩的三轴试验资料,岩石弹性模量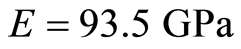 ,泊松比
,泊松比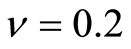 ,粘聚力
,粘聚力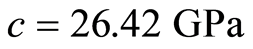 ,内摩擦角
,内摩擦角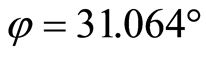 ,在不同围压下岩石的峰值强度值如表1所示。
,在不同围压下岩石的峰值强度值如表1所示。
假定岩体破坏服从H-B准则,计算可得y-x关系如图1,求得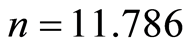 ,
,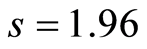 。令参数
。令参数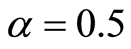 ,同时将参数
,同时将参数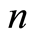 、
、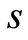 代入式(24),得到Y-X的关系曲线,如图2,则参数
代入式(24),得到Y-X的关系曲线,如图2,则参数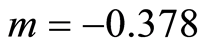 ,
,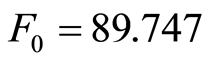 。至此,得到大理岩的损伤统计本构方程
。至此,得到大理岩的损伤统计本构方程

Table 1. Peak strength under different confining pressure
表1. 不同围压下岩石的峰值强度

Figure 1. Obtaining parameters n and s
图1. 参数n、s分析
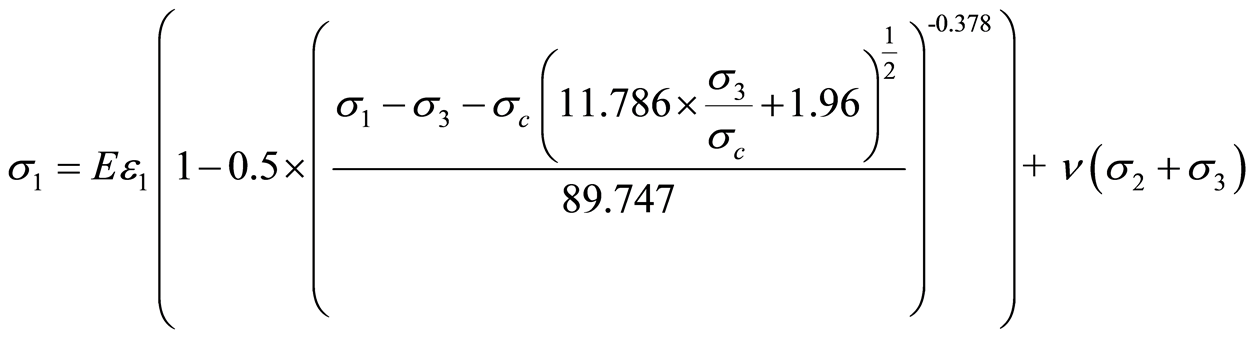 (24)
(24)
根据文献[3] 的数据,在围压为40 MPa情况下,从理论与试验两方面比较岩石的应力–应变曲线,见图3。如图3所示,采用本文所建立的本构模型所得计算结果与试验结果基本吻合,但理论值整体偏大,这主要是由于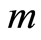 、
、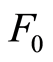 、
、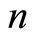 、
、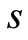 四个参数均采用线性拟合而造成的误差。另外,随着应变的增大,理论计算值逐渐偏离试验值,但应当指出,本文所建立的模型与试验值的最大误差不超过25%,采用本文所建议的方法获取岩石的应力应变关系基本上是合理可行的。
四个参数均采用线性拟合而造成的误差。另外,随着应变的增大,理论计算值逐渐偏离试验值,但应当指出,本文所建立的模型与试验值的最大误差不超过25%,采用本文所建议的方法获取岩石的应力应变关系基本上是合理可行的。
7. 结论
1) 岩石损伤统计本构模型的建立过程就是选择损伤模型、强度准则、岩石微单元强度概率模型的过程,关键点是选取三者的计算公式。
2) 本文所建立的岩石损伤统计本构模型能够较好地描述岩石弹性变形阶段的力学行为,但不适用于描述岩石塑性变形阶段的本构关系。

Figure 2. Obtaining parameters m and F0
图2. 参数m、F0分析
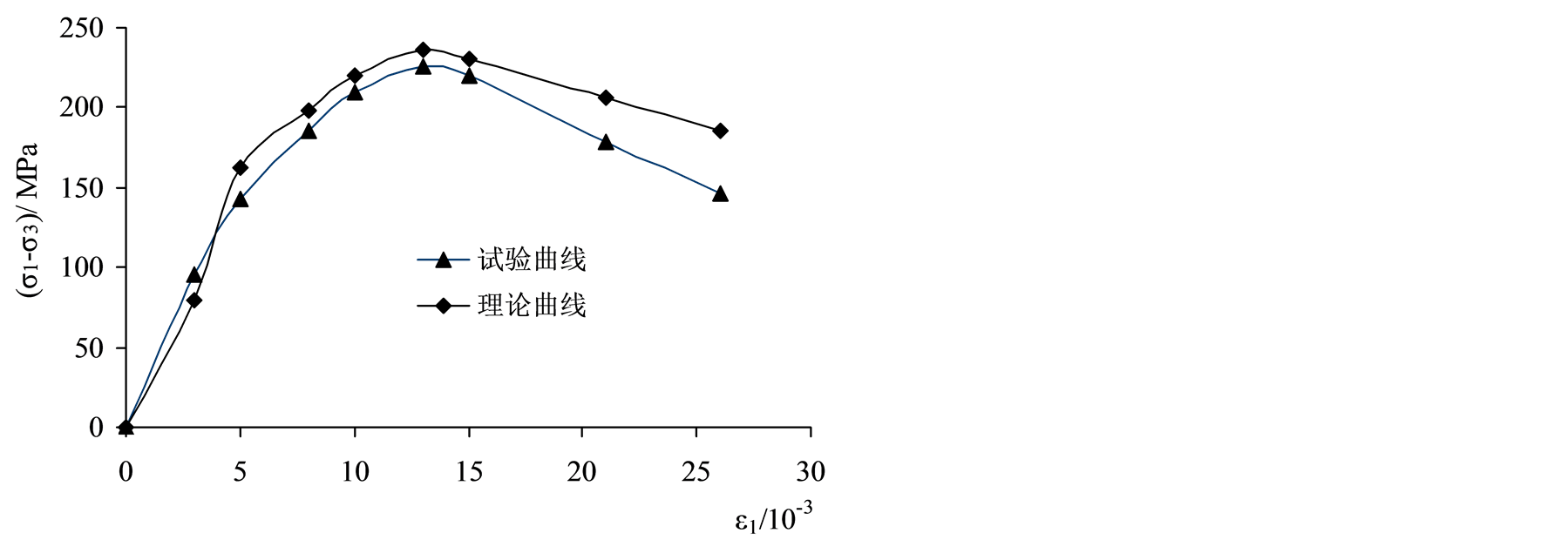
Figure 3. Comparison between analytical results and experimental data
图3. 理论和试验比较
3) 采用统计损伤模型,将连续介质理论和损伤理论有机的结合起来,为岩石类脆性材料的本构模型研究开辟了新途径,但是对于岩石微元强度分布的概率函数形式的系统研究与对比分析需要进一步深入研究。
4) 建立能够反映岩石不同变形阶段力学特性的本构模型,是下一步需要努力的方向,这种模型尤其是要能较为准确的表达峰值后区的残余强度。
致 谢
感谢国家自然科学基金资助项目(40872205)、全国高等学校博士学科专项科研基金资助项目(2012 0171110031)、广东省自然科学基金资助项目(07003738)和广东省科技计划资助项目(2008B030303009)对本论文工作的资助。
项目基金
国家自然科学基金资助项目(40872205);全国高等学校博士学科专项科研基金资助项目(20120171110031);广东省自然科学基金资助项目(07003738);广东省科技计划资助项目(2008B030303009)。

NOTES
*通讯作者。