1. 引言
随着电磁环境的日益复杂，提高雷达的抗干扰性能具有重要意义。雷达的发射信号波形很大程度上决定了信息的类型和信息的质量。目前广泛应用的连续波或周期调制雷达系统都存在距离选择不理想、容易受干扰以及鉴别力差等缺点。随机噪声雷达以微波噪声或噪声调制信号作为发射信号，是一种具有良好抗干扰性能的雷达体制。由于发射信号的随机性及不确定性，随机噪声雷达具有优良的低截获概率、电磁兼容性和电子反对抗性。同时，其模糊函数是理想的“图钉形”，使它具有无模糊测距性能和良好的距离分辨率[1] [2] 。
噪声调制波形具有自身特有的性质，并且接收机通常采用相关处理方式实现，这使随机噪声雷达对其他发射源具有本质的免疫性，即使干扰源同样发射随机噪声，噪声雷达本身仍然不会受到强烈的干扰。与常规系统相比，随机噪声雷达系统的距离和多普勒模糊可以被有效的最小化。此外，随机噪声雷达独有的相关处理有利于低信噪比下的目标检测[3] 。由于存在这些优越性，随机噪声雷达近年来得到迅速发展，它的潜在价值受到世界各国的广泛关注，在军事和民用方面均得到有效应用。
随着分辨率的提高，雷达应用已经扩展到目标成像及地形测绘，形成了各种高分辨率成像雷达并得到了快速发展，成像雷达的出现使原始的雷达概念进一步扩展。合成孔径雷达(Synthetic Aperture Radar, SAR)是一种全天时、全天侯的高分辨率微波成像雷达，它在距离向利用脉冲压缩技术解决了雷达作用距离与距离分辨率之间的矛盾；在方位向利用合成孔径技术突破了天线孔径对方位向分辨率的限制，能够实现远距离目标的二维高分辨率成像[4] 。
随机噪声雷达与合成孔径技术的结合是发展的必然趋势，成像算法的研究是关键。然而，由于随机噪声雷达发射信号的独特性，没有固定的解析表达，因此传统的SAR成像算法并不能直接用于随机噪声SAR成像，因此有必要研究适当的成像算法实现有效的二维聚焦。本文在波数域算法的基础上，研究了适用于随机噪声SAR的成像算法，并分析了在压制噪声干扰的情况下，成像处理的抗干扰性能。
2. 成像原理
SAR成像是通过信号处理的方法得到目标散射强度的空间分布特性。在SAR系统中，场景中的点目标回波信号在距离向与方位向均处于扩散状态，SAR系统的接收过程等效为目标空间到信号空间的一种变换，SAR成像过程是从信号空间为出发点，通过信号处理来完成目标空间的重建[5] ，实现过程如图1所示。
Figure 1. Target imaging process
图1. 目标成像过程
SAR回波可等效为目标的散射特性函数通过二维线性系统的输出，因此对于SAR成像处理，最直接的方法是在时域采用二维移变滤波对回波信号进行直接的匹配压缩。当距离向和方位向的采样点数分别为Nr和Na时，其运算量正比于NaNr2，极其庞大的运算量使得该方法不具有实际可操作性，从而需要提出适用于实际处理的成像算法。在传统成像中，具有较高效率的实用性成像算法有距离多普勒(RangeDoppler, RD)算法、Chirp-Scaling (CS)算法和波数域(ω-k)算法[6] 。
随机噪声SAR将随机噪声雷达系统与合成孔径技术进行了有效的结合，使随机噪声雷达具有了二维成像的能力，同时提高了SAR系统的抗干扰性能。由于随机噪声雷达发射信号的特殊性，使得它具有特殊的距离压缩方式，传统的SAR成像算法不能够直接应用于随机噪声SAR的成像处理过程[7] 。ω-k算法的实现并没有针对发射信号自身的特点，因此传统ω-k算法在针对随机发射信号进行适当的改进后，可应用于随机噪声SAR成像处理。
3. 随机噪声SAR波数域成像算法
3.1. 波数域算法数学模型
波数域(ω-k)算法是利用Stolt插值来消除散射点的距离徙动的影响，校正了SAR成像处理中所有沿距离向的空间移变，包括距离徙动和方位聚焦。理论上，它是SAR回波信号的最优处理。SAR成像系统中的时间变量与空间变量均存在对应关系。设距离向与方位向的空间变量分别为r与x，它们与时间变量的关系为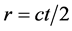
及
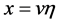。如果直接以变量r与x对回波作傅里叶变换，则进入了二维波数域，即二维频域。在波数域中，方位向角频率
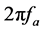与沿方位向的波数kx相对应，它们之间的关系可表示为
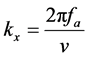(1)
将距离向角频率记作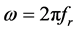
，由于距离徙动的影响，它与距离向的波数kr并不能用类似于式(1)的关系来简单对应，需要通过Stolt变换建立相应的联系。如果方位向以空间为变量，而距离向以时间为变量作傅里叶变换，则称为ω-k域。与RD算法一致，ω-k算法同样是先对回波数据进行距离向压缩，而之后的距离徙动校正与方位向压缩均在ω-k域中完成。将距离压缩后的信号记为sr(t, x)，对它作二维傅里叶变换后为Sf(ω, kx)，即进入ω-k域。根据波动理论，距离向波数kr、方位向波数kx及距离向角频率ω之间的关系可表示为式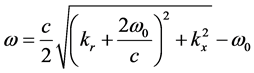(2)
(2)
式中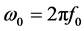
为中心角频率。式(2)即为Stolt变换，为了方便将它记作St(∙)。
在信号空间中由于徙动的影响，ω与kx并不正交。在二维波数域中，kr与kx是正交的，因此以它们为变量进行傅里叶逆变换，即可得到目标空间分布，从而完成二维压缩。先对信号Sf(ω, kx)作Stolt变换，变换后的信号可表示为
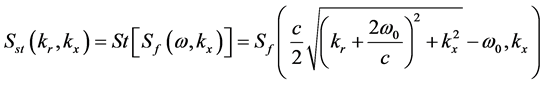(3)
得到信号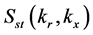
后，对式(3)作傅里叶逆变换则可得到压缩信号
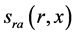，即成像输出，如式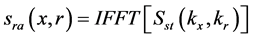(4)。
(4)
实际处理过程中，通常将距离原点设为测绘带中心R0处，这种情况下距离压缩后的ω-k域信号可表示为式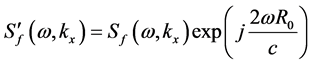(5)。
(5)
对其作Stolt变化后的信号为
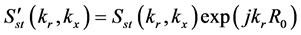(6)
式(5)与式(6)之间的关系如式(7)所示，
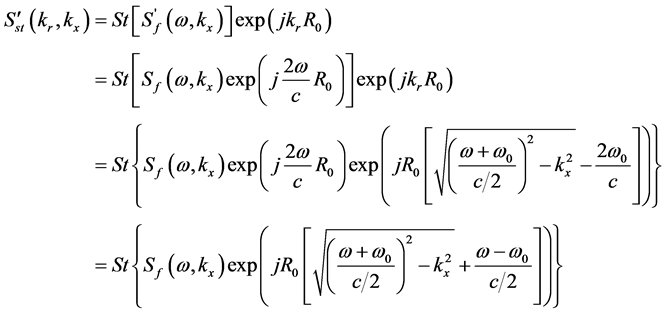(7)
对式(7)作二维傅里叶逆变换，即可得到以R0为中心的目标散射分布。图2所示为本文波数域算法的实现流程，图中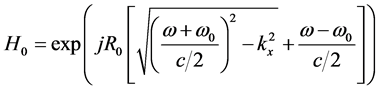
。
3.2. 压制干扰下算法抗扰性分析
压制性干扰有多种形式，射频噪声干扰是其中一种，由于它的电平通常较低，使得射频干扰在实际电子对抗中不常用，但它是干扰信号质量比较及干扰效果计算的基础，因此本节中主要针对随机噪声SAR在射频干扰环境中的成像性能进行分析。
射频干扰也称作纯噪声干扰，它可以直接通过放大微波噪声而产生。对于理想的高斯白噪声来说，它的频谱为均匀无限宽[8] 。由于白噪声的功率很小，用于干扰时要进行功率放大，而功率放大器的带宽
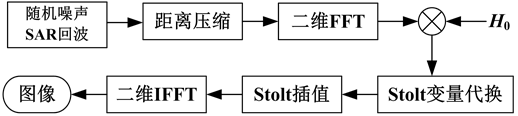
Figure 2. Flowchart of wave domain
图2. 波数域算法实现流程
是有限的，因此干扰信号的带宽通常被设置在雷达的工作频段内，放大后就能够得到射频干扰信号，这说明射频噪声干扰信号是带限高斯白噪声。射频噪声干扰信号可看作窄带高斯过程，它的概率密度为正态分布，其信号模型可表示为式(8)。
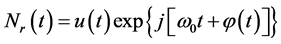(8)
式中
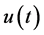与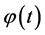
为相互独立，
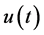为幅度包络，服从瑞利分布；
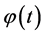为相位函数，服从[0, 2π]的均匀分布；
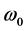为载频，远大于信号
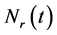的频谱宽度。当产生不同功率的干扰信号时，通常定义干信比(Jamming Signal Ratio, JSR)来衡量噪声干扰的强度，其数学表达为式(9)或式(10)，单位为dB。
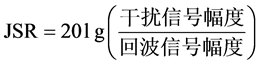(9)
或者
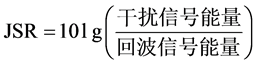(10)
4. 仿真实验
为了验证本文算法用于随机噪声SAR成像处理的效果，给出了相应的仿真实验结果，系统参数的选取如表1所示。
图3所示为9个点目标的ω-k算法成像处理结果，目标均有效的实现了距离向与方位向聚焦。此外，为了直观地评价成像效果，图4给出了只存在图3中圆所标注的点目标情况下，对该点成像后的剖面图，
Table 1. Experimental parameter
表1. 实验参数
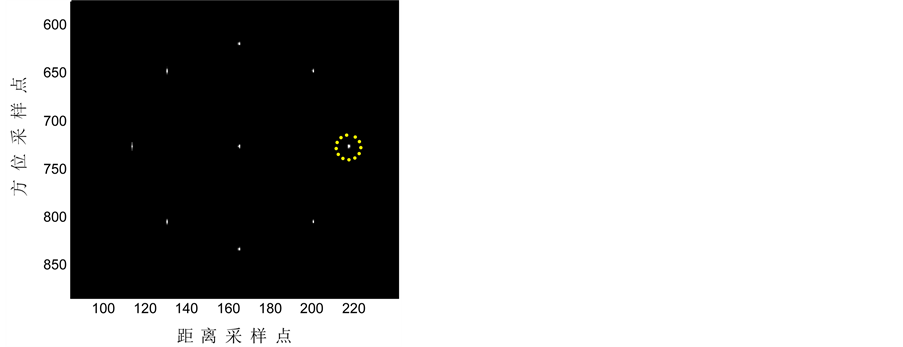
Figure 3. Imaging result of the algorithm
图3. 算法成像结果
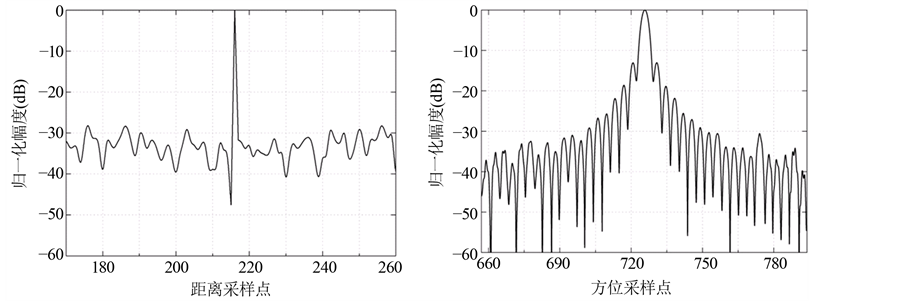
其中图4(a)与(b)分别为距离向剖面与方位向剖面。图4直观反映出点目标的成像效果良好，距离向输出优于传统SAR，方位向输出与传统SAR一致。距离向压缩效果优于方位向，这由随机信号波形所决定。
本文通过仿真实验来分析了成像系统的抗干扰性能，分别在传统SAR及随机噪声SAR成像过程中加入具有式(8)形式的射频噪声干扰，然后分析比较其成像性能。为了区分传统SAR与噪声SAR的成像输出，场景中点目标选取不同的位置。实验中分别利用干信比为40 dB及50 dB的射频干扰信号模拟压制性干扰环境，相应的成像输出分别对应于图5与图6，其中(a)均对应于传统SAR的成像结果，(b)均对应于随机噪声SAR的成像输出。
仿真结果反映出对于传统SAR，当JSR为40 dB时，目标变模糊；当JSR增大到50 dB时，目标基本被干扰信号所覆盖。对于随机噪声SAR的情况，当JSR为40 dB时，目标可以较清晰的分辨；当JSR为50 dB时，目标出现模糊，但仍然能够分辨。图5与图6反映出，存在射频压制干扰的情况下，随机噪声SAR的抗干扰性能较好。
5. 结束语
随机噪声SAR系统依赖于适当的成像算法，而传统的SAR成像算法立足于发射信号为线性调频信
(a) (b)
Figure 4. Image profile of point target, (a) profile of range direction; (b) profile of azimuth direction
图4. 点目标成像剖面图，(a) 距离剖面图；(b) 方位剖面图
Figure 5. Image output at 40 dB radio-interference (a) traditional SAR; (b) random noise SAR
图5. 40 dB射频干扰时的成像输出，(a) 传统SAR；(b) 随机噪声SAR
(a)
(b)
Figure 6. Image output at 50 dB radio-interference (a) traditional SAR (b) random noise SAR
图6. 50 dB射频干扰时的成像输出，(a) 传统SAR；(b) 随机噪声SAR
号时的情况。由于随机噪声SAR的特殊性，传统成像算法并不能直接应用于噪声SAR成像过程中。本文对随机噪声SAR成像算法进行研究，利用波数域算法实现了随机噪声SAR回波的有效处理，获得目标图像。成像性能良好，距离向输出优于传统SAR，方位向输出与传统SAR一致。此外，论文对成像过程的抗干扰性能作了简单分析，通过仿真实验验证了在射频压制干扰环境中，随机噪声SAR与传统SAR相比，具有较强的抗干扰能力。
NOTES
*通讯作者。