1. 引言
汽车的安全性能对人类生命和财产安全的影响是不言而喻的。汽车行驶的安全性很大程度上依赖于横摆和侧倾动力学，尤其是横摆稳定性。横摆稳定性的丧失将使汽车失去转向能力或引起汽车的剧烈回转。汽车失去横摆稳定性是一种高发并且很危险的交通事故。德国奥迪公司的统计数据[1] 表明，在80 km/h到100 km/h的车速下行驶的汽车发生的交通事故中，几乎有40%的事故与汽车失去横摆稳定性有关；随着车速的提高，由汽车失稳引起的交通事故所占的比例也提高，并且当车速超过160 km/h时基本上所有的事故都与汽车失稳有关。因此，通过主动控制提高汽车的横摆稳定性对提高汽车的行驶安全性具有重要的意义。
汽车横摆角速度，作为横摆稳定性的主要控制变量之一，对其进行PID自动控制，这可以明显改善汽车的横摆稳定性，进而有效地提高汽车的行驶安全性。本文研究的基本思路是首先建立基于汽车转向的简化模型——二自由度模型，使其能比较真实地反映汽车的动力学特性；然后，基于模糊控制理论进行PID控制器设计并用Matlab软件建立横摆角速度PID控制器模型；最后在Simulink环境下进行系统仿真。
2. 建立转向线性二自由度汽车模型
汽车横摆角速度控制需要根据方向盘转角信息来判断驾驶员的转向意图，为了便于研究，本文将把汽车作为线性系统来分析讨论.建模时，忽略转向系统的影响，直接以前轮转角作为输入；忽略悬架的作用，认为汽车车厢只作平行于地面的平面运动，即汽车沿z轴的位移，绕y轴的俯仰角与绕x轴的侧倾角均为零。因此，汽车只有沿y轴的侧向运动与绕z轴的横摆运动这样两个自由度。此外，汽车的侧向加速度限定在0.4 g(正常行驶工况下)以下，轮胎侧偏特性处于线性范围。在建立运动微分方程时还假设：驱动力不大，不考虑地面切向对轮胎侧偏特性的影响，没有空气动力的作用，忽略左、右车轮轮胎由于载荷的变化而引起轮胎特性的变化以及轮胎回正力矩的作用。建立线性二自由度的汽车模型[2] 作为汽车横摆角速度控制的参考模型，如图1所示。图中，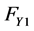
、
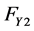为地面对前、后轮的侧向反作用力，即侧偏力；
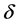为前轮转角；汽车前、后轴中点的速度为
、
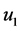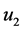；侧偏角为
、
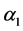；质心的侧偏角为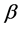
，
；
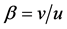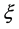是
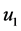与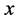
轴的夹角；u为汽车质心沿x轴的前进速度视为不变；v为汽车质心沿y轴的侧向速度。
将汽车的绝对减速度和绝对角加速度及外力与外力矩沿车辆坐标系的轴线分解，就可以列出沿这些坐标轴的运动微分方程。
二自由度汽车的运动微分方程式为
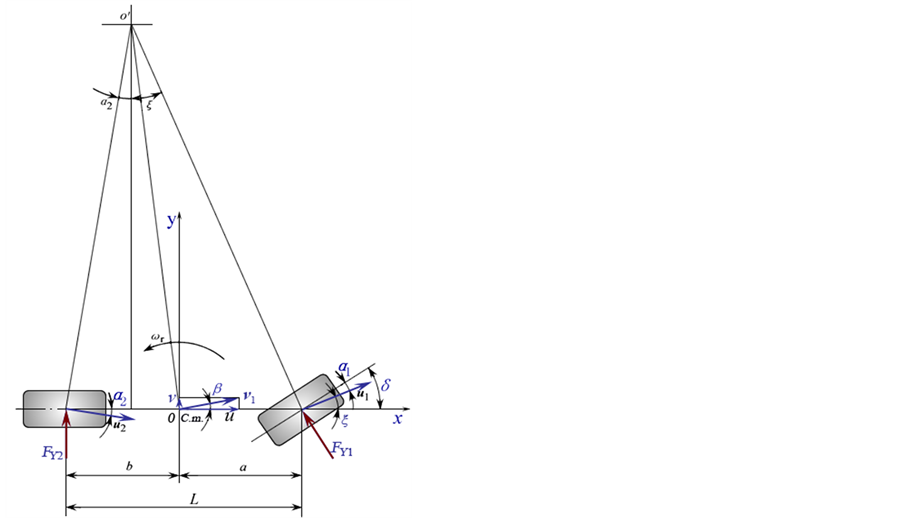
Figure 1. 2-degree of freedom vehicle model
图1. 二自由度汽车模型
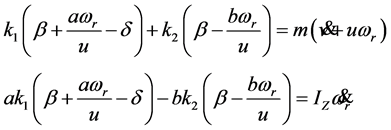(2-1)
式中，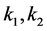
为前、后轮侧偏刚度；
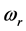为汽车横摆角速度；
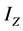为汽车绕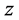
轴的转动惯量；
为汽车总质量。
由上式可推出：
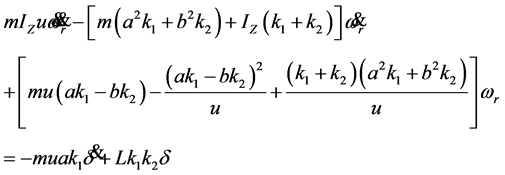(2-2)
将上式整理写成以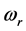
为变量的形式：
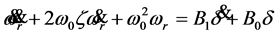(2-3)
式中：
，
；
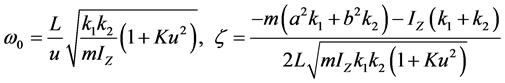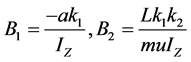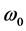为固有圆频率，
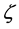为阻尼比。
汽车前轮角阶跃输入时，前轮转角的数学表达式[2] 为：
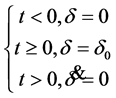(2-4)
当t > 0时，式(2-2)进一步简化为：
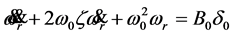(2-5)
将式(2-5)两端进行拉氏变换，整理得线性二自由度模型的传递函数：
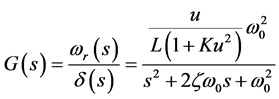(2-6)
其中，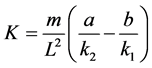
为稳定性因数。
3. 模糊自适应PID控制器设计
3.1. 确定模糊控制器结构
由于受控对象具有非线性与时滞性，为了得到良好的控制性能，我们不仅观测系统的误差e，同时应该观测其误差变化ec的趋势并将其作为输入。将PID个参数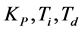
作为输出，因此，本文中选定控制器的结构为两输入三输出的控制器。
3.2. 确定语言变量和语言值的隶属度函数
设定输入误差e的语言变量为E，误差变化率ec的语言变量为EC，两者的论域都为{−3, −2, −1, 0, 1, 2, 3}，相应的语言值为{负大(NB)，负中(NM)，负小(NS)，零(ZO)，正小(PS)，正中(PM)，正大(PB)}；输出比例系数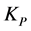
的语言变量为
、积分系数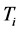
的语言变量为
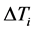、微分系数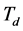
的语言变量为
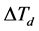，三者的论域都为{−3, −2, −1, 0, 1, 2, 3}，相应的语言值为{负大(NB)，负中(NM)，负小(NS)，零(ZO)，正小(PS)，正中(PM)，正大(PB)}。输入输出变量的隶属度函数均采用三角函数且函数曲线形式相同，如下图2所示。
3.3. 建立模糊控制规则
PID控制算法[3] [4] 是通过三个参量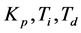
起作用的。这三个参量取值的大小不同，就是比例、积
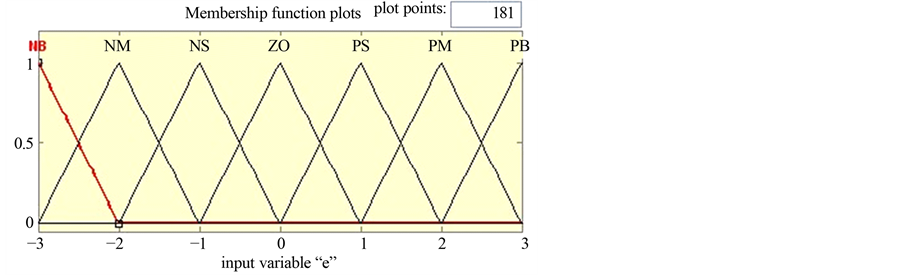
Figure 2. The membership function curve of input variable “e”
图2. 输入变量“e”的隶属度函数曲线
分、微分作用强弱的变化。
比例环节能够及时的成比例的反映控制系统的偏差信号e(t)，控制过程一旦产生偏差，控制器立即产生控制作用，以抑制偏差。在系统稳定的情况下，增大比例系数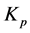
可以提高系统的响应速度减小稳态误差[6] ，却不能够完全的消除误差。系统响应速度的提高使得振荡次数增加，且当比例系数
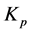太大时，系统的超调量过大，从而降低系统的稳定性，甚至在严重的情况下会导致系统的不稳定。
积分环节主要作用是消除系统静差，提高系统的准确度，以保证实现系统对设定值的误差跟踪。在整定时可先将积分时间常数设定到无穷大，再逐步的减小，不断调试，直到获得满意的控制效果。
微分作用系数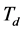
的作用是改善系统的动态特性，其作用主要是在响应过程中抑制偏差向任何方向的变化，对偏差变化进行提前预报。但
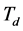过大，会使响应过程提前制动，从而延长调节时间，而且会降低系统的抗干扰性能。
PID控制参数模糊自整定是找出控制器的三个参数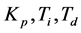
与e和ec之间的模糊关系，在运行中通过不断检测e和ec，根据模糊控制原理来对三个参数进行在线修改，以满足不同e和ec时对控制参数的不同要求，而使被控对象有良好的动、静态特性。当误差e较大时，说明误差的绝对值较大，不论误差的变化趋势如何，都应该考虑控制器的
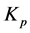取较大值，以提高响应的快速性；而为防止因为ec瞬时过大，
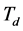应该取较小的值;为控制超调，
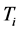也应该取值很小。当误差e在中等大小时，为保证系统的相应速度并控制超调，应减小
，
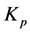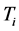值应增大，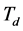
应适中。当误差e较小时，为保证系统具有良好的稳态特性，应加大
、
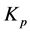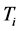的取值，同时为避免产生振荡，e的取值应该和ec联系起来。
按以上原理并根据PID参数自适应原则和操作经验列出输出变量的模糊控制规则如表1所示。
3.4. FIS编辑器设置
在Matlab中调用FIS编辑器进行模糊控制器的编辑，并建立一个FIS文件以便组建控制系统时调用。将输入扩展为二个，将输出扩展为三个。在Membership Function Editor窗口对输入变量e、ec和输出变量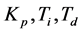
的隶属函数和量化区间进行确立；在Rule Editor窗口按模糊控制规则表建立输入、输出对应的模糊控制规则，共7 × 7 = 49条模糊规则。
4. 模糊PID控制器仿真
4.1. 建立仿真模型
下面将借助某款轿车的部分技术参数如表2所示，取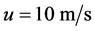
代入二自由度传递函数模型(2-6)式得
Table 1. Fuzzy control rules
表1. 模糊控制规则表
到系统数学模型为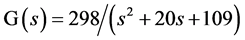
。基于MATLAB的Ziegler-Nichols算法得到该系统控制器参数初值
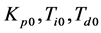。运用上述的模糊控制规则，得到模糊PID的参数：
。
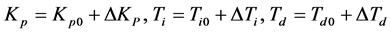图3是基于二自由度汽车数学模型为被控对象的连续系统PID控制Matlab/Simulink仿真程序结构图模型[5] [6] 。由(2-4)式可知，该模型的输入信号为前轮转角单位阶跃输入信号。
其中，模糊PID控制器子系统在Simulink中的封装形式如图4所示。
4.2. 仿真结果
由图5仿真响应曲线可知，模糊自适应PID控制器通过在线自整定具有超调量小、响抗干扰性强的优势。模糊自适应PID控制系统的性能较传统PID控制有明显提高，具有一定的实用价值。但是调节时间改善并不明显，这说明该模糊自适应PID控制技术有待进一步改进。
Table 2. Part of the technical parameters of a car
表2. 某款轿车部分技术参数
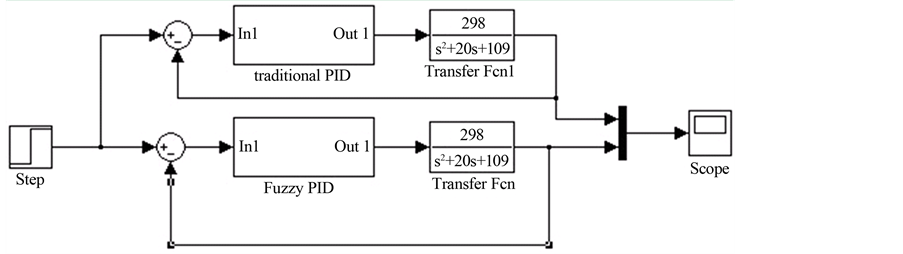
Figure 3. Simulation program structure diagram of continuous PID control system in Simulink
图3. 连续系统PID控制Simulink仿真程序结构图
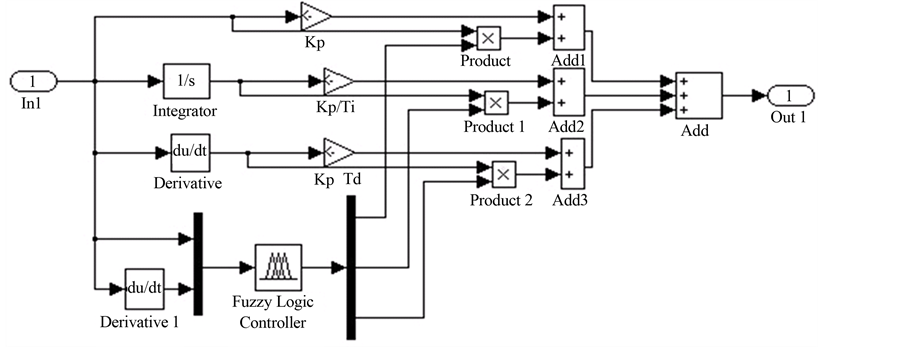
Figure 4. Simulink package of the fuzzy PID controller
图4. 模糊PID控制器的Simulink封装形式
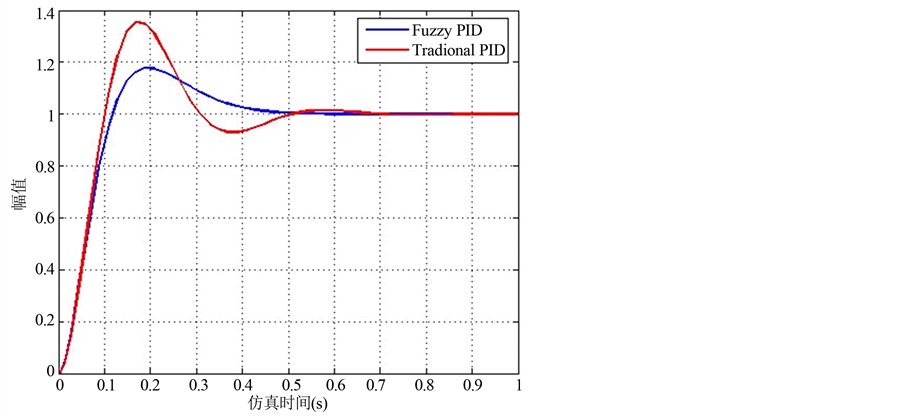
Figure 5. The system response curve
图5. 系统响应曲线
5. 结语
传统PID控制的是经典控制理论中最常用到的控制方法，在传统PID控制的基础上引入模糊控制形成模糊自适应PID控制器是一种比较先进的改善传统PID控制的技术。应用该技术设计基于汽车横摆角速度的模糊自适应PID控制器，有助于完善汽车的主动安全技术，主动预防、避免或减少汽车在行驶过程中发生事故，以提高汽车的主动安全性能。