1. 引言
光子晶体是1987年S. John[1] 和E. Yablonovich[2] 等在研究自发辐射和光子局域化时分别提出的一种周期结构材料。它是由两种具有不同折射率介质的材料在空间按照一定的周期顺序排列所形成的有序结构电介质材料,它具有尺度为光波长量级的重复结构单元,通过对这些结构单元的合理设计,可以调控光子晶体的光学性质[3] 。光子晶体的主要特征就是在它的能带谱中存在光子导带和光子禁带,当光子在光子晶体内传输时,频率落在禁带范围内的光子将不能在光子晶体中传播,同时频率落在带隙内的原子的自发辐射也将会被抑制,而频率位于导带的光子则能在光子晶体里几乎无损地传播。光子带隙的宽度和位置与光子晶体的折射率、周期排列的结构尺寸及排列规则都有关系。但与电子相比,光子具有更多的信息容量、更高的效率、更快的响应速度以及更低的能量损耗[3] [4] 。
近年来,光子晶体不仅在传感器、光开关、医学领域取得了广泛的应用,也为化学及生物传感器领域提供了新的检测原理和手段[5] 。本文以光子晶体的基本禁带理论为基础,运用平面波展开法的Matlab编程程序语言模拟了介电常数不同的二维光子晶体结构的禁带特征。结合给定的数据阐述了禁带特性受光子晶体结构参数的影响,同时提出了光子晶体在浓度测量计方面的设计及其传感器领域内的应用。
2. 平面波展开法
在平面波展开法中,首先采用Bloch定理将介电常数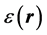 按Fourier级数展开,然后再以Maxwell方程组计算,从而求得光子晶体的能带结构。考虑光子晶体材料为各向同性,无源,非磁性,无吸收,则从Maxwell程组可以写成如下的本证方程[6]
按Fourier级数展开,然后再以Maxwell方程组计算,从而求得光子晶体的能带结构。考虑光子晶体材料为各向同性,无源,非磁性,无吸收,则从Maxwell程组可以写成如下的本证方程[6]
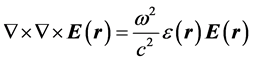 (1)
(1)
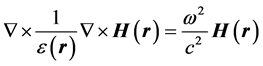 (2)
(2)
其中,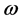 为频率,c为光速,
为频率,c为光速,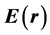 和
和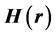 分别为电场和磁场强度,采用Bloch定理将介电常数
分别为电场和磁场强度,采用Bloch定理将介电常数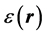 、电场和磁场强度按Fourier级数展开[7] :
、电场和磁场强度按Fourier级数展开[7] :
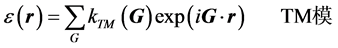 (3)
(3)
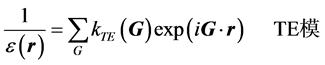 (4)
(4)
其中,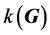 是周期分布的
是周期分布的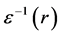 的Fourier系数。波矢
的Fourier系数。波矢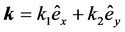 ,
,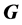 为晶格的二维倒格矢,可写作
为晶格的二维倒格矢,可写作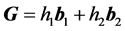 ,
,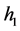 和
和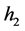 为整数,
为整数,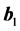 和
和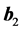 为二维光子晶体的倒格基矢。本文只分析在二维TE偏振,在TE模偏振下,磁场强度的Fourier级数展开式:
为二维光子晶体的倒格基矢。本文只分析在二维TE偏振,在TE模偏振下,磁场强度的Fourier级数展开式:
 (5)
(5)
式中,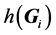 为Fourier系数。将式(5)代入式(2),并利用磁场的横向条件,波动方程可以被转换成下面的代数方程
为Fourier系数。将式(5)代入式(2),并利用磁场的横向条件,波动方程可以被转换成下面的代数方程
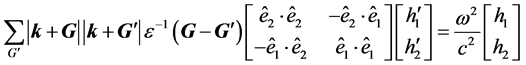 (6)
(6)
也可以写成式(7)的矩阵形式
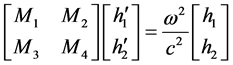 (7)
(7)
在二维情形下,如果矢量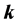 和
和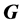 在x0y平面内,则
在x0y平面内,则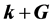 也在x0y平面内,因此,
也在x0y平面内,因此,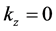 ,于是式(7)中的
,于是式(7)中的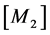 和
和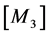 变为零矩阵,这时式(6)简化成以下形式
变为零矩阵,这时式(6)简化成以下形式
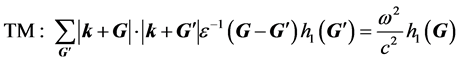 (8)
(8)
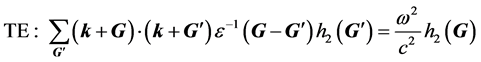 (9)
(9)
式(7)将电磁波在光子晶体中的传播问题转化为对无限多个倒格矢量的求和问题,本文中用有限个倒格矢量的求和法进行计算。由于每个原胞由介电常数分别为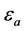 ,
,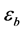 的两种材料组成,此时上述的式(4)中的系数可表示为
的两种材料组成,此时上述的式(4)中的系数可表示为
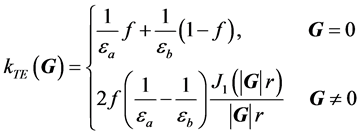 (10)
(10)
其中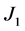 为一阶贝塞尔函数,
为一阶贝塞尔函数,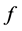 为填充因子(正方晶格
为填充因子(正方晶格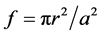 ,三角晶格
,三角晶格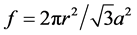 ),
),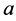 为晶格常数,
为晶格常数,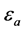 是空气孔的介电常数,
是空气孔的介电常数,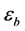 是背景材料的介电常数。将(10)式代入(9)式,即可求出H偏振的本征频率ω。
是背景材料的介电常数。将(10)式代入(9)式,即可求出H偏振的本征频率ω。
3. 光子晶体的结构
以半导体材硅(Si)为背景介质材料,采取在平面板上空气打孔方式产生光子晶体,待测溶液充入二维圆柱三角形晶格光子晶体中(如图1所示)。
由图可知,圆柱空气孔呈三角晶格排列,并且沿轴向无限伸展构成二维周期性阵列,即在Si(ε = 11.7)介质材料上钻孔,使空气孔(ε = 1)呈二维周期性排列。下面利用平面波展开法对它进行数值模拟计算。
4. 数值分析
本文中对三角晶格的空气孔结构光子晶体的TE模禁带特性来研究待测溶液禁带宽度和浓度之间的
变化关系。如图1所示的晶体结构中,注入圆柱形空气孔的氯化钾[8] 介电常数分别为ea = 1.804,1.824,1.833,1.846,1.873,背景材料硅(Si)的介电常数为eb = 11.7,空气孔的半径为R/a = 0.4 μm,晶格常数为1 μm,模数为n = 6,氯化钾水溶液的质量百分比浓度变化范围限定为2.5%,5%,7%,10%,20%(单位:gm/ml)。图中纵坐标采用标度化的无量纲频率ωa/2πc(a/λ),而横坐标采用标度化的Bloch波矢k,经过多次模拟可以发现,由于在TE模上出现较大的隙[9] [10] ,因此本文只限TE模。
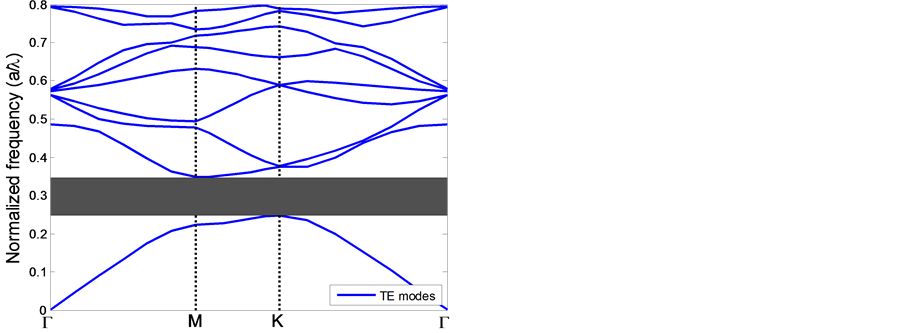
图2(a)和图2(b)表示氯化钾的质量百分比浓度为2.5%和20%的带隙,从图2(a)中可以看出,二维三角晶格晶体的TE模中只有1个能隙,即:Gap = 0.248~0.350。相应带宽为0.339(Δ = 33.9%),而2(b)中也出现与图2(a)相似的较大带隙,即:Gap = 0.248~0.345,相应带宽为0.339(Δ = 32.8%)。
由不同百分浓度和介电常数情形下,对三角晶格光子禁带进行数值模拟计算得到了表1所示的禁带宽度。见表1从表可以看出,当注入圆柱空气孔的质量百分浓度由2.5%到20%,而介电常数1.804到1.873变化时,以Si背景的光子晶体都存在较大的光子带隙。计算发现当空气孔的质量百分浓度和介电常数变增大时,三角晶格光子晶体TE模的最大带隙宽度逐渐减少。
将表1中的氯化钾溶液浓度、介电常数和相应带隙宽度的数据进行拟合,得如图3和图4所示的拟合线。由图3可知,当氯化钾溶液的百分浓度较低时,介电常数处于较低点,曲线总体趋势来看,介电常数与溶液百分浓度显著保持线性关系。
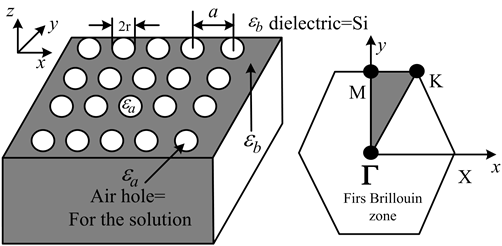
Figure 1. Two dimensional triangular photonic crystal and first Brillouin zone
图1. 二维三角晶格光子晶体结构和第一布里渊区
Triangular Lattice (εa = 1.804, εb = 11.7, R = 0.4) Triangular Lattice (εa = 1.873, εb = 11.7, R = 0.4)
 (a)
(a)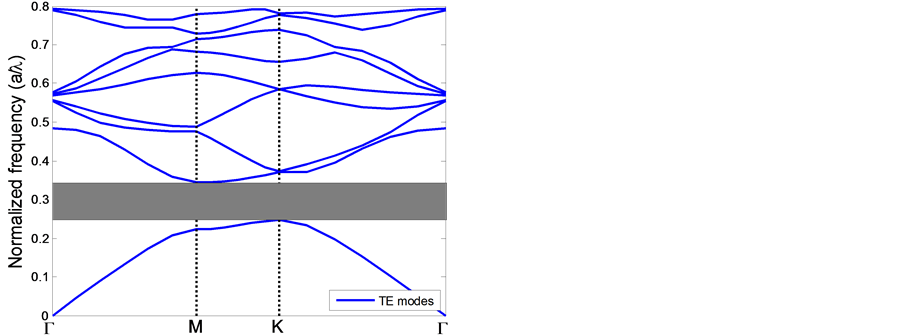 (b)
(b)
Figure 2. TE (blue lines) band structure for (a) a triangular lattice of Si (eb = 11.7) rods in KCl (ea = 1.804) and (b) a triangular lattice of Si (eb = 11.7) rods in KCl (ea = 1.873)
图2. 二维三角介质光子晶体的TE模(蓝线)能带结构。(a) 背景硅介质(eb = 11.7)和待测溶液KCl(ea = 1.804);(b) 背景硅介质(eb = 11.7)和待测溶液KCl(ea = 1.873)

Table 1. The dielectric constant of the KCl solution of percent concentration and band structure (273.1 K) [8]
表1. 不同百分浓度的氯化钾–水溶液的介电常数和带隙(273.1 K) [8]
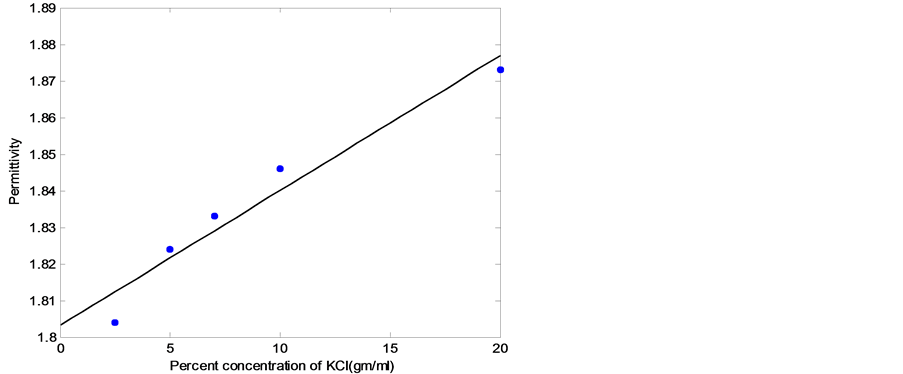
Figure 3. Dependence of percent concentration KCl solution and permittivity
图3. KCl溶液百分浓度与其介电常数之间的变化关系
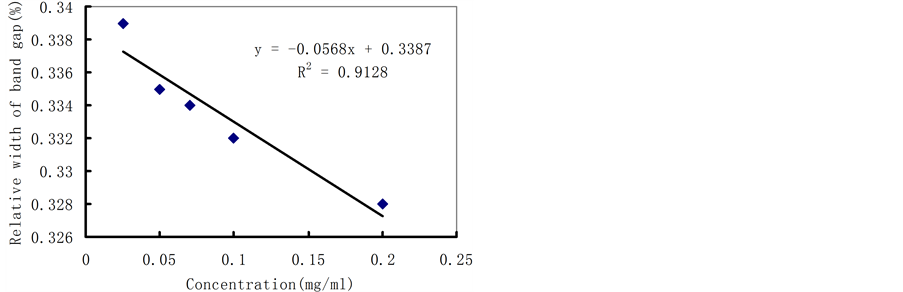
Figure 4. Dependence of band gap width as a function of percent concentration of KCl solution
图4. 禁带宽度随KCl溶液百分浓度的变化关系
由图4可知,在室温下,氯化钾溶液的百分浓度与其光子带隙约呈现线性关系。
溶液的百分浓度增大时,其对应的光子带隙最大宽度随之变小,且呈一定的比例关系。
图4可知,KCl溶液百分浓度与溶液禁带宽度之间的线性关系为:
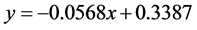 (11)
(11)
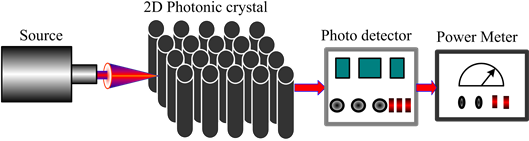
Figure 5. Experimental facility for the measurement of KCl percent concentration
图5. 测量KCl溶液百分浓度的实验装置
式中x为273.1 K的KCl溶液浓度,y为禁带宽度,线性拟合度R2 = 0.9128。而KCl溶液中的百分含量由2.5%增大到20%时,在室温273.1 K下的KCl溶液的禁带宽度随溶液浓度的增加而减少。
本研究的设计中二维三角晶格光子晶体的空气孔内填待测溶液以后,将光子晶体的两侧用两个玻璃片封住(如图5所示),然后用一定波长的纳光灯照射光子晶体,光子晶体在吸收光后其晶体带隙结构会发生变化,从而会引起透射率的改变,这便是光子晶体传感器的百分浓度检测原理。通过测量透射率的变化或者带隙变化关系来测定溶液的百分浓度。
5. 结论
用平面波展开法,对二维光子晶体的能带结构和传输特性进行了理论分析。以Si介质为本底材料,以禁带宽度较大的三角晶格光子晶体TE模的禁带模型为研究对象,计算了不同百分浓度情况下光子晶体带隙宽度的变化状况。结果表明TE模式下的光子带隙随溶液百分浓度的不同而发生变化,也就是光子带隙随溶液百分浓度的增加而变小。这种方法展示了利用二维光子晶体来测量溶液浓度的新型方法。
项目基金
国家自然科学基金(11164030,11465019)的资助。