1. 引言
近些年来,随着机器情感研究的不断深入和家用智能机器人的日益普及,非人形机器人的情感交互问题成为新的研究热点。旋翼空中机器人以其多自由度和强机动性的特点,逐渐受到研究者的青睐。针对空中机器人基于运动轨迹的情感表达问题,文献[1] 提出了一种基于LMA的情感表达轨迹链自动设计方法。通过建立轨迹链参数与情感表达的关系模型,设计轨迹链-情感标准集,并在此基础上提出了一种基于LMA理论的机器人运动轨迹链情感表达模型。该方法为机器人完全自主地通过运动轨迹链表达情感奠定了基础。
然而,单一空中机器人的情感表达行为,受到机体本身自由度的限制,只能进行有限的动作,限制了行为的多样性,影响情感表达的效果。多空中机器人编队通过协同的动作和队形的变化来表现不同的情感,可以丰富情感表达的行为,使情感表达更为充分。
多机器人情感表达问题在地面机器人平台上已经进行了一些研究[2] 。与地面机器人编队相比,由于空中机器人的动力学特性,其协同控制问题更为复杂。针对这一问题,宾夕法尼亚大学GRASP实验室的V. Kumar等人提出了一种对四旋翼无人机机队队形进行控制的方法,该方法中机器人在根据指令变换队形时跟随一个指定的群体轨迹[3] -[5] 。瑞士苏黎世联邦理工大学的D’Andrea等人开发了一个用两架四旋翼无人机进行有节奏飞行的平台。结果证明当将摆动运动与音乐节拍准确定时时,声音与运动同步是可行的[6] 。但目前的研究只停留在飞行器根据音乐节拍和强度进行编排和同步,并不能有效地表达音乐中所蕴含的情感。
在这些研究的基础上,针对多空中机器人情感表达问题,在单机器人情感表达行为设计方法中加入了队形变化的因素,并采用了基于音乐节拍的多空中机器人同步方法,为多空中机器人具有情感表达功能的协同舞蹈表演提供了基础。
2. 多空中机器人情感表达行为设计
文献[1] 中基于PAD情感空间,研究了四种基本情感在PAD空间中的极性以及运动轨迹的效果因子的极性,如表1所示。
对多空中机器人编队,影响情感表达的因素除效果因子外,还包括编队队形的变化。以一个由四架空中机器人组成的编队为例,典型的队形变化如图1所示。

Table 1. The polarity in the PAD space and the value of effect factors for 4 basic moods
表1. 四种基本情感在PAD空间及效果因子的极性
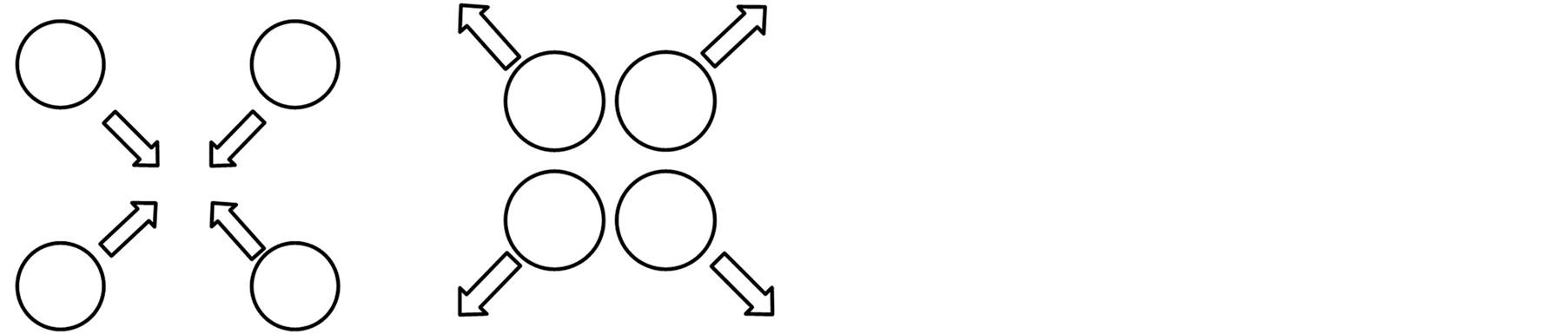
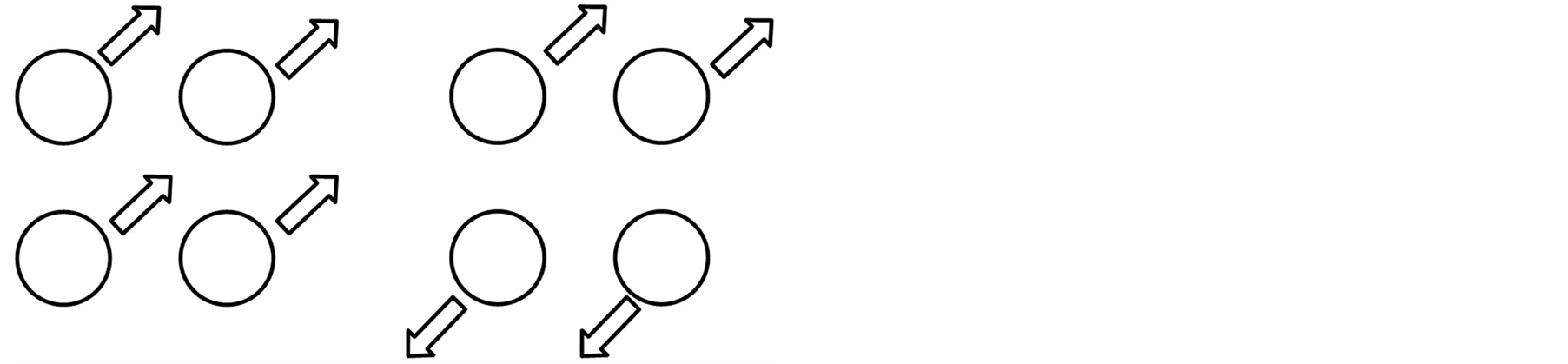
Figure 1. The classical formation of multiple aerial robots
图1. 多空中机器人编队典型构型
根据[7] 中的研究,编队在空间中分布的改变与PAD空间中的激活度分量相关。空间变小的运动对应激活度较低,反之空间扩大的运动对应激活度较高。因此队形的收缩使编队在空间中的分布变得集中,给人以内向化的感觉,对应PAD空间中激活度减小。适于表现悲伤、恐惧、忧郁的情感。同理,队形的扩张使编队在空间中分布范围变大,给人以外向化的感觉,对应PAD空间中的激活度增大。当速度适中、轨迹较平滑时,适于表现快乐的情感;当速度极快、轨迹较尖锐时,适于表现愤怒的情感。
而队形的一致性与PAD空间中的愉悦度相关。编队中每个个体的运动方式的一致性越高,对应的愉悦度越高。因此,所有机器人保持一个固定队形的运动,适于表现愉快的情感,而杂乱无章的运动,适于表现愤怒或悲伤的情感。特别地,进行镜像运动的机器人,虽然它们的运动并非完全一致,但其运动模式是一致的,而仅在运动方向上相反,这样的运动相对一致性运动更为活泼,适于表现欢快活泼的场景。队形与情感表达的关系如表2所示。
3. 多空中机器人同步性研究
在多机器人舞蹈表演中,各个机器人动作的协调和同步是表演效果的关键。为了实现各个机器人间动作的同步,采用了一种基于音乐节拍的同步方法,利用锁相环的概念设计同步控制器,通过相位比较器和修正算法修正音乐和实际运动之间的相位误差。
由于摆动动作具有周期性,因此以该运动为例,研究运动动作与节拍同步的问题。空中机器人进行摆动运动时,在节拍点达到轨迹的最高点。首先对音乐进行预处理,将获得的节拍点信息变换成一组周期信号,作为运动生成的依据。控制系统如图2所示。若音乐参考信号和机器人实际运动同相位,即可得到与旋律同步的行为。
将音乐信号进行特征提取后得到相位参考信号,将其与机器人运动的实际状态进行比较得到相位差,根据相位差进行相位修正,使机器人的动作与音乐节拍相一致。
3.1. 系统描述
为了能够使存在的相位误差可视化并成功锁相,选择了简单的摆动运动作为参考轨迹。横向运动的振幅和频率随相应的音乐旋律和节拍间隔调整。
分析一段音乐可得到目标节拍T和振幅Ad。这些值确定了参考轨迹。相应的目标轨迹是一个在xz平面内的正弦摆动运动:
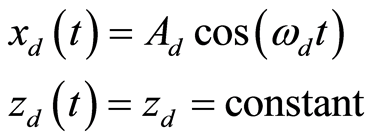 (1)
(1)
其中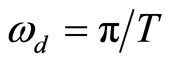 。节拍出现在轨迹的峰值处,即每个周期两次。
。节拍出现在轨迹的峰值处,即每个周期两次。
(1)式中的摆动运动定义在xz平面内,因此进出平面的运动被分离且其余的自由度分别稳定。约束系统的动力学方程由下式给出:
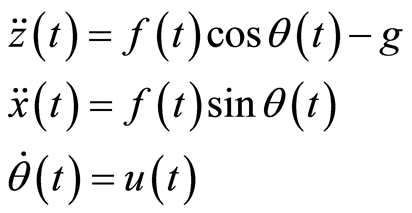 (2)
(2)
其中g为重力加速度,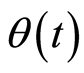 为俯仰角。系统输入为标准化升力
为俯仰角。系统输入为标准化升力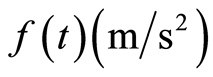 和俯仰角速度
和俯仰角速度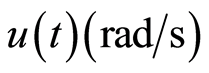 。
。
3.2. 控制器设计
使系统稳定在高度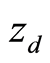 的升力输入:
的升力输入:
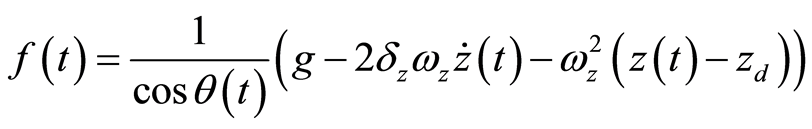 (3)
(3)

Table 2. The features of the trajectory chain and formation for different moods
表2. 不同情感的轨迹链与队形特点
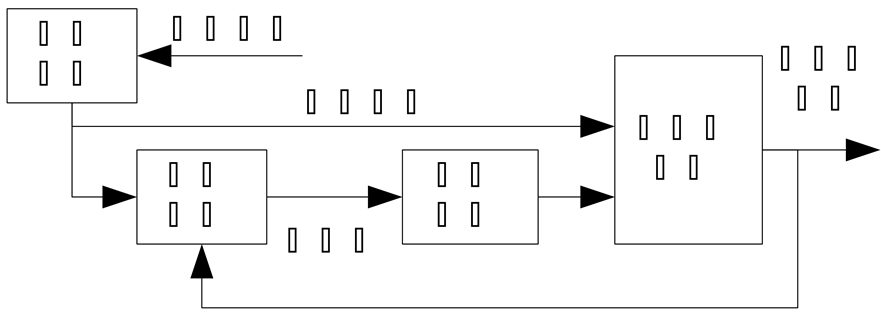
Figure 2. The schematic of the control system
图2. 控制系统示意图
闭环动力学由下式给出
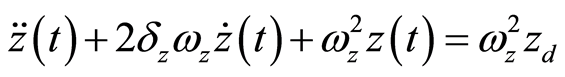 (4)
(4)
阻尼比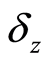 在0.7到1之间。需要设计的参数就只有自然频率
在0.7到1之间。需要设计的参数就只有自然频率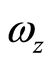 。
。
3.3. 轨迹跟踪
假定高度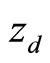 为常量,x轴方向的动力学方程(2)式化简为:
为常量,x轴方向的动力学方程(2)式化简为:
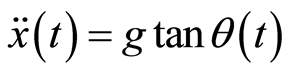
由于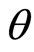 很小,可近似得到
很小,可近似得到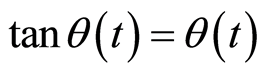
得到近似线性化模型:
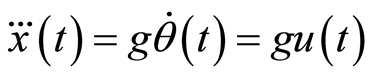 (5)
(5)
其中,摆动运动的输入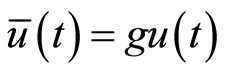 包括前馈分量:
包括前馈分量:
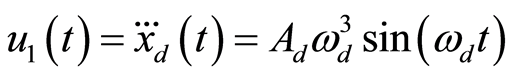
和修正误差的反馈项:
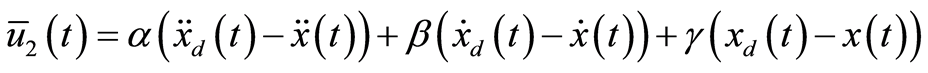
其中控制参数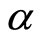 、
、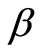 和
和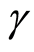 定义为:
定义为:
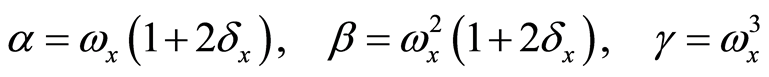 (6)
(6)
分别作用于加速度、速度和位置误差。选择(6)中的参数,闭环系统的特征多项式为:
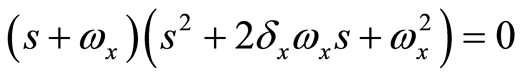 (7)
(7)
最后,系统输入为:
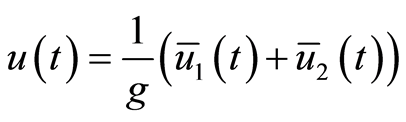 (8)
(8)
3.4. 同步算法
定义参考信号
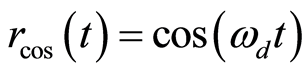 (9)
(9)
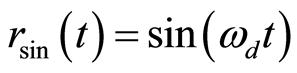 (10)
(10)
近似线性化系统的响应为周期信号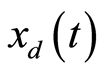
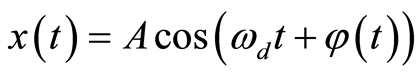 (11)
(11)
将(11)式分别与(9)和(10)式相乘得:
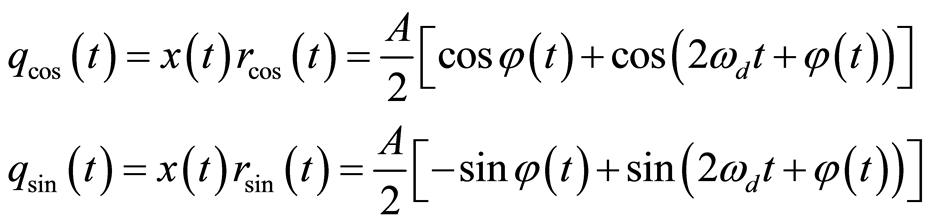 (12)
(12)
在一个周期 上对这些信号积分,并假设相位偏移在该时间段上为常量:
上对这些信号积分,并假设相位偏移在该时间段上为常量:
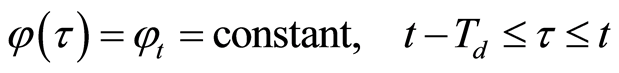
得到:
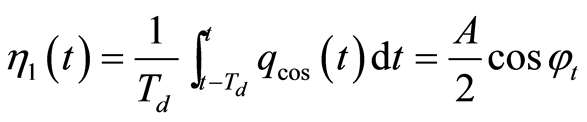
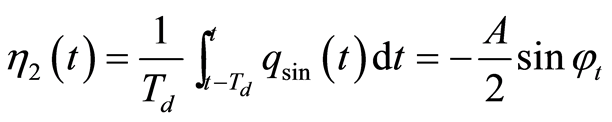
相位偏移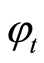 可由下式得到:
可由下式得到:
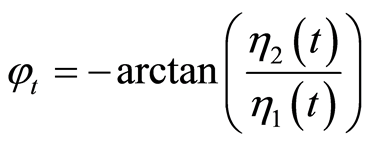
相位误差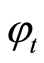 通过根据PLL原理设计的反馈环节进行修正。(1)中的参考信号
通过根据PLL原理设计的反馈环节进行修正。(1)中的参考信号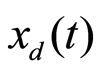 由修正项
由修正项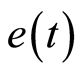 替换:
替换:
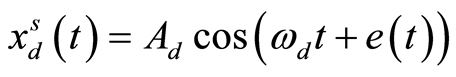 (13)
(13)
定义为:
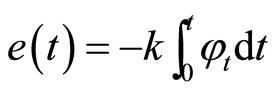 (14)
(14)
类似的, 的各阶导数的相位修正量为e(t)。在控制方程(5)中将参考信号xd(t)及其各阶导数替换为修正值,
的各阶导数的相位修正量为e(t)。在控制方程(5)中将参考信号xd(t)及其各阶导数替换为修正值,
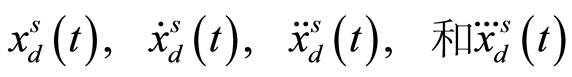
得到新的输入u(t),参见(4),即修正相位误差。同时考虑反馈增益项e(t),即可得到准确和鲁棒的锁相器。通过调节增益系数k使其达到收敛。
4. 实验结果
4.1. 实验环境
实验平台为基于四旋翼飞机的情感表达系统,系统由计算机、路由器,以及两架如图3所示的空中机器人组成。
考虑到系统中智能体的数量有限,且对同步性要求较高,故采用集中式体系结构。

Figure 3. Aerial robot platform for emotion expression
图3. 情感表达空中机器人平台
4.2. 多空中机器人基于音乐节拍的同步实验
利用MATLAB对3.4中的同步算法进行了仿真。保持y和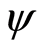 通道控制量为0,z通道控制量为恒定值1,即y方向位置不变,高度不变,偏航角不变,只改变x通道的控制量,使机器人在x方向上依照参考信号进行摆动。参考信号频率
通道控制量为0,z通道控制量为恒定值1,即y方向位置不变,高度不变,偏航角不变,只改变x通道的控制量,使机器人在x方向上依照参考信号进行摆动。参考信号频率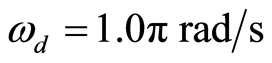 ,振幅Ad = 0.5 m。图4表示了AR在三种情形下的响应:1) 无相位修正;即(13)式中k = 0;2) 有相位误差修正,k = 0.28;3) 基于预先确定值的前馈相位和振幅误差修正。
,振幅Ad = 0.5 m。图4表示了AR在三种情形下的响应:1) 无相位修正;即(13)式中k = 0;2) 有相位误差修正,k = 0.28;3) 基于预先确定值的前馈相位和振幅误差修正。
使用两架空中机器人进行了同步控制的实验,实验平台选用两架AR.Drone 2.0四旋翼飞行器,通过一台路由器与主控计算机进行通讯。由于机体本身质量较轻,对气流干扰较明显,在实验过程中受风向和风力影响较为明显。但由于飞机本身采用光流法进行位置补偿,需选择有一定照度的环境,因此,综合考虑各方面要求,实验选择户外进行。分别进行了同步起飞、完成指定动作和降落的实验。图5(a)中展示了同步起飞后的效果;图5(b)中展示了同步完成指定动作的效果。
实验表明,采用3.4节中的算法,可以实现两空中机器人的同步运动,误差小于0.1秒,满足多机协同舞蹈的需要。
5. 结论
本文针对多空中机器人情感表达中的关键问题,进行了如下研究:
1) 针对多空中机器人的情感表达问题,在情感表达中融入了队形因素,研究了基于队形变化的情感表达策略。采用了基于向量图的多空中机器人队形保持和变换算法,每个机器人基于其临近机器人的本地信息独立地规划其路径,实现多空中机器人队形控制。



Figure 4. Experiment result
图4. 实验结果


Figure 5. Synchronous control experiment
图5. 同步控制实验
2) 针对多空中机器人舞蹈的同步性问题,提出了基于音乐特征的同步方法。通过对音乐信号的处理,提取出音乐特征,利用节拍等信息实现多个空中机器人的同步。以摆动运动为例,研究了基于音乐节拍的同步方法。
搭建了多空中机器人舞蹈实验平台,通过仿真实验和实际实验验证了以上方法的有效性。