1. 引言
时变时滞中立系统是指中立时滞和状态时变时滞均为时变的中立型系统.时变时滞中立系统已有许多深刻的研究结果,例如文献[1] -[2] 用莱布尼茨公式和自由权矩阵方法研究时变时滞中立系统的稳定性。具有非线性扰动的时变时滞中立型系统引起了许多研究者的兴趣,例如文献[3] 研究具有非线性扰动的指数稳定性,文献[4] 研究具有非线性扰动的中立型系统的鲁棒稳定性。此外,文献[5] -[7] 所研究的系统不仅具有非线性扰动,而且有不同的中立时滞和时变时滞。本文研究一类更一般的具有非线性扰动的时变时滞中立型系统,对此系统进行稳定性分析,并给出渐近稳定的充分条件。
本文考虑如下具有时变时滞中立型系统:
 (1.1)
(1.1)
其中 表示系统的状态向量,
表示系统的状态向量, ,
, 是常数矩阵,
是常数矩阵,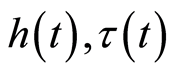 分别是中立时滞和时变时滞,满足:
分别是中立时滞和时变时滞,满足:
 (1.2)
(1.2)
这里 都是正常数,
都是正常数, 是在
是在 上连续的初始函数。并且
上连续的初始函数。并且
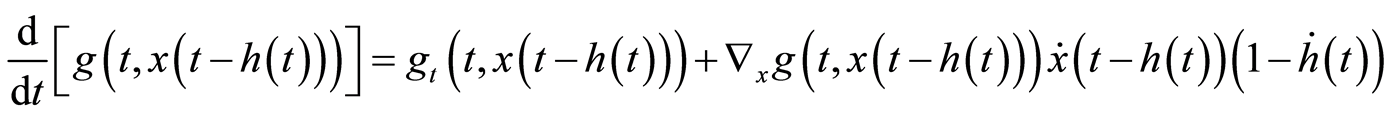
记 ,
, ,其中非线性函数
,其中非线性函数
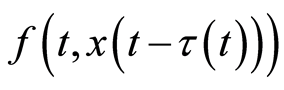 ,
,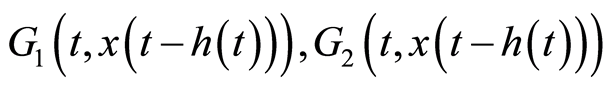
满足: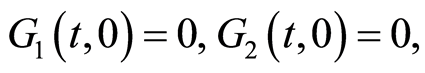
 及
及
 (1.3)
(1.3)
其中 是给定的常数。
是给定的常数。
2. 具有非线性扰动的时变时滞中立系统的稳定性分析
系统(1.1)改写为:
 (2.1)
(2.1)
为了得到系统(2.1)的稳定性条件,我们需要下面的引理。
引理2.1 [5] 对于任意常矩阵 ,常数
,常数 有
有

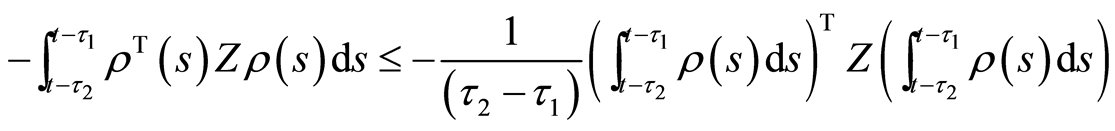 .
.
引理2.2(Schur补)[8] 给定适当维数的常矩阵 ,
, ,
, ,那么
,那么
 成立,当且仅当
成立,当且仅当
 或者
或者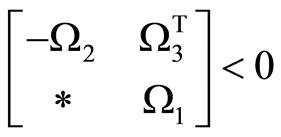 。
。
引理2.3[9] 给定适当维数的矩阵 ,那么对于所有满足
,那么对于所有满足 的
的 ,不等式
,不等式 成立的充分必要条件是存在一个常数
成立的充分必要条件是存在一个常数 使得
使得 。
。
根据Lyapunov理论,对于系统(2.1)的Lyapunov-Krasovkii泛函 ,如果
,如果 ,那么系统(2.1)是渐近稳定的。从而有如下结果:
,那么系统(2.1)是渐近稳定的。从而有如下结果:
定理2.1. 对于给定的常数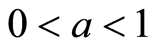
 满足条件(1.2)、(1.3),且存在线性矩阵不等式:
满足条件(1.2)、(1.3),且存在线性矩阵不等式:
 ,
,
 ,
, ,
,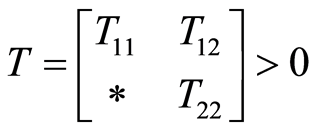 ,
,
 ,
, ,
, ,
,
和存在常数: ,
, 使得下列线性矩阵不等式成立:
使得下列线性矩阵不等式成立:
 (2.2)
(2.2)
其中
 ,
,
 ,
,
 ,
,  ,
,  ,
, 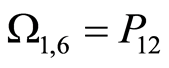 ,
,  ,
,  ,
,  ,
,
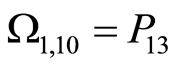 ,
,  ,
,  ,
,  ,
,
 ,
, 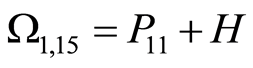 ,
,  ,
,
 ,
,
 ,
,  ,
,  ,
,  ,
, 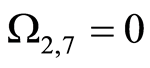
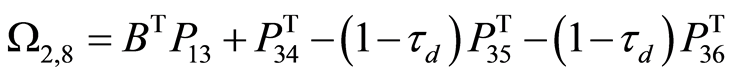 ,
,  ,
,  ,
,  ,
,
 ,
,
 ,
,
 ,
,  ,
,  ,
,
 ,
,  ,
,
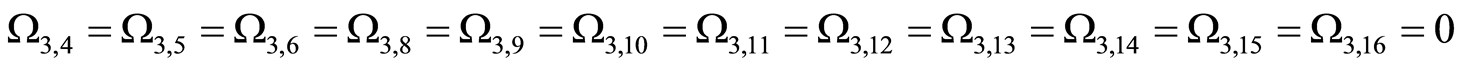
 ,
, 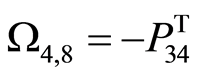 ,
,  ,
,
 ,
,  ,
,  ,
,  ,
,
 ,
,  ,
,  ,
,
 ,
,  ,
,  ,
,  ,
,
 ,
,  ,
,  ,
,  ,
,
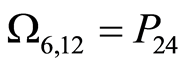 ,
, 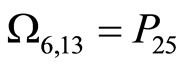 ,
,  ,
,  ,
,  ,
,
 ,
,  ,
,
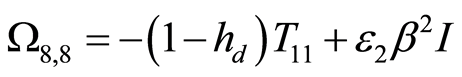 ,
,  ,
,  ,
,  ,
,
 ,
,  ,
,  ,
,
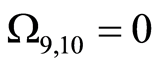 ,
,  ,
,  ,
,
 ,
, 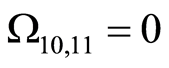 ,
,  ,
,  ,
,  ,
,  ,
,
 ,
,  ,
, ,
,
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,
 ,
,  ,
,
 ,
,
 ,
,
 ,
,  ,
, 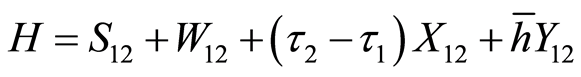 ,
,
 ,
, .
.
则系统(2.1)是渐近稳定的。
证明:选取恰当的Lyapunov-Krasovkii泛函: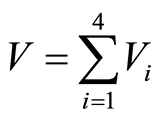
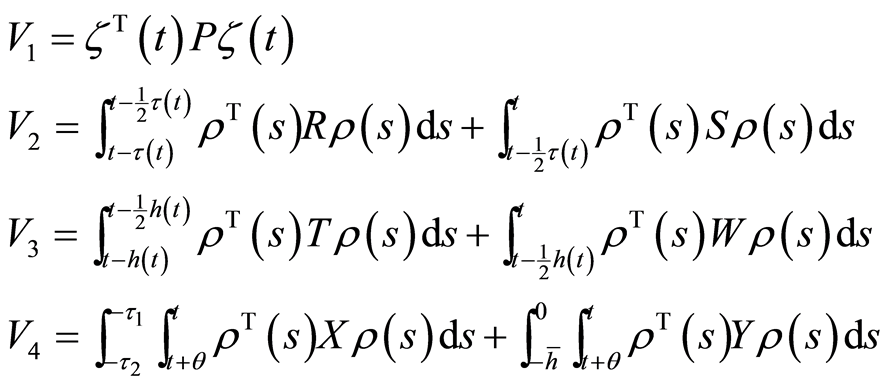 (2.3)
(2.3)
其中
 ,
,
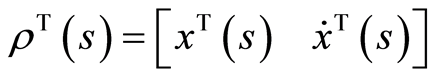
对 关于
关于 沿着系统(2.1)求导:
沿着系统(2.1)求导:

 (2.4)
(2.4)
其中, 中各项都是正定的,且
中各项都是正定的,且 。
。
 (2.5)
(2.5) (2.6)
(2.6)
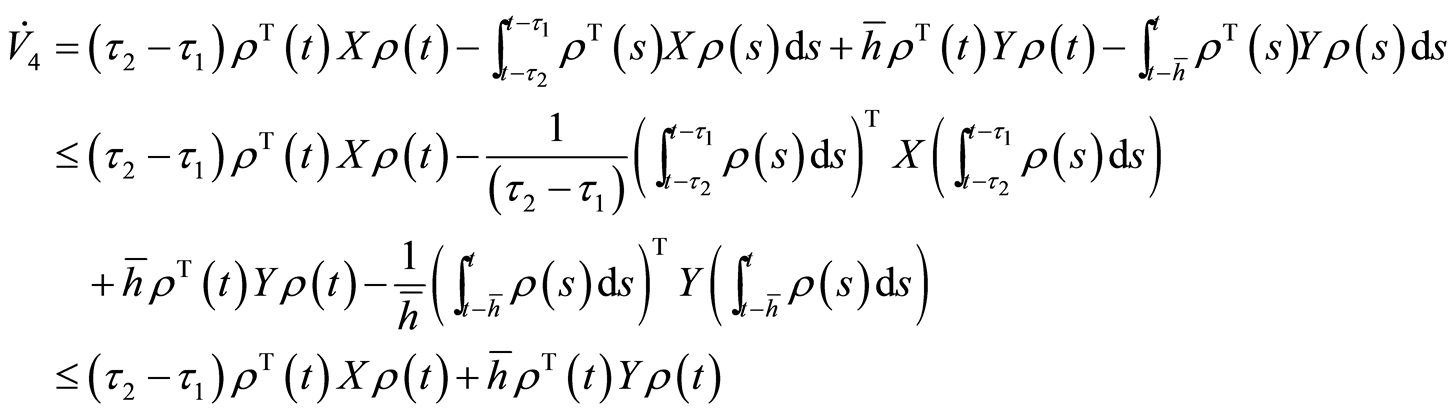 (2.7)
(2.7)
 (2.8)
(2.8)
由(1.3)可得,对于任意常数 有
有
 (2.9)
(2.9)
然后结合方程(2.8)~(2.9)和引理2.1可知:
 (2.10)
(2.10)
其中 ,
, ,
,

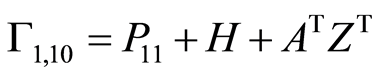 ,
,  ,
,
 ,
,
 ,
,
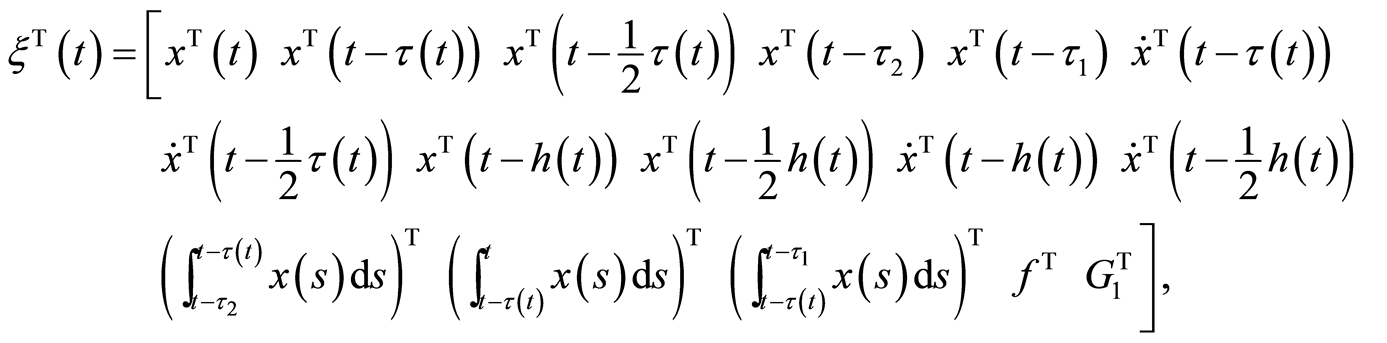
结合引理2.3,存在常数 ,使得
,使得
 (2.11)
(2.11)
由(1.3),引理2.2和引理2.3得(2.11)等价于(2.2),即 。
。
因此,带有非线性扰动的时变时滞中立型系统(2.1)是渐近稳定的,证毕。
3. 注记
本文对于构造的Lyapunov-Krasovskii泛函做出了改进,即,把中立时滞和时变时滞分成两段
 ,
,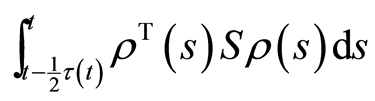 ,
,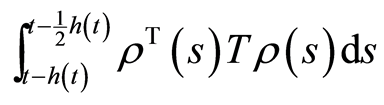 ,
,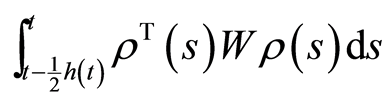 ,因此Lyapunov
,因此Lyapunov
泛函的时域被划分得更精细。同时,本文用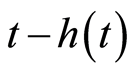 来代替积分下限
来代替积分下限 ,这样处理有利于降低系统的保守性。
,这样处理有利于降低系统的保守性。
对于Lyapunov泛函的导数,产生了非对称项如 ,并不能直接使用LMI处理问题。因此,对非对称项进行有效的放缩以保证系统的可控制性,并且尽可能降低系统的保守性。应用引理2.3,非对称项可被对称项有效控制,从而使得Lyapunov泛函的导数被约束在一个可控制的线性矩阵不等式中,最后得到判定系统稳定性的充分条件。
,并不能直接使用LMI处理问题。因此,对非对称项进行有效的放缩以保证系统的可控制性,并且尽可能降低系统的保守性。应用引理2.3,非对称项可被对称项有效控制,从而使得Lyapunov泛函的导数被约束在一个可控制的线性矩阵不等式中,最后得到判定系统稳定性的充分条件。