1. 引言
三电平逆变器[1] 可以在不降低功率和电压等级的情况下使得开关管承受的最大电压降低一半,同时使得开关管频率降低一半,大大降低了对开关管的要求,降低了成本。同时三电平逆变器的输出谐波大大降低,输出波形质量得到提高。由于以上优点三电平逆变器在高压大功率的逆变应用场合得到了广泛应用[2] 。本文针对三电平SVPWM控制算法[3] 进行了研究,详细叙述了三电平SVPWM的DSP实现方法。
2. 二极管钳位式三电平逆变器的拓扑
二极管钳位式三电平逆变器的拓扑[4] 如图1所示,在平衡状态直流母线上的两个电容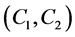 的电压等于直流母线电压的一半,桥臂上的钳位二极管
的电压等于直流母线电压的一半,桥臂上的钳位二极管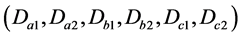 导通时,相应点的电位会被钳位到直流母线电容中点电位。以A相桥臂为例,当
导通时,相应点的电位会被钳位到直流母线电容中点电位。以A相桥臂为例,当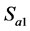 、
、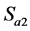 导通时,桥臂中点输出
导通时,桥臂中点输出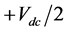 电位(用P表示),当
电位(用P表示),当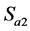 、
、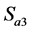 导通时,桥臂中点输出0电位(用O表示),当
导通时,桥臂中点输出0电位(用O表示),当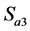 、
、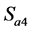 导通时,桥臂中点输出
导通时,桥臂中点输出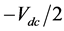 电位(用N表示)。其中点输出电位与开关管的关系[5] 如表1所示。
电位(用N表示)。其中点输出电位与开关管的关系[5] 如表1所示。
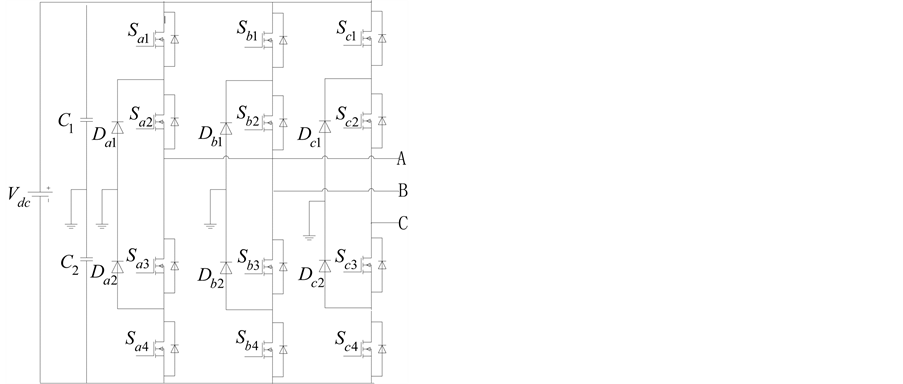
Figure 1. Diagram of NPC
图1. 二极管钳位式三电平逆变器

Table 1. The relationship between output voltage and the switch
表1. 输出电位与开关管的关系
通过表1可以看出,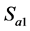 与
与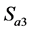 互补导通,
互补导通,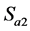 与
与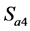 互补导通,而且当
互补导通,而且当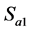 开通时(输出
开通时(输出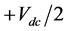 )
)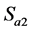 一定开通,当
一定开通,当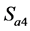 开通时(输出
开通时(输出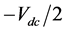 )
)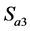 一定开通。这些开关管的逻辑关系在三电平SVPWM的实现中可以简化控制。
一定开通。这些开关管的逻辑关系在三电平SVPWM的实现中可以简化控制。
3. 三电平逆变器的矢量空间
三电平逆变器每个桥臂可以输出三种电平[6] ,所以ABC三相输出电平的组合一共有33 = 27个,因此共有27个开关矢量。这27个开关矢量可以分为长矢量、中矢量、小矢量和零矢量四类,分类结果如表2所示。其矢量空间如图2所示。
4. 三电平逆变器扇区判断方法
为了能够利用三电平的空间矢量[7] 合成出需要的参考矢量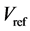 ,需要判断利用那三个矢量来合成
,需要判断利用那三个矢量来合成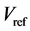 ,因此需要对矢量空间进行扇区划分,并判断
,因此需要对矢量空间进行扇区划分,并判断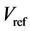 落在哪个扇区。
落在哪个扇区。

Table 2. Classify of three-level inverter
表2. 三电平逆变器矢量分类
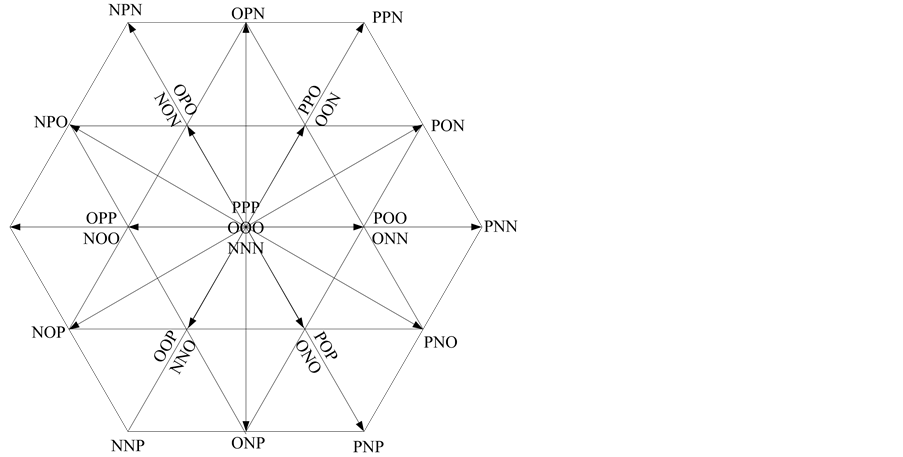
Figure 2. The space vector of three-level inverter
图2. 三电平逆变器的空间矢量
4.1. 传统的扇区判断方法
如图3所示为传统的扇区划分方法,6个长矢量将六边形划分为6个大三角形,每个大三角形又可以划分为4个小三角形。这种划分方法思路清晰,但是由于在不同的大三角形扇区中小三角形区域的判断方法不同,而且其矢量作用时间的计算也不相同,因此需要存储大量的数表,造成DSP资源的浪费,为此人们又提出了一种简化的三电平扇区判断方法。
4.2. 简化三电平扇区判断方法
如图4所示,分别以6小矢量的末端作为中心,将大六边形划分为6个小六边形,相邻两个小六边形有两个三角形重合,小六边形的编号N = 1, 2, 3, 4, 5, 6。小六边形的判断方法为:
参考电压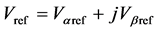 ,并令:
,并令:
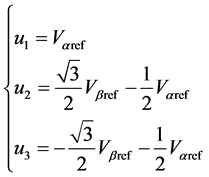 (1)
(1)
当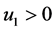 ,则
,则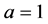 ,否则
,否则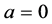 ;当
;当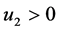 ,则
,则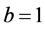 ,否则
,否则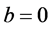 ;当
;当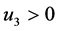 ,则
,则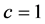 ,否则
,否则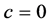 。令
。令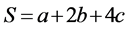 ,则
,则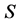 与小六边形编号N的关系如表3所示。
与小六边形编号N的关系如表3所示。
判断出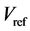 落在哪个小六边形后,还要判断
落在哪个小六边形后,还要判断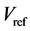 落在该小六边形的哪个三角形内,以N = 1小六边形为例,如图5所示。
落在该小六边形的哪个三角形内,以N = 1小六边形为例,如图5所示。
将原来大六边形的矢量空间的原点按照小矢量(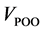 或
或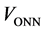 )移动到小六边形的中心,原来的大六边形的矢量和参考矢量都减去小矢量可以得到图5右边的矢量空间图,定义该小六边形的基矢量
)移动到小六边形的中心,原来的大六边形的矢量和参考矢量都减去小矢量可以得到图5右边的矢量空间图,定义该小六边形的基矢量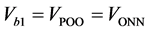 ,则:
,则: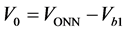 ,
,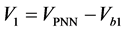 ,
,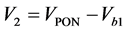 ,
,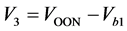 ,
,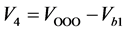 ,
,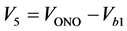 ,
,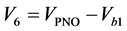 ,
,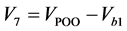 ,其矢量的选择要保证每次切换时发生动作的开关管数量只有两个,比如1区的矢量作用顺序为
,其矢量的选择要保证每次切换时发生动作的开关管数量只有两个,比如1区的矢量作用顺序为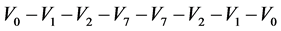 ,图中箭头表示前一半矢量的作用顺序,后一半矢量作用顺序与箭头方向相反。由此可以将三电平的矢量空间转化为6个两电平的矢量空间。
,图中箭头表示前一半矢量的作用顺序,后一半矢量作用顺序与箭头方向相反。由此可以将三电平的矢量空间转化为6个两电平的矢量空间。
4.3. 两电平矢量空间扇区判断
转化为两电平矢量空间的参考电压矢量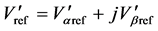 ,并令:
,并令:
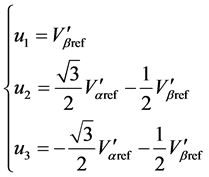 (2)
(2)
当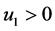 ,则
,则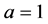 ,否则
,否则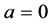 ;当
;当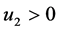 ,则
,则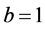 ,否则
,否则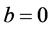 ;当
;当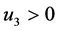 ,则
,则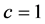 ,否则
,否则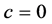 。
。
令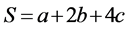 ,则S与小三角形编号M的关系如表4所示。
,则S与小三角形编号M的关系如表4所示。
4.4. 矢量作用时间的计算
由于矢量的作用顺序前后是对称的,所以只计算前半部分的矢量作用时间,以N = 1,M = 1扇区为
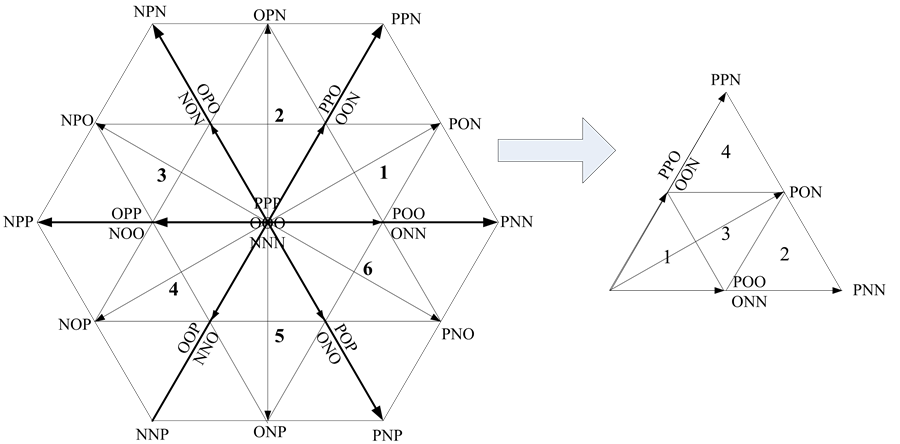
Figure 3. The traditional method of section judgment
图3. 传统的扇区判断方法
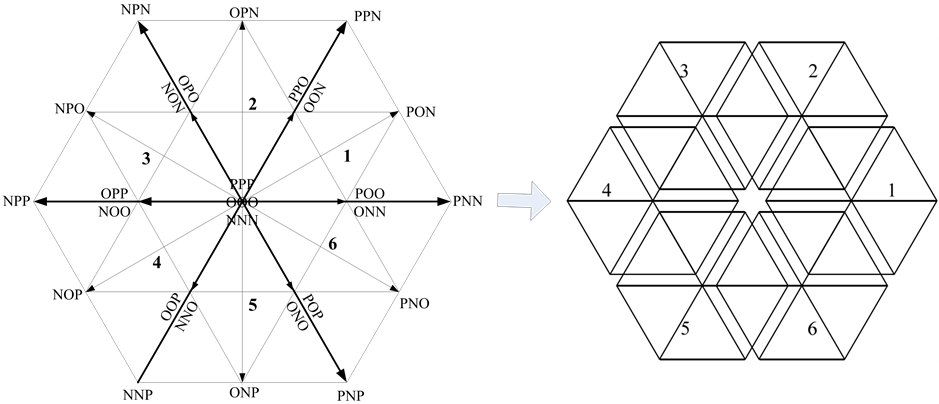
Figure 4. The simplified method of section division
图4. 简化扇区划分方法
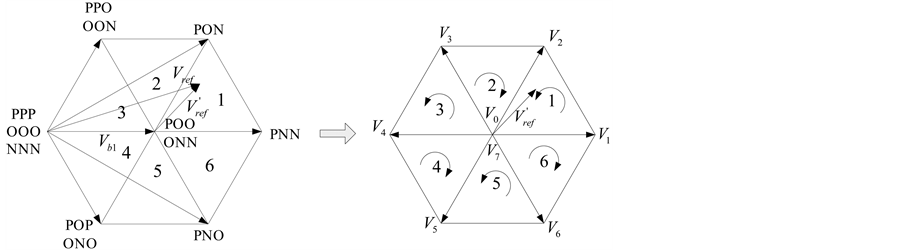
Figure 5. The space vector of No. 1 hexagon
图5. N = 1的小六边形矢量空间

Table 3. The relationship between S & N
表3. S与N的关系

Table 4. The relationship between S & M
表4. S与M的关系
例,如图5所示,该扇区内的矢量为:
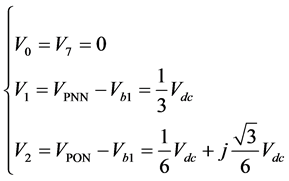 (3)
(3)
设开关周期为Ts,在前半个周期内,零矢量作用的时间为t0,第一个非零矢量作用的时间为t1,第二个非零矢量作用的时间为t2,由伏秒平衡得:
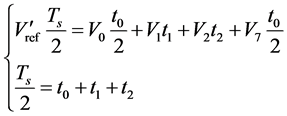 (4)
(4)
经过整理后可得:
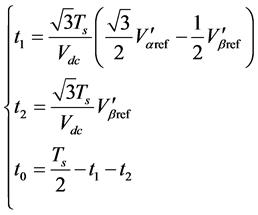 (5)
(5)
同理可以推出其余5个扇区内矢量的作用时间如表5所示。
其中:
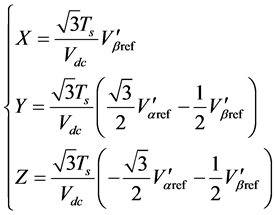 (6)
(6)
4.5. PWM波的产生
利用DSP28335的ePWM [8] 模块可以产生PWM波形,经过前面所述的扇区判断和时间计算后,就可以对ePWM模块进行配置使其输出PWM波形。在进行配置时Sx1与Sx3互补输出,Sx2与Sx4互补输出,因此只需要配置Sx1和Sx2的比较寄存器(CMPR)。如图6所示,为N = 1,M = 1时的输出PWM波,其中:
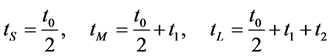 (7)
(7)
同理可以得到其他扇区内的比较寄存器的配置如表6所示。
5. 仿真与实验
5.1. 仿真结果
如图7所示为三相负载上的电压、三相参考电压和三相负载中点与直流母线电容中点之间的电压波形图。由仿真结果可以看出,三相负载上的PWM波形能够很好的跟踪参考电压。
5.2. 实验结果
为进一步对提出的控制方法进行验证,搭建了以TMS320F28335为核心的并网逆变器器三相电网不平衡试验平台。实验容量为10 kw的并网逆变器,实验参数如下:WPAP330150交流电网模拟电源和150 kw直流模拟电源,最大直流功率和交流功率都为150 kw,TPS2014通道隔离示波器。
利用本文提出的SVPWM简化算法,在逆变器滤波前后的波形如图8所示,波形说明本算法能方便的生成三电平波形,波形准确、计算简洁方便,进一步说明本算法简化了扇区判断和时间计算,降低了硬件资源的需求。

Figure 6. PWM waveform
图6. PWM波形

Table 5. Time calculation of six triangle section
表5. 六个三角形扇区的时间计算

Table 6. Configuration of CMPR
表6. 比较寄存器配置
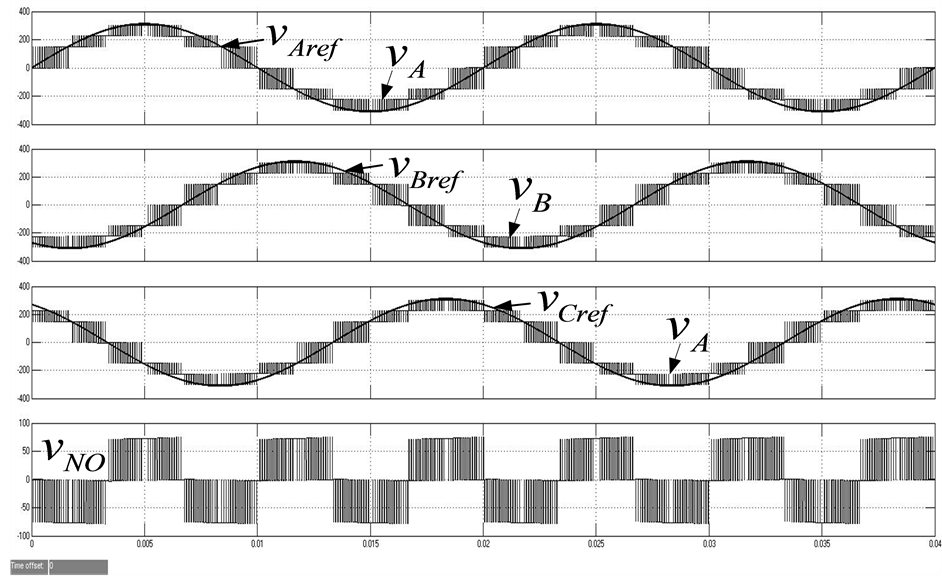
Figure 7. Simulation waveform
图7. 仿真输出波形
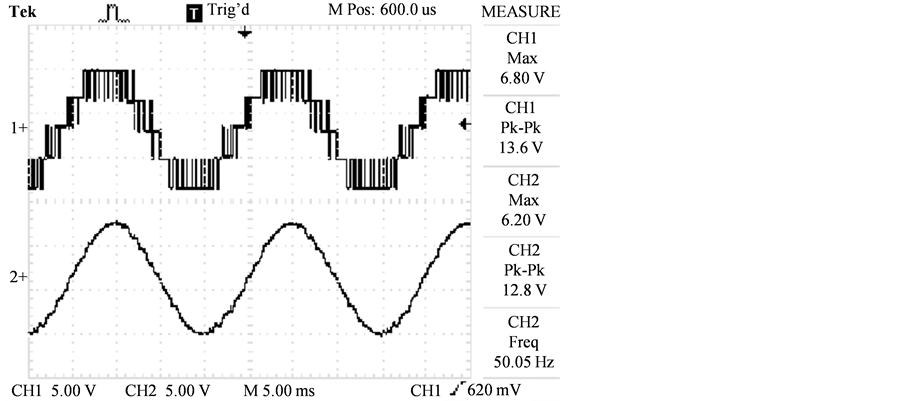
Figure 8. Experimental waveform
图8. 实验波形
6. 结论
本文对简化三电平SVPWM的DSP实现方法进行了研究,给出了详细的DSP实现方法.由于将三电平矢量空间转化到了两电平的矢量空间,每个小六边形的两电平算法相同且都不涉及复杂的三角函数运算等,因此扇区判断以及时间计算都大大简化。通过仿真和实验可以看出,该算法相应速度高,能够精确跟踪给定的参考电压。