1. 引言
可分离交易可转债(Warrant Bonds,简称WBS)是上市公司发行的一种将认股权证和债券结合在一起的特殊债券,即一种“认股权证和债券分离交易的可转换公司债券”。可分离交易可转债是债券与股票权证的混合融资品种,它由两大部分组成,一是债券,二是股票权证。它在发行时规定其持有人有权在保持债券有效性的前提下,在债券到期日(或到期前的一定期间内)按照事先约定的某个约定价格(即行权价格)及行权比例,认购发行公司的股票。可分离交易可转债与普通可转债的本质区别在于债券与期权可分离交易,即分离交易可转债的持有者在行使了认股权利后,其债权依然存在,仍可持有到期收回本金并获得利息;而普通可转债的投资者一旦行使了认股权利,则其债权就不复存在了。因此,可分离交易可转债可理解成“买债券送权证”的创新品种。
可分离交易可转债作为一种融资方式创新,最早出现在20世纪70年代的美国证券市场上,目前在西方发达国家已经是一种比较成熟的衍生金融工具。在我国资本市场上,可分离交易可转债还是一个全新的金融产品。2006年5月7日,《上市公司证券发行管理办法》首次将可分离交易可转债列为上市公司再融资品种,可分离交易可转债开始受到人们的关注。短短几个月间,马钢股份、武钢股份、新钢钒、唐钢股份、中化国际、云天化、深高速等7家上市公司纷纷提出发行可分离交易可转债的申请并公告计划通过这一新的金融创新产品融资234亿元,这使得分离交易可转债成为资本市场中不容忽视的一只力量,预示着可转债市场更为广阔的发展空间,可分离交易可转债的定价问题已经成为可转债研究领域的一项重要研究内容。
20世纪70年代,可分离交易可转债在美国刚出现时,很多国外学者认为它将会成为普通可转债的替代品。于是,当时的国外学者们对可分离交易可转债的研究主要是侧重于与普通可转债(CBS)进行比较。Ingersoll(1977) [1] 提出可以用债券和认股权证组合成与可转换债券等效的融资组合。Finnerty(1986) [2] 对七个参与可分离交易可转债交易的机构投资者进行问卷调查,结果显示,附带权证带来的初始发行折价会使投资者面临税收负担,如果税负不断增加,很多投资者将不会投资可分离交易可转债。而Payne [3] 则对可分离交易可转债与普通可转债的关系进行了全面的比较研究。近年来,国内学者对可分离交易可转债的定价也做了一些积极的探索。许可、李听(2007) [4] 在《“马钢”可分离可转债定价实证分析》中以国内首支认股权和债券分离交易的可转换公司债券——马钢可转债为样本,从实证角度对其进行了定价分析。化宏宇、程希骏(2008) [5] 认为可分离交易可转债中权证是一种简单的百慕大式权证,他们根据风险中性定价原理,考虑在完备的市场下按照收益最大化原则,结合鞅定价原理,给出了权证理论上的价格。李争华(2008) [6] 利用有稀释效应的B-S模型对08年上市的宝钢可分离交易可转债进行定价研究,并做了简单的实证分析,得出的结论是宝钢可分离交易可转债的债券部分定价效果很好,认股权证市场价格偏高。骆桦、沈红梅[7] 结合几只具体可分离交易可转换债券研究了WBS在我国的实际应用。
我国学者朱丹(2011) [8] 从定量的角度分析了可分离交易可转换债券的价值构成,利用鞅定价方法推导出其定价公式。但是朱丹运用的模型存在两个不足,第一、使用Vasicek随机利率模型;该利率模型是均值回归模型,有可能使利率变为负值;第二、就是假定分离交易可转债对应的基本股票服从几何布朗运动,这意味着股票价格变化是相互独立的随机变量,并且资产收益率服从正态分布,这不符合股票价格波动的实际情况。因为大量金融实证研究和行为金融学研究表明,股票价格变化不是随机游走,而是不同时间呈现不同程度的的长期相关性,并且资产收益率的分布也不是正态分布,而是具有“尖峰厚尾”的特性,这是金融资产收益的典型特征。由于Peter(1994)应用R/S分析法证明了分数布朗运动不依赖于独立及正态分布的假设,它的特征指数以及尺度参数等能很好地刻画金融市场波动性、股票价格的一般行为过程及资产收益率的“尖峰厚尾”分布等。此外,分数布朗运动具有的自相似性和长期依赖性,与人们对金融市场的直观感觉是一致的,即未来时刻股票的价格不仅与现在价格有关,还与过去相当一段时间的价格有关[9] 。为了克服前人提出的可分离交易可转换债券定价模型中的两个不足,本文将在下文中运用随机利率服从Hull-White模型[10] 以及标的股票遵循分数布朗运动来对前人提出的可分离交易可转换债券定价模型进行改进,建立一个双分数布朗运动下的可分离交易可转债的定价模型,并运用风险中性定价理论推导出可分离交易可转债的定价公式。
2. 预备知识
2.1. 可分离交易可转债的构成要素
一般说来,可分离交易可转债具有以下一些要素:
1) 基本股票:它是可转换债券的标的物,即可转换债券可以转换成的那种股票。
2) 票面利率:它给予投资者一个最低收益的保证,但通常低于普通债券利率和银行利率;对于可分离交易可转债,债券认购人在购买时将无偿获得一定数额的认股权证。
3) 附权证比例:指一份债券可以无偿获得的认股权证的数量。比如某可分离交易可转债的附权证比例为0.4,那么10份债券可以配送4份认购权证。
4) 行权期限:指认股权证的有效期限。在此期限内,债券持有人可随时按约定的行权价格行使该权利,也可以放弃该权利。
5) 行权比例:指1份权证可以购买的标的股票数量。比如某认购权证的行权比例为0.5,那么10份权证可以买入5股股票。
6) 行权价格:即转换价格,是指权证持有人在行使认购权时购买每股股票的约定价格。
2.2. 可分离交易可转债的价值构成
可分离交易可转债的价值由两部分构成:单纯的债券价值和以股票为标的物的看涨期权价值。其到期现金流量(或到期值)以公式表示如下:
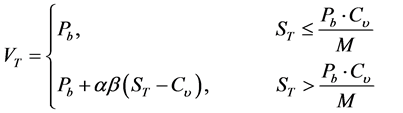
其中,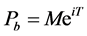 代表以票面利率为
代表以票面利率为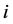 (常数)计算的单纯的债券价值,
(常数)计算的单纯的债券价值,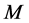 表示可转债的面值,
表示可转债的面值,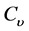 表示约定的行权价格(即转换价格),
表示约定的行权价格(即转换价格), 表示到期时间,
表示到期时间,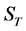 表示
表示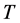 时刻的股价,
时刻的股价,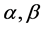 分别表示附权证比例及行权比例。
分别表示附权证比例及行权比例。
2.3. 分数布朗运动的定义
令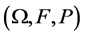 是一完备概率空间,设
是一完备概率空间,设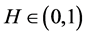 为一常数,称一高斯过程
为一常数,称一高斯过程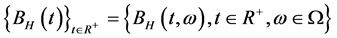 是带Hurst参数为
是带Hurst参数为 的分数布朗运动,如果满足,
的分数布朗运动,如果满足,
1)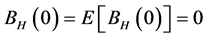 ,对所有的
,对所有的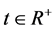 ,
,
2) ,对所有的
,对所有的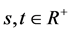 ,其中
,其中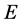 表示概率测度
表示概率测度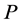 下随机变量的期望,
下随机变量的期望,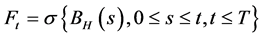 。注意到当
。注意到当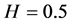 时,分数布朗运动就是标准布朗运动。
时,分数布朗运动就是标准布朗运动。
根据分数布朗运动的基本理论[11] ,存在一个标准布朗运动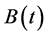 ,有
,有 ,其中算子
,其中算子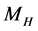 的定义如下[11] :
的定义如下[11] :
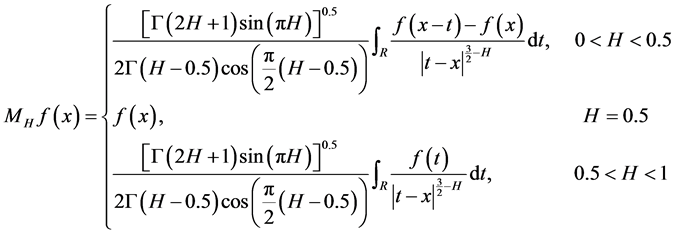
定义[10] :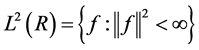 ,并定义:
,并定义: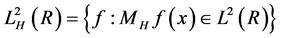 。
。
2.4. 引理1
设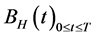 是概率空间
是概率空间 上的分数布朗运动,
上的分数布朗运动,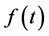 是一个非随机的时间的函数,则
是一个非随机的时间的函数,则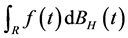 是高斯过程,且满足如下性质:
是高斯过程,且满足如下性质:
1) 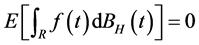
2) (分数次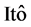 等距性)[12] 若
等距性)[12] 若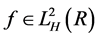 ,则有
,则有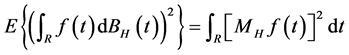
2.5. 引理2 [13]
设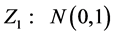 ,
,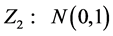 ,
,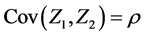 ,则对任意的实数
,则对任意的实数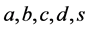 ,有下式成立:
,有下式成立:
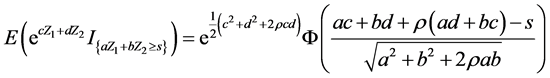
其中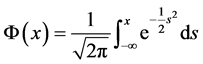 表示标准正态分布函数,证明参见[13] [14] 。
表示标准正态分布函数,证明参见[13] [14] 。
3. 金融市场模型
3.1. 模型假设
1) 证券市场没有交易成本和税收,并且所有证券是完全可分的;
2) 证券交易是连续进行的;
3) 不存在无风险套利机会;
4) 债券利息按连续复利计算;
5) 可转债无违约风险。
3.2. 可分离交易可转债的定价模型
1) 无风险利率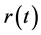 是随机的,且满足金融学中的Hull-White模型:
是随机的,且满足金融学中的Hull-White模型:
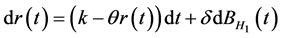 (1)
(1)
其中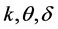 是正常数,
是正常数,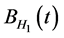 是Hurst参数为
是Hurst参数为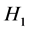 的分数布朗运动。
的分数布朗运动。
2) 可分离交易可转债对应的基本股票的价格 也遵循几何分数布朗运动,即满足如下微分方程:
也遵循几何分数布朗运动,即满足如下微分方程:
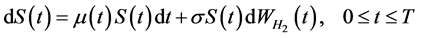 (2)
(2)
其中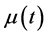 表示股票价格过程在时刻
表示股票价格过程在时刻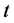 的瞬时期望报酬率,
的瞬时期望报酬率,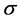 表示股票价格过程的波动率,
表示股票价格过程的波动率,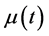 为
为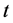 的
的
函数;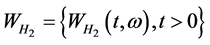 是Hurst参数为
是Hurst参数为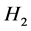 的分数布朗运动,
的分数布朗运动, 表示可分离交易可转债的到期日,
表示可分离交易可转债的到期日,
假定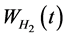 与
与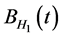 相互独立。在风险中性世界里,我们有
相互独立。在风险中性世界里,我们有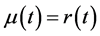 ,于是式(2)可化为:
,于是式(2)可化为:
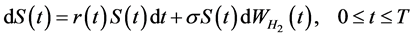 (3)
(3)
3.3. 引理3(分数型 公式)[15]
公式)[15]
设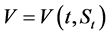 ,
,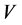 是二元可微函数。若随机过程满足
是二元可微函数。若随机过程满足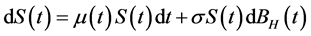 ,
,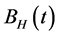 是Hurst参数为
是Hurst参数为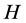 的分数布朗运动,则
的分数布朗运动,则
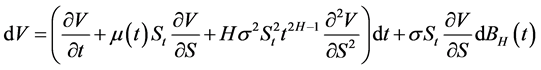
证明:根据Taylor公式有: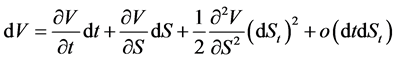 ,
,
由于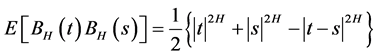 ,所以
,所以 ,即
,即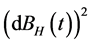 近似为:
近似为: ,则有:
,则有:
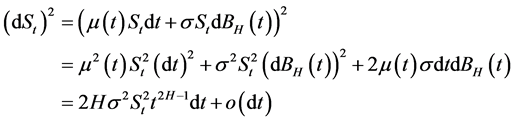
忽略高阶无穷小,从而得到
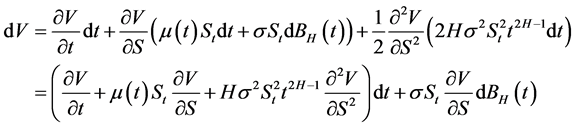
3.4. 定理1
随机微分方程(1)的解为:对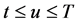 ,
,
 (4)
(4)
证明:令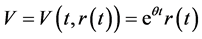 ,由分数型
,由分数型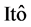 公式可得:
公式可得:

将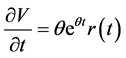 ,
, ,
,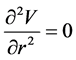 代入上式得:
代入上式得:
 ,
,
从而,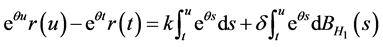 ,故式(4)成立。
,故式(4)成立。
由式(4)可得:
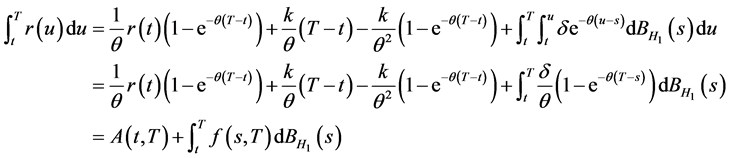
其中: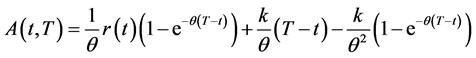 ,
, 。
。
由引理1可知, 是一个正态随机变量,且
是一个正态随机变量,且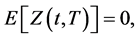
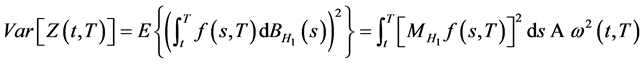 。
。
3.5. 定理2
随机微分方程(3)的解为:
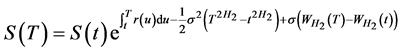 (5)
(5)
证明:由分数型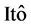 公式可得:
公式可得:
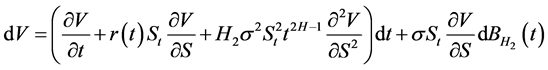 ,
,
将 ,
,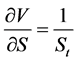 ,
,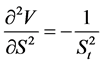 代入上式,即得:
代入上式,即得:
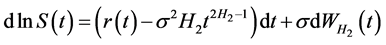
于是,
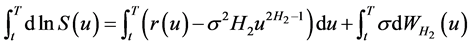 ,
,
故定理2成立。
而且由定理1可得: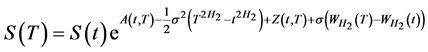 。
。
4. 双分数布朗运动下可分离交易可转债的定价公式
4.1. 定理3
在随机利率和基本股票价格分别遵循两个相互独立的分数布朗运动(1)和(3)的条件下,可分离交易可转债在到期前任意时刻 的价值为:
的价值为:
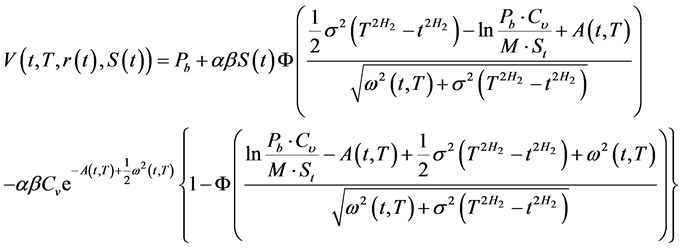 (6)
(6)
证明:由风险中性定价原理(即无套利定价原理)可知,
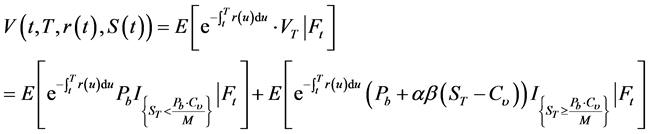
令上式中的第一、二大项分别为 ,先计算
,先计算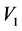 ,
,

由定理1可知: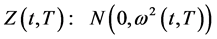 ,且
,且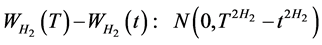 [16] ,则
[16] ,则
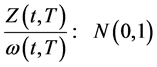 ,
,
且由于 与
与 相互独立,
相互独立,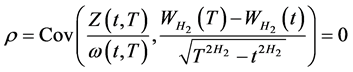
于是,由引理2:
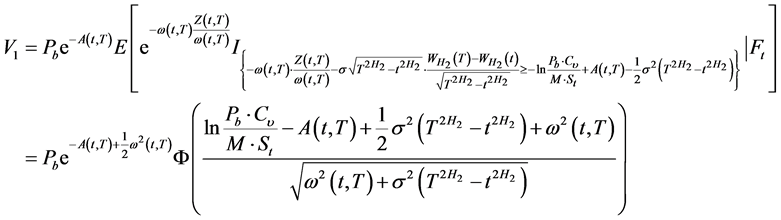 (7)
(7)
再计算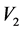 ,
,
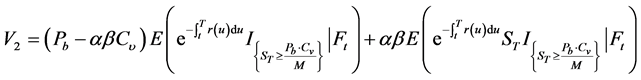 (8)
(8)
将上式(8)中的右边两项分别记为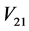 ,
,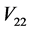 ,则
,则 与
与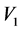 的计算方法相同,可得:
的计算方法相同,可得:
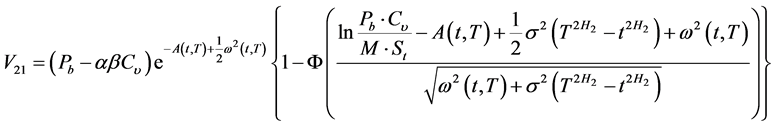 (9)
(9)
由定理2可得:
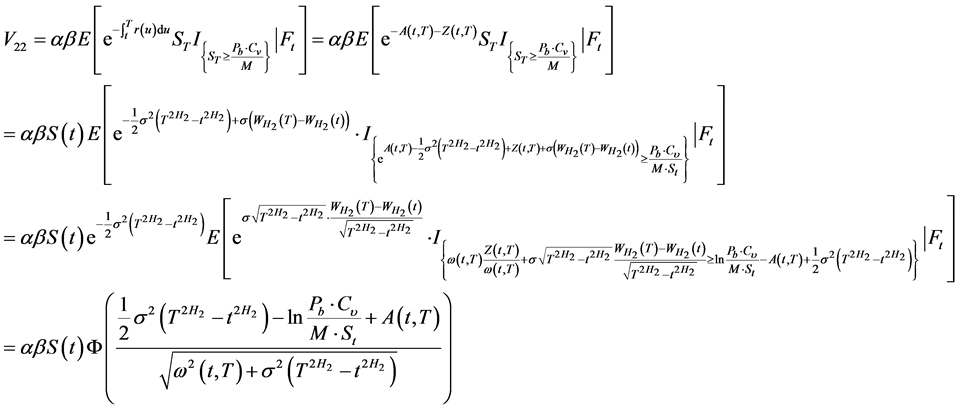 (10)
(10)
将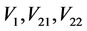 分别代入
分别代入 中,得到:
中,得到:

4.2. 推论
双分数布朗运动下可分离交易可转换债券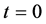 的价值为:
的价值为:
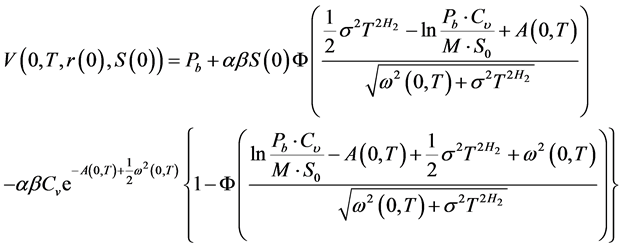 (11)
(11)
5. 结束语
本文在克服前人所提出的关于可分离交易可转债定价模型的不足的基础上,借鉴了已为大量金融实证研究所验证的金融资产波动遵循分数布朗运动的经验,建立了更加贴近金融市场实际的可分离交易可转债的定价模型,并运用风险中性定价原理(即无套利定价原理),获得了随机利率和标的股票价格分别遵循两个相互独立的分数布朗运动的条件下债权与转股权可分离交易的可转债的定价公式。对于年轻的中国证券市场而言,可分离交易可转债是一个极具发展潜力的新型金融衍生产品,它对拓宽企业融资渠道、丰富证券品种和繁荣证券市场,都将起到积极的作用。因此,如何给可分离交易可转债以科学的定价将是十分重要的,值得我们共同去探讨和研究。