1. 引言
车辆路径问题(Vehicle Routing Problem, VRP)是物流网络中一个重要的优化问题,由Dantzig和Ramser [1] 在1959年首次提出,经典的车辆路径问题可描述为:从一个配送中心向分散在周围的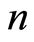 个客户派遣
个客户派遣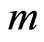 辆车来配送货物,保证每个客户只被一辆车访问且仅访问一次,求确定每辆车的行车路线和最小成本,该成本可以是最短路径,最小费用或者最小运输成本。在具体研究中,车辆路径问题有多种形式,如具有容量限制的车辆路径问题(Capacitated Vehicle Routing Problem, CVRP) [2] 、带有时间窗的车辆路径问题(Vehicle Routing Problem with Time Window, VRPTW) [3] ,同时送取货的车辆路径问题(Vehicle Routing Problem with Simultaneous Pickup and Delivery, VRPSPD) [4] 等。
辆车来配送货物,保证每个客户只被一辆车访问且仅访问一次,求确定每辆车的行车路线和最小成本,该成本可以是最短路径,最小费用或者最小运输成本。在具体研究中,车辆路径问题有多种形式,如具有容量限制的车辆路径问题(Capacitated Vehicle Routing Problem, CVRP) [2] 、带有时间窗的车辆路径问题(Vehicle Routing Problem with Time Window, VRPTW) [3] ,同时送取货的车辆路径问题(Vehicle Routing Problem with Simultaneous Pickup and Delivery, VRPSPD) [4] 等。
Lenstra和Rinnooy Kan [5] 证明了几乎所有类型的VRP均为NP-Hard问题。Savelsbergh [6] 和Solomon [7] 指出带时间窗的VRP由于要考虑送货时间,所以比一般的VRP更复杂。车辆路径问题被提出来后,设计高效的求解算法一直是该问题研究的重点和难点。车辆路径问题的传统算法大致分为两大类:精确法和近似法。精确法指可以求出其精确最优解的算法,包括分支定界法(Branch and Bound, BB) [8] 、动态规划法(Dynamic Programming Method, DP) [9] 等;近似法包括分散搜索算法(Scatter Search, SS) [10] 、遗传算法(Genetic Algorithm, GA) [11] 等。由于该问题是NP难问题,因此,对于规模较大的情形,分支定界法、动态规划法等精确算法一般无法在指定时间内给出全局最优解,而近似法虽然无法保证给出精确的全局最优解,但能在指定时间内获得一个满意解或近似解。基于群体搜索的最优化算法,在求解复杂优化问题时,能有效跳出局部最优解,有较强的全局搜索能力。近年来,以遗传算法为代表的智能优化算法已成为求解该类复杂组合优化问题的有效算法之一。
谢秉磊[12] 构建了考虑车辆容量约束的随机旅行时间规划模型,提出了求解该问题的遗传算法。文[13] 基于模糊逻辑给出了一个求解具有多配送中心车辆路径问题的遗传算法。对于大规模的车辆路径问题,文[14] 给出了一个变邻域启发式搜索算法。文[15] 针对单车场多送货点的车辆路径问题,给出了一个遗传算法,通过改进交叉和变异算子,提高了算法的搜索效率。文[16] 通过引入一个新的交叉算子给出了求解VRP问题的遗传算法。
本文研究带容量限制的车辆路径问题(Capacitated Vehicle routing problem, CVRP),CVRP要求满足以下条件及假设:1) 所有的配送车辆以配送中心为起点和终点;2) 每条配送路径上各客户点的需求量之和不超过车辆的负载量;3) 每个客户的需求仅由一辆车一次满足。众所周知,对于复杂的组合优化问题,在算法设计中嵌入适当的局部搜索程序,能有效提高算法的搜索效率[17] 。因此,针对该问题,本文设计了一个基于局部搜索技术的遗传算法。该局部搜索过程通过概率选择要改进的客户组合,通过优化该组合而改进当前路径。实验结果表明,该局部搜索方法能有效提高算法的搜索效率。另外,为了更好地产生新的杂交后代,本文给出了一个基于两个父代个体求和的杂交算子。该算子的特点是即使两个父代个体一样,也能产生不同于父代的一个后代个体。这使得算法在运行后期能有效产生新的后代,保持种群的多样性。
2. CVRP的数学模型
基于文献[18] ,CVRP问题可描述如下:配送中心有 辆车,每辆车的容量为
辆车,每辆车的容量为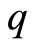 ;配送中心需要为
;配送中心需要为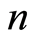 个客户提供货物配送任务,每个客户的需求量为
个客户提供货物配送任务,每个客户的需求量为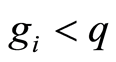
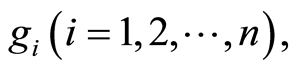 。每个客户由一辆车服务。目标是优化车辆调度,使得在满足货运要求的前提下,最小化车辆的使用及车辆行驶路径,从而节约运输成本。
。每个客户由一辆车服务。目标是优化车辆调度,使得在满足货运要求的前提下,最小化车辆的使用及车辆行驶路径,从而节约运输成本。
将车辆路径问题抽象成图的最短路问题。令配送的编号为0号节点,各客户节点的编号为 ,配送中心车辆的编号为
,配送中心车辆的编号为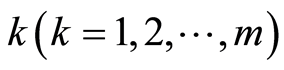 ;令
;令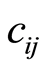 表示各节点之间的距离,并定义如下变量:
表示各节点之间的距离,并定义如下变量:
 ,
,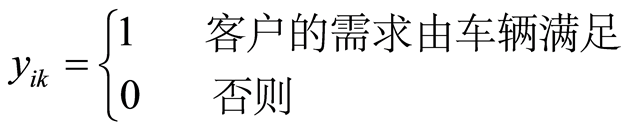 。
。
则车辆路径问题的数学模型如下:
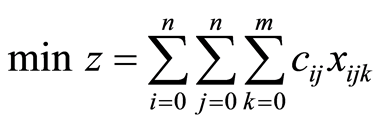 (1)
(1)
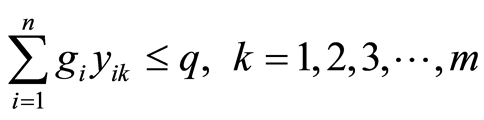 (2)
(2)
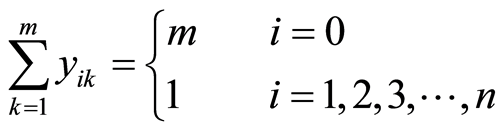 (3)
(3)
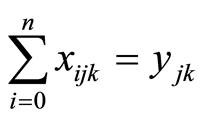 (4)
(4)
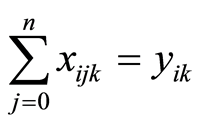 (5)
(5)
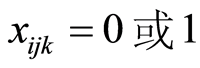 (6)
(6)
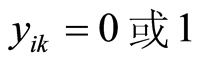 (7)
(7)
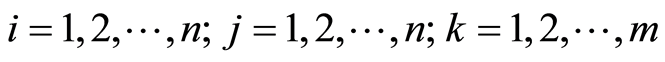 .
.
上述模型中,式(2)表示容量约束,即每条配送路线上的总客户需求量不超过车辆的最大容量;式(3)表示配送任务由m辆车完成,每个客户的配送任务由一辆车完成;式(4)和式(5)意味着:若某一客户由第k辆车提供服务,该车来自某上一客户节点,并且完成服务后离开,到下一客户;式(6)和式(7)表示变量的取值满足0~1整数取值要求。
3. 算法设计
从上述模型可知,求解车辆路径问题的关键是合理确定车辆与各商店的关系,在满足车辆载重量和商店需求约束条件的情况下使得总运距最小。基于这些考虑,设计算法的各个环节。
3.1. 个体编码
本文采用自然数编码[19] 方式表示解的结构,用0表示配送中心,其它自然数表示客户号,如(0 1 2 3 0 4 5 6 0 7 8 9 0),表示用三辆车完成配送任务,配送路径分别为0-1-2-3-0,0-4-5-6-0,0-7-8-9-0。为了计算方便,把0去掉,只用客户编号序列表示解,如上解可表示为(1 2 3 4 5 6 7 8 9)。
3.2. 解码方式
对于给定的编码个体,考虑到尽可能少的利用车辆,采取如下解码方式:首先按编码次序安排第一辆车的配送任务及路径,直到满足容量约束。其次在剩余编码所表示的客户中,按编码次序安排下一辆车的配送任务及路径,直到满足该车的容量约束。依次进行,直至所有客户被安排完。例如,对于编码个体(1 2 3 4 5 6 7 8 9),先安排第一辆车从配送中心0出发,然后为序列中的第一个客户1服务,再考虑约束条件,决定是否为客户2服务,如果不能为客户2服务,则车辆直接从客户1返回配送中心,形成一个配送回路,即0-1-0;若根据容量约束条件,能为客户2服务,而不能为客户3服务,则第一辆车的配送路径为0-1-2-0。当第一辆车的配送路径完成后,依次安排第二辆车、第三辆车等,直到所有任务被安排完为止。该解码方式直接保证当前路径下所用的车辆数最少。
3.3. 初始种群
设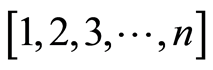 为
为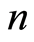 个客户的序号。随机生成
个客户的序号。随机生成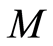 个
个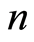 的排列,这
的排列,这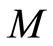 个排列作为个体生成种群规模为
个排列作为个体生成种群规模为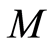 的初始种群。
的初始种群。
3.4. 适应度函数
对种群中每一个体,首先通过解码给出具体的配送路径,代入(1),问题的目标值作为这个个体的适应度。
3.5. 交叉算子
基于给定的编码,在求解CVRP或其它组合优化问题中的遗传算法中,常见的杂交算子有部分匹配杂交(partially matched crossover, PMC) [17] ,循环杂交算子(cycle crossover, CX) [17] 等。
1) 部分匹配杂交按如下方式进行:随机选两个交叉点 ,介于
,介于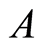 与
与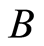 之间的位置称为匹配区,列出匹配区内两个个体基因的对应关系。交换匹配区的元素,并按照匹配区内的对应关系换掉匹配区外的重复位,得两个后代个体。如,
之间的位置称为匹配区,列出匹配区内两个个体基因的对应关系。交换匹配区的元素,并按照匹配区内的对应关系换掉匹配区外的重复位,得两个后代个体。如,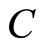 、
、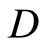 为两个父代个体
为两个父代个体
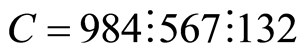
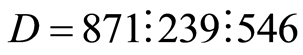
后代为:
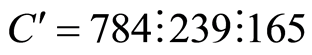
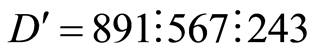
2) 循环杂交算子按如下方式杂交:子代中的第一位取父代个体1的第1位。设子代中的第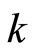 位已经确定,在父代个体1中找出与父代个体2的第
位已经确定,在父代个体1中找出与父代个体2的第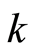 位相同的数,并复制到子代的相应位置。如此反复直到产生出子代,或产生一个循环。若产生一个循环,则找出父代2中与子代中已产生的数不同的数,并按父代2中的顺序填入到子代的剩余位置。如:父代个体为:
位相同的数,并复制到子代的相应位置。如此反复直到产生出子代,或产生一个循环。若产生一个循环,则找出父代2中与子代中已产生的数不同的数,并按父代2中的顺序填入到子代的剩余位置。如:父代个体为:
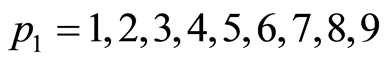
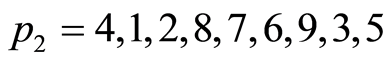
子代个体记为: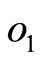 、
、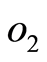 ,计算如下:
,计算如下:
步骤1 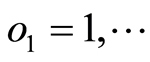
步骤2 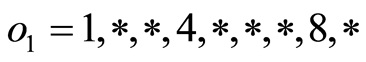
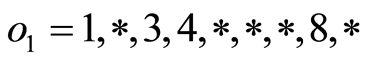

(出现循环)
步骤3 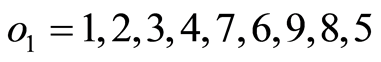
类似可产生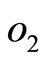
注意到以上杂交算子当父代个体一致时,会产生与父代个体相同的后代个体,这使得在遗传算法运行后期当种群个体趋于一致时,无法产生新的后代个体。为了避免这种情况,本文设计了一个新的杂交算子。具体杂交过程如下:将两个父代个体求和得到的元素取模n,若对应是n的倍数, 则取n。将模n后的元素置于子代,重复的元素删去,最后将所缺元素按父代中的顺序补于子代。
例:n=8,父代个体为:
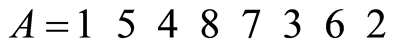
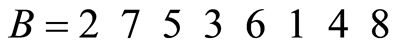
对应元素相加,得: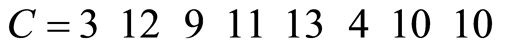
将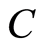 中的每个元素模8。若对应元素是8的倍数,则取8。得:
中的每个元素模8。若对应元素是8的倍数,则取8。得: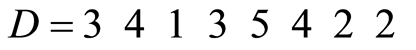
按顺序将重复的数字去掉,得: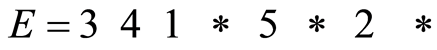
将所缺数字按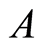 中顺序补于
中顺序补于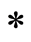 位得:
位得:
当父代个体相同时,不妨取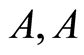 ,得:
,得: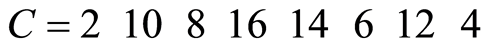
模8,并去掉重复元素,得:
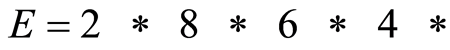
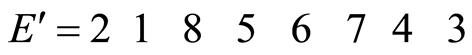
3.6. 变异算子
遗传算法中变异的目的是产生新个体,避免算法早熟收敛。本文采用逆转变异算子[16] 。即在选定区域将基因序列逆转,通过如下例子来描述变异过程:
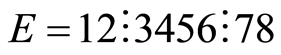

3.7. 局部搜索
很多实际最优化问题是计算复杂的,因此,解决这类问题的方法是在合理的计算时间内找到一个近似最优解。在群智能搜搜算法的设计中,若能嵌入一个基于问题特征的局部搜索过程,则能有效提高算法的搜索效率。本文提出的局部搜索算法是在概率选择的基础上,优化某一辆车的行走路线,使得整个行走路线得到改善。具体过程如下:
1) 在给定的配送方案(个体)中,任选两辆车,车辆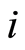 和车辆
和车辆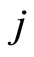 。对车辆
。对车辆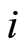 中的任意两个元素置换一次,得到一个新个体;对车辆
中的任意两个元素置换一次,得到一个新个体;对车辆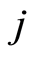 中的任意两个数置换一次,得到另一个新个体。
中的任意两个数置换一次,得到另一个新个体。
2) 新个体选择:若两个新个体均使行车距离缩短,则以较大概率选择缩小幅度大的个体。令缩小幅度分别为: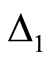 和
和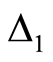 ,则选择概率分别为:
,则选择概率分别为: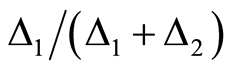 和
和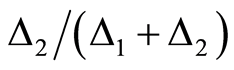 ;若行车距离均增加或一增一减,则选择概率按如下标准给出:第一种情况中增加幅度小的和第二种情况中行车距离减小的,取大概率
;若行车距离均增加或一增一减,则选择概率按如下标准给出:第一种情况中增加幅度小的和第二种情况中行车距离减小的,取大概率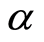 ,对应另一个的选择概率取
,对应另一个的选择概率取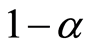 。按赌轮选择选出个体。
。按赌轮选择选出个体。
3) 个体改进:对(2)中选出个体对应的车辆路径全排列,找出最好的一个,得到一个不差于原个体的配送方案。
为了减少计算量,在(3)中,行车路径相同的个体直接删除,如1234的路程和4321的路程一样,因此可以删除一个。事实上,不难看出,按概率分布的车辆选择基于了大概率事件原理和2-锦标赛选择方法。大概率事件原理指出:一次实验中发生的事件是大概率事件。因此,可以认为,在一次置换中若能改进个体,则进一步修正这部分路径可有效改进整个个体的质量。
4. 设计的遗传算法
基于上一部分的设计,本文给出一个基于局部搜索策略的遗传算法(Genetic Algorithm Based on a Local Search Scheme, GA/LSS)。
步1:初始化相关参数,产生初始种群pop(0),令g = 1;
步2:对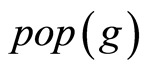 中的个体计算适应度值;
中的个体计算适应度值;
步3:对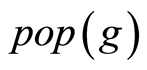 中的个体利用杂交和变异算子产生后代,后代个体集记为O;
中的个体利用杂交和变异算子产生后代,后代个体集记为O;
步4:对O中的个体进行评估,并对较好的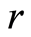 个个体利用局部搜索策略进行修正;
个个体利用局部搜索策略进行修正;
步5:在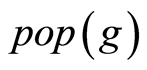 和O中选择较好的
和O中选择较好的 个个体组成下一代种群
个个体组成下一代种群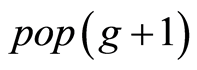 ;
;
步6:若终止条件满足,则停止,输出最优解,否则,令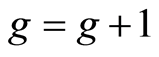 ,转步3。
,转步3。
5. 仿真计算及分析
为了测试提出算法的有效性,本文选择如下算例[16] [18] :有一个配送中心和八个商店,它们之间的相互距离及各商店的商品需求量如表1所示(商店0表示配送中心)。配送中心有两辆载重量为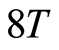 的货车,要求合理安排车辆行驶路径,使总运输距离最小解。该问题的已知最优运距为67.5 [16] [18] 。对于上述问题,本文采用Matlab7.0编程,在CPU的主频2.5 GHz,操作系统为Microsoft Windows XP的PC机上运行程序。设置最大运行代数为50,种群规模
的货车,要求合理安排车辆行驶路径,使总运输距离最小解。该问题的已知最优运距为67.5 [16] [18] 。对于上述问题,本文采用Matlab7.0编程,在CPU的主频2.5 GHz,操作系统为Microsoft Windows XP的PC机上运行程序。设置最大运行代数为50,种群规模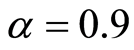
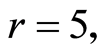
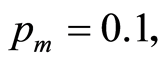

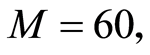 。
。
首先,为了显示本文算法中局部搜索的效率,在GA/LSS中去掉局部搜索过程,并记为GA。比较GA/LSS和GA的计算结果。两种算法各运行10次,计算结果见表2。表2显示,GA/LSS仅有一次没找到最优解,而GA有4次没找到最优解。为了比较收敛速度,选择两种算法都获得最优解的一次计算,给出计算结果的变化趋势,如图1。计算结果:车辆一:[0 6 7 4 0],车辆二:[0 2 8 5 3 1 0],最优运距为67.5。但收敛速度不同,GA/LSS在第9代获得最优解,而GA在第25代获得最优解。

Table 1. Customer’s distance and demand
表1. 客户距离和需求量
为了显示获得最优解时两种算法的计算成本,本文将获得最优运距作为终止条件,计算目标函数的评估次数。表3给出了两种算法运行5次的目标函数评估次数。从结果可以看出,本文所提GA/LSS的目标函值评估次数明显优于GA的次数。即获得最优解的计算成本少于GA。
为了跟文献结果比较,对GA/LSS进行20次运行,计算结果与比较见表4。从表4可以看出,GA/LSS的平均距离以及获得最优解的百分比优于文献结果。


Figure 1. The result of Algorithm optimization
图1. 算法优化示意图

Table 2. Comparison of the calculation results of GA/LASS and GA
表2. GA/LASS和GA的计算结果比较

Table 3. Comparison of the function value of assessment number
表3. 函数值的评估次数比较表

Table 4. The statistical result
表4. 算法结果统计表
6. 结束语
本文讨论了带容量限制的车辆路径问题,设计了求解该问题的遗传算法。该算法的特点是嵌入了一个基于概率选择的局部搜索技术,该技术使得算法的效率明显提高。另外,本文还给出了一个基于父代个体求和的杂交算子,该算子可以使两个相同父代产生不同于父代的后代个体,这使得算法能有效保持种群的多样性。但此算法在同样的迭代次数下,计算的目标函数值次数会比较多。
致 谢
本设计在老师的悉心指导和严格要求下业已完成,从课题选择、方案论证到具体设计和调试,无不凝聚着李老师的心血和汗水,在三年的研究生学习和生活期间,也始终感受着导师的精心指导和无私的关怀,我受益匪浅。在此向李和成老师表示深深的感谢和崇高的敬意。
不积跬步何以至千里,本设计能够顺利的完成,也归功于各位任课老师的认真负责,使我能够很好的掌握和运用专业知识,并在设计中得以体现。正是有了他们的悉心帮助和支持,才使我的毕业论文工作顺利完成,在此向青海师范大学,计算机学院的全体老师表示由衷的谢意。感谢他们三年来的辛勤栽培。
基金项目
国家自然科学基金项目(61463045, 61065009),青海省自然科学基金项目(2013-z-937Q)。