1. 引言
大气污染的一个主要来源就是各种工业固体排放物微粒。燃煤电厂是工业固体排放物的大户之一。燃煤电厂烟气污染物排放到大气中，这不仅关系到环境问题，而且直接危害人们身体的健康。国家对粉尘排放浓度制定了相关的标准，严格控制粉尘浓度，以减少粉尘危害。2011年7月29日，国家环境保护部颁布了更为严格的《火电厂大气污染物排放标准》(GB13223-2011)，现有燃煤发电机组从2014年7月1日起，执行烟尘排放浓度小于30 mg/Nm3的标准[1] [2] 。近年来雾霾现象频繁出现，颗粒物污染严重影响人的健康，PM2.5细颗粒物标准引起重视。实现电厂粉尘浓度有效地在线监测，能更好地掌握粉尘浓度情况，进行有效的降尘除尘，对保护大气环境和人体健康有着重要的作用。
我国粉尘排放监测手段主要采用取样法和非取样法，其中非取样法中常用的黑度法其测量结果的准确性是有疑问的，而且很难用于自动在线监测。取样法中常用的β射线法需要对粉尘进行采样后对比测量，很难实现粉尘浓度的在线监测。现在其它监测仪器也有一些发展，如：一些光电检测的方法，其中光散射理论己经越来越多的应用于分析颗粒的浓度[3] [4] 。目前国内还没有自主生产的可以可靠地在现场连续运行的粉尘浓度测量系统，实现在线测量粉尘浓度是十分必要的。无论从环境保护方面，还是从降低生产成本、减少人力资源耗费、提高测量精度方面，都具有现实意义。
应充分利用现有技术和试验条件，解决国内粉尘浓度传感器存在的问题，开发新型的免维护的粉尘浓度传感器，采用新型的在线监测技术，实现粉尘浓度在线监测的实时性和有效性，不断提高我国粉尘浓度在线监测技术水平。各科研单位及高等院校开展粉尘浓度在线监测技术的研究，对提高我国的污染源监测水平和污染物减排效果具有重要意义[5] -[7] 。本文拟研究锅炉运行参数对我国煤粉锅炉粉尘排放控制的意义。
粉尘浓度与其相关的影响因素之间关系复杂[8] [9] ，因此将支持向量机方法引入粉尘浓度在线监测中，充分利用支持向量机优良的非线性映射和强大的泛化能力，建立粉尘浓度与影响因素之间非线性映射的数学模型，实现粉尘浓度的软测量。
2. 支持向量机软测量方法
支持向量机[10] [11] (Support Vector Machine，简称SVM)适合小样本学习，具有学习速度快、全局最优和推广能力强等优点。该算法在回归预测、时间序列分析、复杂系统建模、函数估计和模型识别等领域得到了广泛应用。因此本文拟利用某机组的历史运行数据，建立基于支持向量回归软测量的粉尘浓度在线监测模型对粉尘浓度进行在线估计，以便较好的跟踪了粉尘浓度的变化趋势。
设给定训练集为
(1)
其中：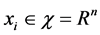
，
，
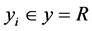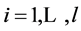。目的是利用该数据集求回归函数
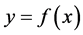。一般用损失函数衡量回归函数
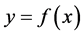偏离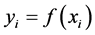
的程度。假定训练集按
上的摸个概率分布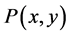
选取的独立同分布的样本点，又设给定损失函数
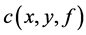，寻求一个函数
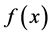使期望风险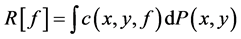
达到极小。
为保证解的稀疏性和回归结果的鲁棒性，采用ε-不敏感损失函数：
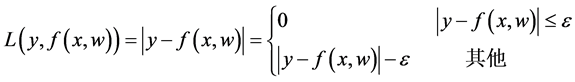(2)
求解下列最优化问题：
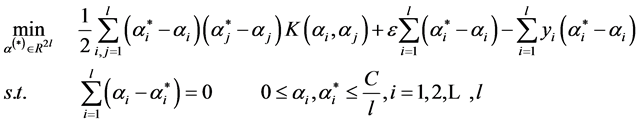(3)
得到最优解，并构造决策函数：
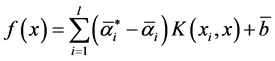(4)
其中，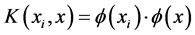
称为核函数，实现将非线性的低维空间的自变量映射到高维特征空间，以实现非线性回归估计。在理论上，只要满足Mercer条件的函数均可以作为核函数。不同核函数的性能和得到的处理结果有所不同。根据经验，本文选择高斯径向基核函数(RBF)：
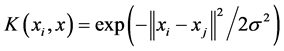(5)
其中：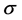
为核函数的宽度参数，控制了核函数的径向作用范围。
3. 基于GA的SVR参数优化
近年来，遗传算法作为一种模拟生物进化和遗传的规律搜索寻优方法，具有通用性强、全局最优、搜索速度快等优点，目前已成为解决各种复杂问题的有力工具[12] 。将遗传算法应用于SVR参数优化的基本步骤如下：
步骤1确定C，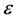
和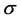
在实际应用中的可能取值范围；
步骤2随机选择各参数的初始值，并采用某种编码构造初始种群P(t)；
步骤3将P(t)中的个体输入SVR模型进行训练，并计算个体适应度函数值；
步骤4判断种群中最优个体的适应度函数值是否满足要求或者达到最大遗传代数，若满足则转至步骤6，否则转入下一步；
步骤5应用选择、交叉以及变异算子产生新的种群，之后返回到步骤3进行迭代；
步骤6输出最佳SVR参数，并通过对训练样本进行训练以获得最佳回归模型。
4. 建模及结果分析
基于支持向量机软测量方法，并利用GA对其进行参数优化，构建粉尘浓度的在线监测模型。采用特征选择方法从众多参数中遴选得到8个主要影响参数作为该模型的输入变量：负荷、总燃料量、再热蒸汽压力、炉膛与风箱差压、烟囱入口烟气流量、排烟温度、二次风量、送风机出口流量，粉尘浓度值作为输出变量。由于本文方法建立的模型是针对同一煤质特性下对粉尘浓度进行研究，且煤质特性不具备实时可读取性，故建立粉尘排放浓度在线监测模型时，煤质特性不作为输入变量。
本文建模所选样本是某电厂600 MW机组2013年3月1日~2013年5月31日之间的70组数据。样本覆盖了锅炉50%~100%负荷范围内的典型运行工况，能很好地满足网络训练对样本集的要求。其中机组负荷在300 MW~400 MW的样本数为12组，机组负荷在400 MW~500 MW的样本数为24组，机组负荷在500 MW~600 MW的样本数为34组。为充分评估所建粉尘排放浓度在线监测神经网络模型的性能，从70组样本数据中随机挑选出63组作为训练样本，剩余7组作为模型的测试样本。
利用SVR模型进行粉尘浓度预测，并用遗传算法对SVR参数进行优化，最终模型的训练曲线如图1所示，所选训练样本点的真实值与模型预测值拟合较好。
在此基础上，利用建立的SVR粉尘浓度预测模型对7组预测样本进行预测，模型预测值与粉尘浓度真实值对比曲线见图2所示。图中曲线对比表明，模型预测值与真实值的变化趋势一致。表1中列出了
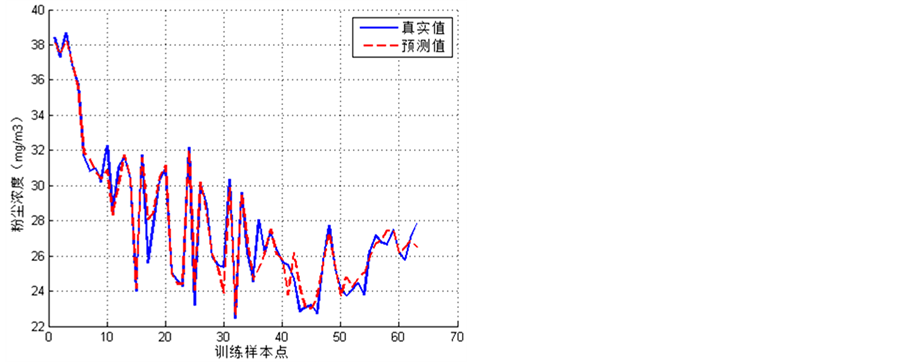
Figure 1. Prediction curve of training samples
图1. 训练样本预测曲线
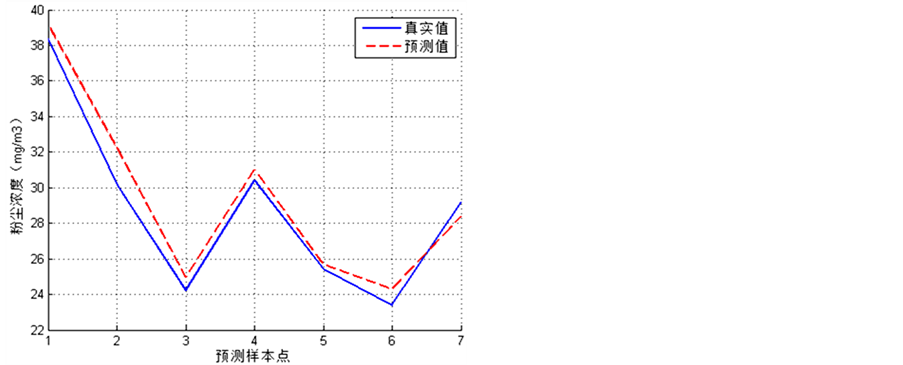
Figure 2. Prediction curve of testing samples
图2. 测试样本预测曲线
Table 1. Comparison of modeling prediction output results
表1. 模型预测输出结果对比
预测样本的真实值，模型预测值，以及相对误差值，便于对比。测试样本相对误差最大为6.81889%，最小为0.95586%，平均误差3.06999%，满足工程需求。仿真结果表明，该模型可以有效的进行粉尘浓度的在线监测。
5. 结论
利用现有技术，挖掘新的监测方法，将软测量方法应用于粉尘浓度监测中，对粉尘浓度进行预测估计，以求解决粉尘浓度难以在线监测的问题。
1) 本文建立了基于支持向量机软测量的粉尘浓度在线监测模型的估计值与实际值吻合较好，较好的跟踪了粉尘浓度的变化趋势。
2) 利用本文建立的模型得到结果与实际值的平均误差为3.06999%。仿真结果表明，该方法为粉尘浓度在线监测提供了一种可供参考的方法，有进一步改进和研究的价值。
NOTES
*通讯作者。