1. 引言
公差–成本模型是描述零件公差值与加工成本之间关系曲线的方程式。对于产品的公差设计来说至关重要,它是设计公差值、估算零部件加工成本的依据[1] [2] 。随着本世纪制造业的迅速发展,涌现了大量的新兴技术和理念,如并行工程、价值工程、敏捷制造等,无一不强调产品设计与成本之间的关系。公差–成本模型越精确,则公差值设计越合理,可以避免精度或成本上的浪费,从而降低加工难度及加工成本。而且,在整个机械产品的设计中,各尺寸链中零部件种类很多,所用到的加工方式也多种多样,没有统一的公差–成本模型也给公差设计带来一定困难。这也是机械设计迈向计算机程序化设计需要解决的问题之一[3] -[5] 。
到上世纪末,对于公差–成本模型的研究,已经有了很多的研究结果。例如,指数模型、负平方模型、幂函数模型等等[6] ,这几种模型虽然很容易建立,但引入了很大的模型误差。Z. Dong等在研究前人成果的基础上提出了混合模型、多项式模型两大类模型。其中混合模型包括幂函数和指数函数混合、直线函数与指数函数混合、B样条函数;多项式模型包含三次、四次、五次多项式,并对各个模型的精确程度进行了比较[7] ,但如果采集的实验点数据不符合多项式特点,采用多项式拟合会产生振荡。S.H. Yeo等提出利用三次样条曲线作为公差–成本模型[8] 。以上模型为公差设计提供了理论依据,但无法完整准确的描述公差与成本之间复杂的数学关系。金秋[9] 从连续复利的角度,对原始的基于加工特征的成本–公差函数进行改进,提出改进的加工成本–公差模型。并通过实例验证了该模型更贴近现实,计算出的总成本更合理。赵罡等采用改进LM (Levenberg-Marquardt)算法来训练BP神经网络,从而模拟公差与成本之间的对应关系[10] ,得到了比较精确的量化模型,但没有在拟合精度上与传统的模型进行比较。而且,以上模型都不是以公差与成本曲线关系的特点为基础来选取基函数进行拟合的。另外,以上方法都是针对提高拟合精度展开的研究,没有相关文献研究过采用一种模型格式拟合多种加工方式曲线。
为了建立精确统一的公差–成本模型,本文在研究公差与成本曲线特点的基础上,提出了采用加权的方法建立加权公差–成本模型。该方法比传统方法得到的模型精度高;不同的加工方式均采用统一的模型形式,更适合于采用计算机进行程序化设计。
2. 公差–成本关系
2.1. 公差–成本经验数据
通过实验方式得到公差与成本的数据是最直接有效的方法。表1为早期估算加工成本所参考的实验数据[7] 。表1中的实验数据分别对应粗加工、半精加工和精加工,如图1所示。从实验数据曲线的趋势可以看出:公差越小,所需要的加工成本便越大,反之则成本越小。
2.2. 现有加工方式的公差–成本数据及模型
机械加工中的加工方式很多,例如常见的车削、铣削、磨削、铸造等,所对应的公差–成本关系也各有差异,但均符合随着公差增大成本减小的趋势。由于表1所整理的实验数据没有明确区分各种加工方式的区别,在核算成本时应用并不多。后来在采集大量实验数据的基础上,绘制了几种加工方式的公差–成本曲线。如图2所示。
目前,在成本与公差实验数据拟合的研究方面,所用到的拟合模型有很多种,见表2。
以上模型中,没有一种模型可以对图2中所有加工方式的拟合都达到满意效果。例如,幂函数对磨削加工的实验数据拟合时比较精确,但对于其他加工方式的拟合就会产生较大的拟合误差。
3. 加权公差–成本模型
降低成本始终是获取经济效益的必要手段,精确计算加工成本显得越来越重要。一个具有实用性的公差–成本模型对公差设计和降低成本起关键作用。为了建立一个拟合精度更高并且适用于多种加工方式的模型,本文在研究各个实验数据曲线特点的基础上,提出了采用加权的方法拟合公差–成本模型。
从图2中可以看出,对于一些加工方式而言,在公差值较小的范围内,随着公差值的减小,成本急剧增加;在公差值较大的范围内,随着公差值的增大,成本趋于常数[11] ;趋于垂直的部分与趋于水平的

Table 1. Experimental data of relative cost-tolerance
表1. 公差–成本实验数据

Figure 1. Curve of experimental data
图1. 加工实验数据曲线

Figure 2. Curves of tolerance-cost for several general manufacturing processes
图2. 几种加工方式的公差–成本曲线

Table 2 Existing models for tolerance-cost
表2. 公差–成本模型列表
部分之间,由一个近似的圆弧过渡。
但是模型的针对性比较强,例如指数模型适于拟合公差值较大的区域里的曲线,即这部分区域内的曲线适合用指数模型进行拟合,这部分区域随着公差值的增大,成本减小的比较缓慢;幂函数适合于拟合公差值小、成本骤升的区域,在不适合的区域,拟合误差就会增大;多项式可使两部分区域实现很好的过渡[11] 。
根据文献[11] 所述,指数函数、幂函数、三次多项式三种基本函数分别适合于拟合一般成本与公差关系曲线的三个阶段,并用实例证实了此结论的正确性。根据以上结论,本论文提出了采用对基本函数加权的方式,提出一种加权公差–成本模型。所采用的基本函数为:
(1) 指数函数:
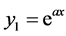 (1)
(1)
(2) 幂函数:
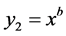 (2)
(2)
(3) 三次多项式:
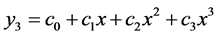 (3)
(3)
以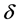 表示公差,
表示公差, 表示成本,则加权公差–成本模型定义为:
表示成本,则加权公差–成本模型定义为:
 (4)
(4)
为了验证加权模型能更精确的拟合出成本与公差之间的关系,采用表1中的实验数据进行验证。根据表1的实验数据,利用多项式模型进行拟合,图3是实验数据曲线和利用多项式模型拟合的曲线。从图3中可以看出,多项式拟合模型的曲线与实验数据曲线之间的存在一定的误差,每个拟合点之间都不重合。把每个对应的拟合点之间的误差计算出来并绘图,如图4所示。可以清晰的看出每种模型与实验数据之间的差值。从图4中可以看出:加权模型每个拟合点处与实验数据差值最小,拟合误差曲线基本与零线重合。
各个模型拟合的优劣可以通过所有拟合点的拟合误差总和来体现,在10组实验数据中,曲线与实际

Figure 3. Real data points and by cubic polynomial model
图3. 多项式对实验数据拟合曲线

Figure 4. Comparison of fitting errors
图4. 模型误差比较
数据的总误差分别为:
指数函数模型总误差:4.8113
幂函数模型总误差:12.2422
多项式模型总误差:17.4851
加权模型总误差:1.0852
就以上模型及数据显示,加权模型的总误差最小,即拟合精度最高。
4. 结论
(1) 提出了选择适合公差–成本曲线特点的指数函数、幂函数和三次多项式作为基函数,利用加权的方式对成本与公差关系曲线进行拟合的方法。采用典型的实验数据对加权公差-成本模型进行了验证,结果证明该方法比以往模型的拟合精度提高80%以上。
(2) 加权公差–成本模型结构形式统一,可以精确拟合多种加工方式的实验数据,有利于计算机程序化设计。
(3) 本文所提出的模型格式,适用于拟合具有随着公差增大而成本降低特点的加工方式,在拟合公差与成本之间具有复杂的非线性关系的加工方式具有一定的局限性。
基金项目
国家科技重大专项(2009ZX04001-141)。