1. 引言
山岳型景区的地貌特征比较特殊,一般岩石占绝大部分,特别是黄山景区岩石占绝大部分。山上靠水库蓄水,水来源于景区降水,因此山岳型景区的水资源是非常宝贵。山下水资源充足,但在干旱季节,山上水资源短缺,需要从山下水库提水,水库之间存在高度差,调水代价比较高。各水库之间的水资源调度问题直接影响到调水开销及供水保障等方面问题,对景区内用水量的预测,结合水库的库容量,可以有效指导水资源的调度分配,在保障供水、生态用水的同时,提高经济效益。
近年来,各地旅游事业的发展,景区之间的竞争激烈,提高景区内的服务质量,有助于提升景区的综合竞争力。景区内部各处都离不开水,山上宾馆,饭店等服务业都离不开水,尤其居民的生活水平在不断提高,对物质生活的要求相对提高,若景区内出现缺水问题,致使大家对景区的印象下降,造成不好的影响。若针对景区用水量进行预测,可以避免缺水现象的发生。
时间序列方法最早起源于1927年,在我国,时间序列分析从70年代末到80年代中后期才得以深入研究和应用。同时,在国内外学者的共同努力下,时间序列分析已经有了新的发展。国外以1976年George E. P. Box和Gwilym M. Jenkins等的专著《Time Series Analysis: Forecasting and Control》 [1] 和1983年S. M. Pandit和Shien Ming Wu的专著《Time Series and System Analysis with Applications》[2] 为标志,国内以1983年安鸿志、陈兆国的专著《时间序列的分析与应用》和1991年杨叔子等著的《时间序列分析的工程应用》等为标志。此外还有很多时间序列分析模型与理论,Esparcia Alcazarn [3] 提出利用遗传算法优化多层神经网络结构,并应用于时间序列预测;Hu Beilain利用前馈神经网络的BP算法对股票交易进行了时间序列预报;赵远光等利用基本遗传算法对BP网络进行优化,对南京月平均气温和降水量进行了预测。在水文方面,时间序列分析应用也比较广泛,如Thomas等以及Yevjevich [4] 最早将AR模型用于河流流量预报。时间序列分析方法在科学、工业、商业、工程和经济等领域有广泛应用,在过去的时间里一直致力于发展和完善预测模型。
随着经济与信息技术的发展,时间序列数据增长量越来越快。吕志涛[5] 提出时间序列具有随机性、周期性、趋势性等的变动特点。山岳型景区用水量具备以上特点,因此通过分析数据,获得相关的变化规律,建立对应模型进行预测。
本文对时间序列分析的研究,针对ARIMA模型及其建模过程进行分析。同时根据其数据的特点,找出合适的模型对其进行预测。其中黄山风景区是典型的山岳型景区,对其用水量进行预测分析进行验证。
2. ARIMA模型基本理论
时间序列分为平稳时间序列和非平稳时间序列[6] ,区别在于均值是否发生变化。对平稳时间序列分析的常见模型包括自回归模型(auto regressive model, AR(p)模型)、移动平均模型(moving average model, MA(q)模型)、自回归移动平均模型[7] (auto regressive moving average model, ARMA(p, q))等3种基本模式。若序列为非平稳序列,但通过d次差分可使序列平稳时,可采用求和自回归移动平均模型,即ARIMA(p, d, q)模型,其中p,d,q分别表示自回归阶数、差分阶数、移动平均阶数。具有自相关跟周期性特征的时间序列,构建季节性ARIMA模型(seasonal ARIMA model)。即SARIMA(p, d, q)(P, D, Q)s,其中P,Q为季节性的自回归和移动平均阶数、D为季节性差分阶数、s为季节周期。
ARIMA模型建模过程步骤[8] 如下:
1) 序列预处理。根据时序图和相关系数值判断序列数据的平稳性。如果序列是白噪声,则具有纯随机性,无建模价值;如果序列是非白噪声,则可直接建立平稳时间序列模型。若序列数据为非平稳序列,则利用差分,季节差分法或者对数转换使其转换为平稳序列,然后进行建模。
2) 模型识别。初始模型定阶是通过判断自相关图与偏相关图[9] 来确定,然后再进一步检验。估计自相关系数p和移动平均阶数q,确定适当的ARIMA模型拟合观察值序列。其中,自相关系数的公式(1)如下:
 (1)
(1)
3) 参数估计。常用的估计方法有矩估计法、最小二乘法、极大似然法和条件最小二乘法等。其中,理论估计效果最好的是极大似然法,但是这种方法实际应用时算法复杂,计算量大。在实际运用中,最常用的是条件最小二乘法。利用以上方法估计ARIMA模型中未知参数,对每一个模型参数是否显著非零进行检验。
4) 模型优化。通常需要调整,也可以同时利用AIC或BIC准则比较各模型的AIC或BIC的值,选取其值最小的作为预测模型,通常此模型被认为是相对最优模型。此过程也可在模型识别的过程中进行,本文采用BIC准则[10] 。
图1是ARIMA模型建模的流程。其中在进行平稳性检测之前,观察数据,看其是否有缺省或异常数据,若有以上情况,需要对其进行预处理。
3. 模型的建立
3.1. 数据预处理
对所获取的数据进行平稳性和随机性检验,数据序列在平稳和非随机的基础上才能建立时间序列模型。纯随机的序列是没有分析价值的,而非平稳的序列可以通过差分化为平稳序列。
首先,绘制黄山用水量的时序图,对时间序列的平稳性进行观察,如图2所示。数据来源于2012年黄山风景区供水有限公司储存数据。在所记载的原始数据中,有部分异常数据,可能是由于某些故障导
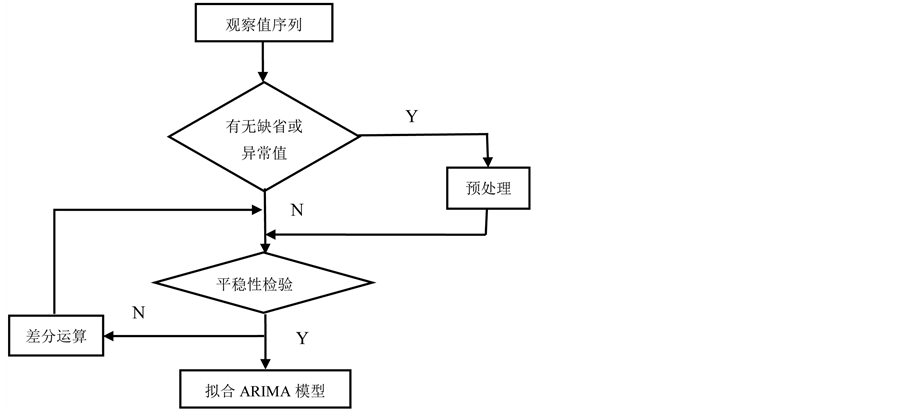
Figure 1. The modeling process
图1. 建模流程
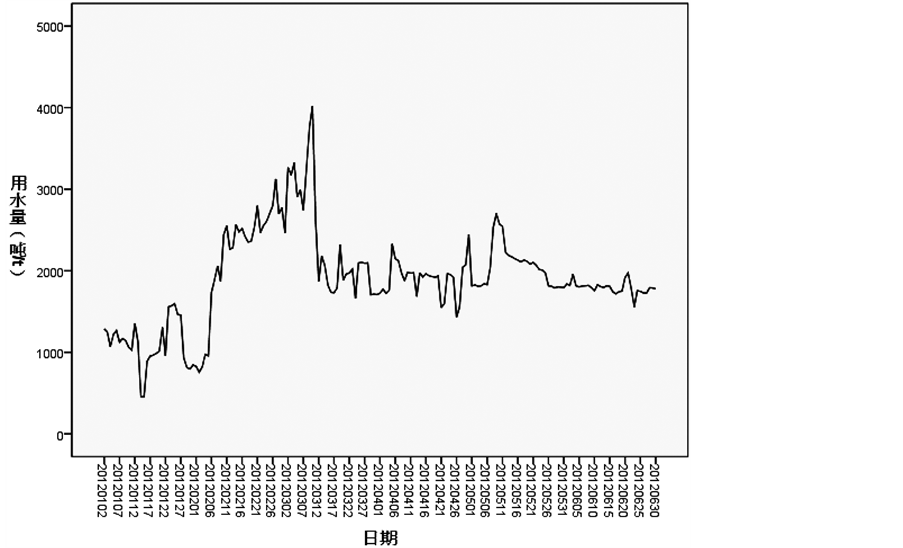
Figure 2. Water consumption observation sequence diagrams
图2. 用水量观测值序列图
致,要对其进行数据处理。根据实际情况考虑,采取当月用水量的平均值代替异常值。
直观看来,用水量趋势是波动的,其均值,方差随时间变化的,此时间序列为非平稳序列。需要对序列进行差分处理,使其序列趋势平稳。经过实验得出,原始数据进行二次差分之后,数据的均值,E(x) = 0,说明差分2次的时间序列具有平稳性。从而得出,ARIMA模型中参数d可取2。
对二次差分序列的纯随机性进行卡方检验,其统计量的P值为0.000 (<0.05),故二次差分序列为非白噪声序列,有建模价值。
3.2. 模型参数确定
对平稳序列进行模型识别是建模的主要过程,即是选择合适的自回归阶数p和移动平均阶数q,估计模型中各项参数,从而建立相应的ARIMA模型拟合观察值序列。参数的设定通常根据数据的自相关以及偏相关系数确定,需要反复试验。在初步确定参数之后,还要检验模型,以便选择到最合适的参数,确定最适合的模型,精确预测值。
利用自相关图和偏自相关图对参数进行判断,再通过BIC准则选定模型。BIC准则是对数据序列进行建模定阶的一种方法,日本统计学家赤池弘次在AIC准则基础上提出来的,是英文Bayesian modification of AIC creterion的简写。若某一阶数使BIC值达到最小,则该阶数定为最佳阶数。上文中,已经确定参数d的取值,因此,尝试不同的p和q值,比较BIC值,取得其中最小值的参数作为模型的参数。
表1是经过实验得出的数据,可以看出当ARIMA(1, 2, 1)时,BIC值最小。根据模型选择的规则,BIC数值最小时,ARIMA模型的拟合效果最好。因此,选择ARIMA(1, 2, 1)模型进行拟合。
4. 实验与结果
为了验证预测数据的有效性,本章同时采用另一种预测方法预测数据,与本文的预测方法比较,体现本文方法的预测准确度。本章选用的另一种预测方法为指数平滑法。指数平滑法是布朗提出的,是在单一时间序列统计模型的基础上进行预测的方法。
同时用ARIMA(1, 2, 1)模型及指数平滑法对2012年黄山风景区上半年时间序列数据进行预测,所得的预测值与实际值拟合精度如图3所示。
图3的横坐标是时间序号,以时间序列代替时间,纵坐标是每天的用水量。从图3中看出两种方法的预测值跟观测值之间的趋势保持一致,初步说明建模的效果基本不错,未出现跟实测数据较大的反差,表明选择的预测方法适合观测值数据本身的特点。图中三条线段有部分重合,说明预测值很接近观测值。
表2是观测值跟两种预测方法所获得的预测值,同时在下表中给出两个预测值跟观测值之间的相对误差。半年的数据总共181条,由于论文中篇幅有限,不能一一列举出,故每月选取两个数值进行比较。具体如表2所示,相对误差保留三个有效位数。
从表2可以看出,两种方法的预测值都比较接近观测值;但根据相对误差可以看出,ARIMA的预测效果要比指数平滑法好。两种方法预测上半年的数据,根据统计可知,指数平滑法的平均相对误差为1.13%,ARIMA模型的平均相对误差大为1.02%。因此,综合以上判断,ARIMA模型适用于黄山风景区用水量的预测中。景区在用水高峰期,根据预测值,可以提前做出应急方案,预防缺水事件发生,保证景区的服务质量。同时,提高景区内的应急处理能力及工作人员的工作效率。

Table 1. BIC value of the ARIMA model parameters
表1. ARIMA模型各参数的BIC值

Table 2. Part of the time series model validation results %
表2. 部分时间序列模型的验证结果%
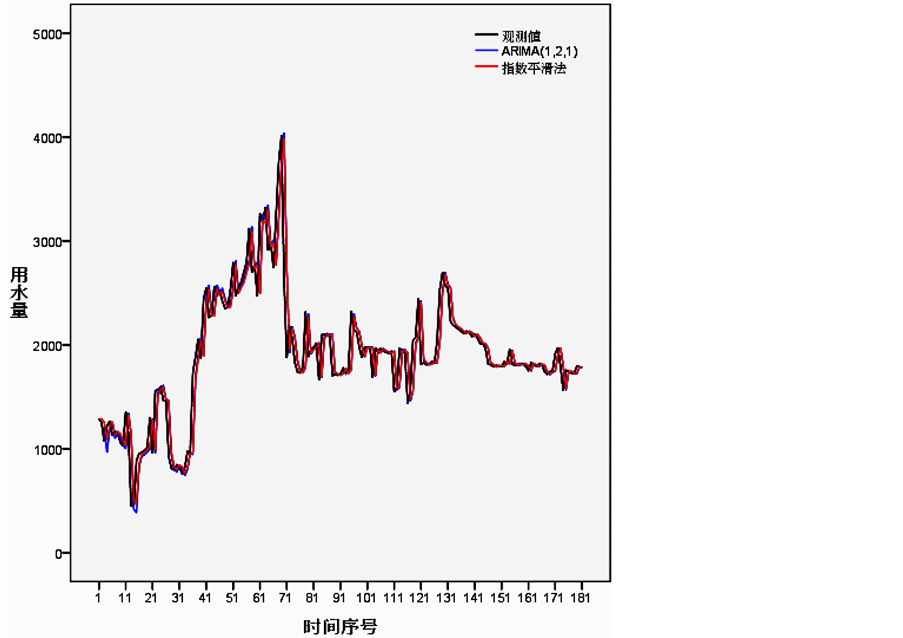
Figure 3. Model fitting results
图3. 模型拟合结果
5. 结论
综上,ARIMA模型是一种有效的统计分析模型,在一定程度上排除人为的主观性,采用更为科学严谨的数学化手段进行预测,具有重要的应用价值。
运用2012年黄山风景区上半年时间序列数据,建立了ARIMA(1, 2, 1)模型并进行预测。通过SPSS19.0软件,对该模型预测的准确性进行了实验检验。结果显示,预测结果较佳。这说明,所建立的ARIMA(1, 2, 1)模型是适合黄山市风景区用水量的发展规律的。
但作为一种数据处理方法,ARIMA模型和其他常用的预测方法一样,主要从数据上反映用水量的统计规律,在实际决策时还应考虑其他综合因素对预测结果的影响,因此,ARIMA还有更广阔的发展以及应用空间。
致 谢
在论文完成之际,我要向我的导师黎杰老师表示衷心的感谢。感谢他在生活和学习中给予我悉心的指导和关怀,他严谨细致、一丝不苟的作风一直是我工作、学习中的榜样,他循序善诱的教导和不拘一格的思路给予我无尽的启迪。在此,我谨向您表示衷心的感谢和诚挚的谢意!
另外,我还要特别感谢路强老师一直以来对我的指导和帮助!感谢黄山风景区凌亮、刘强等工程师,给我了良好的实验环境和项目课题。感谢实验室李强、刘伟等同学对我的帮助,使我得以顺利完成论文。