1. 引言
电力系统负荷一般可分为城市民用负荷、商业负荷、农村负荷、工业负荷及其它负荷等,不同类型的负荷具有不同的特点和规律[1] [2] 。
1) 城市民用负荷主要是城市居民的家用电器及照明,它具有连年增长的趋势及明显的季节性波动特点,而且民用负荷的特点还与居民的日常生活和工作规律紧密相关[3] [4] 。
2) 商业负荷[5] 主要是指商业部门的照明、空调、动力等用电负荷,覆盖面积大,且用电增长平稳,商业负荷同样具有季节性波动的特性。虽然商业负荷在电力负荷中所占比重不及工业负荷和民用负荷,但商业负荷中的照明类负荷占用电力系统用电高峰时段。此外,商业部门由于商业行为在节假日会增加营业时间,从而成为节假日中影响电力负荷的重要因素之一。
3) 工业负荷[6] 是指用于工业生产的用电,一般工业负荷的比重在用电构成中居于首位,它不仅取决于工业用户的工作方式(包括设备利用情况、企业的工作班制等),而且与各行业的行业特点、季节因素都有紧密的联系,一般负荷是比较恒定的。
4) 农村负荷[7] 则是指农村居民用电和农业生产用电。该类负荷与工业负荷相比,受气候、季节等自然条件的影响很大,这是由农业生产的特点所决定的。农业用电负荷也受农作物种类、耕作习惯的影响,但就电网而言,由于农业用电负荷集中的时间与城市工业负荷高峰时间有差别,所以对提高电网负荷率有一定价值。
从以上分析可知,电力负荷具随机性,其有按小时、日、周、变化的特点;同时,负荷又是以日、周、年等为周期不断波动,具有一定的周期性。还有,电力负荷对季节、温度、天气等因素非常敏感,不同的季节、不同地区的气候以及温度的变化都会造成负荷的大幅波动。而对电力负荷预测的方法中回归分析法、趋势分析法适用于大样本,且过去、现在和未来发展模式均一致的预测,灰色模型法适用于贫信息条件下的预测;灰色系统理论采用生成数序列建模。
对电力系统调度、运行人员而言,面对波动起伏的电力负荷,需要制定科学的调度方案以保证负荷的平稳供应,并且需要一定的旋转备用和冷备用,以保证电力系统的充裕性。但是,传统调度方案制定过程中常按最大容量百分数备用或最大机组备用[8] -[10] ,如:N − 1准则,一般无法保证未来调度周期内系统始终保持在一个较高的可靠性水平。如果能够量化电力负荷与各类可靠性指标间的变化规律,并结合已有短期负荷预测技术,避免复杂耗时的可靠性评估过程,快速估计未来系统可靠性水平的变化规律,显然对电力系统调度、运行人员具有重要的参考价值。
鉴于此,本文基于三次样条插值,研究了电力系统可靠性随电力负荷大小的变化规律模型,并结合短期负荷预测技术,进一步建立了电力系统可靠性预测估计模型。
2. 电力系统可靠性评估模型及方法
电力系统可靠性评估具有较大的计算复杂性,它包括3方面的计算:系统状态的获取、状态的系统分析以及可靠性指标计算[10] 。以基于解析枚举法的大电网可靠性评估为例,各指标的形成需要枚举大量的系统故障状态,并需对各故障状态进行系统分析,包括:基本潮流计算,判断是否有元件过载,判断系统是否解列,负荷削减的计算,以及累加形成系统和各负荷点的可靠性指标等。可以看出:电力系统的可靠性计算的核心在于系统分析计算。
在大电网系统可靠性评估中,对每一个要分析的偶然事故都要进行事故后的系统分析。当输电线路故障时,可能导致系统解列,而形成孤立节点或者分裂成若干个彼此孤立的分块子系统独立运行。由于系统的拓扑结构发生了变化,系统正常运行时的节点导纳矩阵等也将随之发生变化,因此增加了事故后潮流分析的复杂性。
在分析计算时,必须首先确定系统是否有解列;如有解列,又必须确定系统中哪些节点和线路属于同一个分块子系统;经过这样的判断后才能形成各分块子系统的拓扑结构,进而确定子系统的导纳矩阵和节点注入功率,最后进行潮流计算。由此可见,系统解列的判断和元件故障后节点导纳矩阵和节点电纳矩阵的形成对于大电网系统可靠性评估来说是一项基本的计算。系统解列及解列后各子系统的形成可用图论的深度优先算法解决。
在计算故障潮流后,便可进行节点电压和线路容量约束的判断,并选择合理的负荷削减方式,进而形成可靠性指标。
2.1. 发输电组合系统可靠性评估方法
电力系统可靠性评估常用方法有状态空间法、事件树法、故障树法、状态枚举法和蒙特卡罗模拟等[11] -[14] 。发输电组合系统可靠性评估的实质就是在各种可能的系统状态下,进行发电系统和主输电网对各用户点提供符合质量要求的供电能力的综合性定量评价。算法的步骤如下:
1) 读入系统数据;
2) 计算正常状态潮流;
3) 枚举或随机抽样故障事件获取系统状态;
4) 判断该状态下系统是否解列,如果解列,则形成各子系统;
5) 判断各子系统电力供给是否充足,如果电力不足,则削减负荷;
6) 计算故障状态的潮流;
7) 电压和元件容量越限检查,如果越限,则削减负荷;
8) 形成状态可靠性指标;
9) 判断故障状态是否枚举完毕或是否已达到足够的抽样精度,如果未完或未达到,转步3);
10) 形成系统总指标。
2.2. 多级负荷模型
本文采用的负荷模型采用按年历次序形成的负荷模型,即包括系统年最大负荷,年内各周的最大负荷,一周7日的日最大负荷和一日24小时的最大负荷。其他负荷按最大负荷的百分数给出。
模拟负荷变化最基本的方式是扫描一年中每个小时的负荷点,以每一负荷水平作为恒定负荷值来计算其充裕度指标,最后通过加权求和计算的年度总指标。一年有8760个小时,如果每个小时的负荷点都需进行充裕度计算,这样的计算复杂性将非常大。因此,在实际中并不采用全枚举的分析方法。
为此,本文采用均值聚类技术产生年负荷的多层模型。假设年负荷模型的8760个负荷点被分为NL个负荷层,每个负荷层的恒定负荷值为该层负荷点的算术平均值。可按如下算法进行:
1) 选择每层负荷的平均初始值
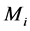 ;
;
2) 计算8760个负荷点
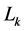 到各负荷层的距离
到各负荷层的距离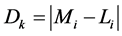 ;
;
3) 把离负荷层最近的负荷点归并到该负荷层,然后计算各负荷层新的平均负荷值:
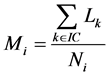 (1)
(1)
式中,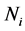 是第
是第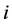 层负荷层的负荷点数目,
层负荷层的负荷点数目,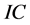 是属于该负荷层的负荷点集合。
是属于该负荷层的负荷点集合。
4) 重复2和3),直到各负荷层的平均值在相邻两次迭代中保持不变。
最后得到的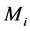 和
和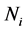 即为第
即为第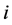 层负荷层的负荷值和负荷点数目。
层负荷层的负荷值和负荷点数目。
需要说明的是:年负荷多层模型所选取的层数应该取一个足够大的值,这样才能充分地接近真实地负荷曲线;但如果层数取得过多,由于各个负荷层都要进行恒定负荷下的充裕度计算,这势必增大计算时间。因此,在选择负荷层数地时候应该追求精度和速度的平衡。
3. 电力系统可靠性随负荷变化规律建模
众所周知,不同的系统负荷水平对应系统不同的系统可靠性水平。为研究系统负荷变化后,系统可靠性的变化规律,本文采用三次样条插值法[15] 对其可靠性评估结果进行样条插值,确保得到连续的系统可靠性随负荷变化的模型。
3.1. 三次样条插值数学模型
设区间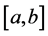 有
有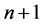 个节点
个节点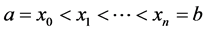 ,其对应的函数值为
,其对应的函数值为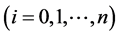
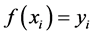 。
。
现求一定义在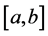 上的函数
上的函数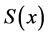 ,使其满足:
,使其满足:
1)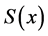 在每一个小区间
在每一个小区间
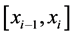 上为三次多项式;
上为三次多项式;
2)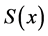 在
在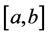 上二阶连续可微,既
上二阶连续可微,既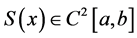 ;
;
3)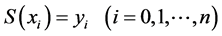 。
。
则称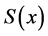 为
为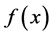 的三次样条函数。
的三次样条函数。
记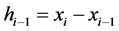 ,求
,求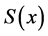 的二阶导函数:
的二阶导函数:
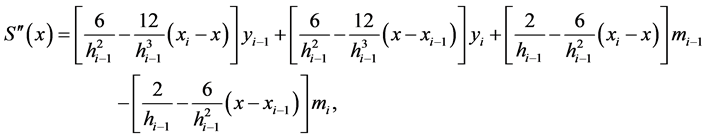 (2)
(2)
所以:
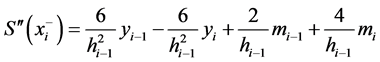 (3)
(3)
再利用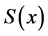 在
在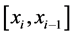 上的表达式可计算出:
上的表达式可计算出:
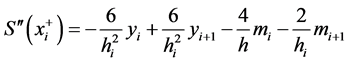 (4)
(4)
由于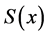 二阶连续可微,即
二阶连续可微,即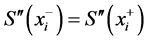 ,得:
,得:

 (5)
(5)
记:
 (6)
(6)
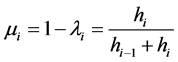 (7)
(7)
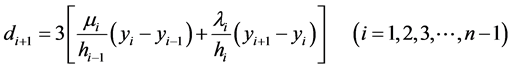 (8)
(8)
将上式整理得方程组
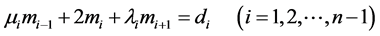 (9)
(9)
这是关于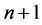 个未知量
个未知量
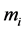 的
的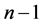 个线性方程组,该方程组有无穷多组解。在实际问题中,往往根据具体情况补充两个附加条件,即端点条件,便可唯一确定一组解,常见的端点条件有:
个线性方程组,该方程组有无穷多组解。在实际问题中,往往根据具体情况补充两个附加条件,即端点条件,便可唯一确定一组解,常见的端点条件有:
1) 曲线在两端点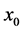 、
、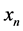 处的导数值已知,即
处的导数值已知,即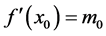 、
、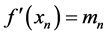 。方程组为
。方程组为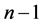 个未知数,
个未知数,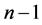 个方程,有唯一解。
个方程,有唯一解。
2) 函数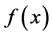 在两端点
在两端点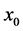 、
、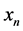 处的二阶导数为0,既
处的二阶导数为0,既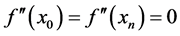 ,即:
,即:
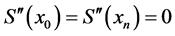 (10)
(10)
由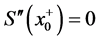 可得
可得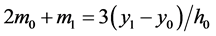 。
。
由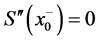 可得
可得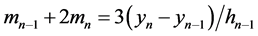 。
。
整理方程组:
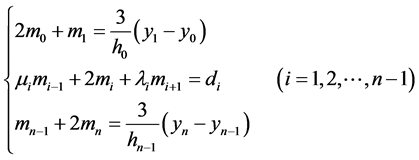 (11)
(11)
方程组也有唯一解。
3) 周期端点条件(当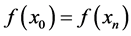 ):
):
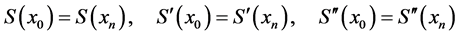 (12)
(12)
于是有:
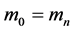 (13)
(13)
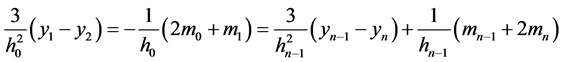 (14)
(14)
与前面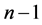 个方程联立,也可唯一求解
个方程联立,也可唯一求解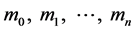 。
。
对于前面两种端点条件所对应的方程组,其矩阵形式为:
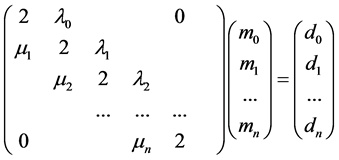 (15)
(15)
该方程组的系数矩阵具有严格对角优势(对角线元素的绝对值大于该行其他元素绝对值之和),其为非奇异阵,故方程组有唯一的解。
3.2. 可靠性随负荷变化的三次样条插值模型
由于插值法是通过一组数据
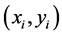 来找出变量
来找出变量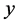 与
与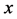 之间的函数关系
之间的函数关系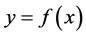 的一个近似表达式。通过函数
的一个近似表达式。通过函数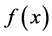 即可对未知数据点的函数值进行近似估计。
即可对未知数据点的函数值进行近似估计。
类似地,基于三次样条插值对系统可靠性与负荷大小间的变化规律进行建模时,可将系统负荷作为自变量,各系统可靠性指标,如LOLP、LOLF、EENS等作为函数值,建立相应的三次样条插值函数。
设插值区间有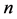 个负荷点(已采用电网峰值负荷进行归一化处理),分别为
个负荷点(已采用电网峰值负荷进行归一化处理),分别为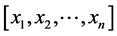 。下面以发电系统LOLP指标为例子说明基于三次样条插值的系统可靠性指标随系统负荷变化规律建模的算法步骤:
。下面以发电系统LOLP指标为例子说明基于三次样条插值的系统可靠性指标随系统负荷变化规律建模的算法步骤:
1) 选择边界条件,本文中均取自然边界条件,即插值区间端点处2阶导数等于0;
2) 采用机组追加法等计算负荷分别为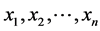 时系统对应的LOLP指标,分别为LOLP0, LOLP1,
时系统对应的LOLP指标,分别为LOLP0, LOLP1, 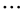 , LOLPn;
, LOLPn;
3) 计算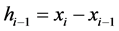 ;
;
4) 根据式(6)-(8)计算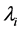 、
、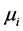 和和
和和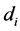 ,
,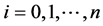 ;
;
5) 求解方程组(5)和(11)或(11)和(15),得到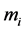 ,
,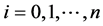 ;
;
6) 将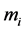 代入分段插值公式,求出各小区间
代入分段插值公式,求出各小区间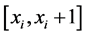 上的样条函数
上的样条函数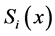 ;
;
7) 计算插值区间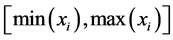 上的样条函数
上的样条函数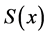 的值,计算结束。
的值,计算结束。
本文研究中,根据负荷大小将插值区间上下界分别取为最大负荷、最小负荷,如[0.5, 1.0],分别计算不同负荷水平时,如:0.5、0.55、0.6、0.65、0.7、0.75、0.8、0.85、0.9、0.95和1.0,系统的可靠性指标。采用三次样条插值分别对各可靠性指标的变化规律进行建模。
4. 算例分析
4.1. 组合系统可靠性指标随负荷变化的规律
下面分别以RBTS测试系统[16] [17] 为例,基于三次样条插值研究系统可靠性指标随负荷变化的规律。表1给出RBTS测试系统发输电组合系统可靠性评估结果。
表2给出RBTS测试系统负荷分别变为0.5、0.55、0.6、0.65、0.7、0.75、0.8、0.85、0.9、0.95、1.0时发输电组合系统LOLP、LOLF、EENS指标计算结果。

Table 1. Reliability indices of RBTS CGTS
表1. RBTS发输电组合系统的可靠性指标
从表2可以看出:与发电系统可靠性评估类似,对发输电组合系统而言,随着负荷的增加,系统可靠性均有不同程度降低。类似地,基于表2的计算结果,图1~图3分别给出RBTS测试系统LOLP、LOLF、EENS指标随负荷大小变化规律的插值曲线,插值间隔为0.01。
从表2可以看出:与发电系统可靠性评估类似,对发输电组合系统而言,随着负荷的增加,系统可靠性均有不同程度降低。类似地,基于表2的计算结果,图1~图3分别给出RBTS测试系统LOLP、LOLF、EENS指标随负荷大小变化规律的插值曲线,插值间隔为0.01。
4.2. 基于短期负荷预测的电力系统可靠性快速估计方法
前面已经指出,电力系统可靠性评估涉及状态枚举、故障潮流计算、负荷削减等过程。状态枚举法随着系统规模的增大计算量呈指数增长,蒙特卡罗法针对高可靠性系统时其收敛速度缓慢,二者均需要超大规模计算量,导致电力系统可靠性评估难以实时在线应用[18] 。

Table 2. Reliability indices with different load levels
表2. 不同负荷的RBTS系统可靠性指标
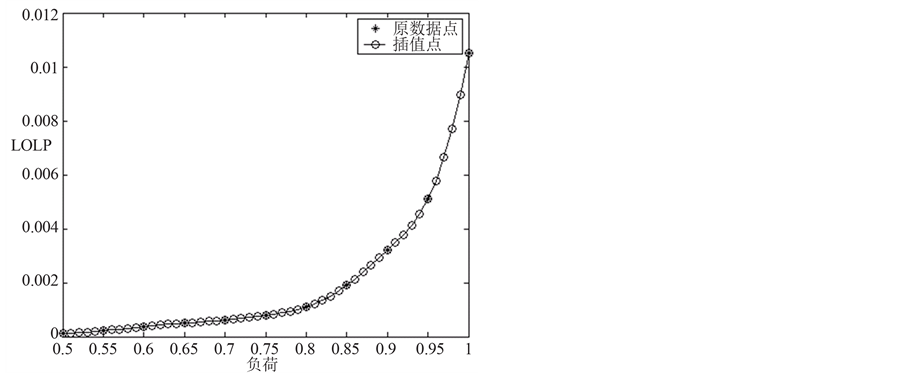
Figure 1. LOLP indices varying with different load levels
图1. LOLP指标随系统负荷变化的规律
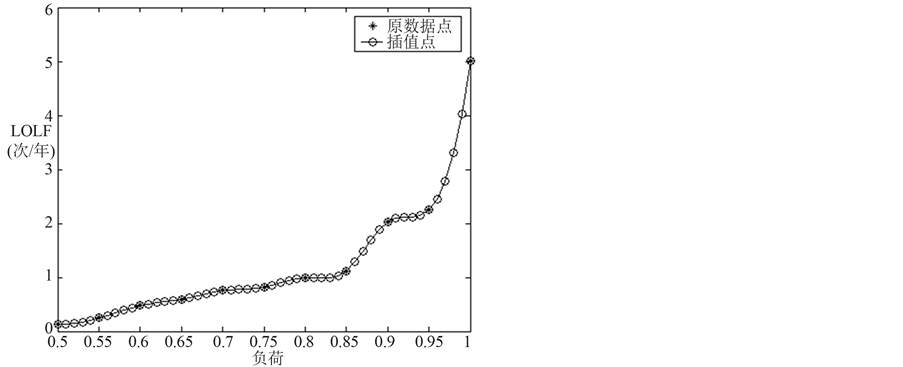
Figure 2. LOLF indices varying with different load levels
图2. LOLF指标随系统负荷变化的规律
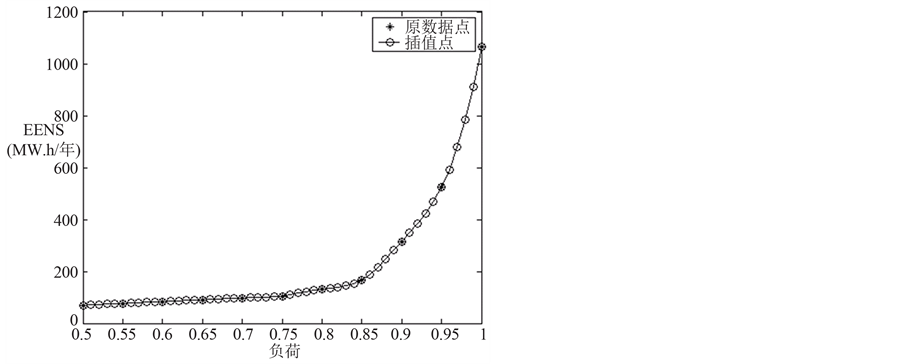
Figure 3. EENS indices varying with different load levels
图3. EENS指标随系统负荷变化的规律
第3部分研究了系统各可靠性指标随负荷变化的规律,并针对不同系统建立了相应的三次样条插值函数,通过插值函数可以对未知负荷大小对应的可靠性指标进行准确估计。为此,本文PSOEM-SVR短期负荷预测方法[19] ,结合样条插值函数,快速估计未来电力系统可靠性变化规律,避免复杂的电力系统可靠性评估过程,为电力系统调度、运行人员提供实时、量化决策依据。
为了验证基于PSOEM-SVR短期负荷预测和三次样条插值进行快速可靠性估计的准确性和可行性,考虑如下三种情形进行(估计)误差分析:
1) 基于某电网7月18日的负荷数据,采用传统可靠性评估方法计算0:00~13:45每隔15分钟系统可靠性指标(真值);
2) 基于7月18日PSOEM-SVR负荷预测值,采用传统可靠性评估方法计算0:00~13:45每隔15分钟系统可靠性指标;
3) 基于7月18日PSOEM-SVR负荷预测值,采用三次样条插值函数估计每隔15分钟的系统可靠性指标。
表3给出了RBTS测试系统EENS指标在三种情形下的计算结果及相对误差值。


Table 3. EENS indices and relative error in three cases
表3. 三种情形下的EENS指标及相对误差
从表3可以看出,若将第(1)种情形下的计算结果作为真值,则第(2)情形和第(3)种情形的预测最大误差可以分别控制在10%和11%以内,且平均相对误差只有1.93%和2.47%,满足工程可靠性预测的精度要求。
其中,第(2)种情形下的预测误差小于第(3)种情形。这主要是第(2)情形中的预测误差主要来源于负荷预测误差的影响,而第(3)种情形预测误差不仅包含负荷预测误差的影响,还包含三次样条插值误差的影响。在工程应用中,可以结合计算时间和计算精度选择第(2)种或第(3)种预测方法。
5. 结论
本文介绍了三次样条插值理论,并给出基于三次样条插值的电力系统可靠性随负荷变化规律建模流程,即首先在插值区间中选择典型负荷点进行可靠性评估计算,然后结合典型负荷点及其对应可靠性指标组成的数据对进行三次样条插值,并对插值函数进行了误差分析和光滑性分析,验证了三次样条插值在电力系统可靠性随负荷变化规律建模过程中的准确性和有效性。
采用RBTS测试系统进行算例分析,算例分析表明:随着负荷增加,系统可靠性均有不同程度的降低,但系统可靠性的降低并非呈线性变化。
另外,结合短期负荷预测数据,基于三次样条插值函数对未来电力系统可靠性水平变化规律进行了快速估计。算例分析表明:基于PSOEM-SVR短期负荷预测和三次样条插值进行快速可靠性估计的平均相对误差只有2.0%左右,完全满足工程可靠性预测的精度要求。