1. 引言
波函数的物理本质是什么?非相对论量子力学,相对论量子力学,规范场论,费曼路径积分,都给出玻恩概率解读,尽管争论激烈,时间长久,却不改变哥本哈根主流地位[1] ;而量子场论一开始则还要赋予波函数物质场含义,尔后再回到概率解读并与实验现象对应[1] 。同一个研究对象在不同理论体系中,本体论地位的不断变更本身就折射出现有理论体系的不完善。
双4维时空量子力学描述克服现有量子理论的先天不足,将实在的物质波贯穿于各种理论的基始[2] 。规范场论中的规范变换是对物理波进行的规范操作,而非数学的概率波,清除了数学波无法发生物理相互作用的认识障碍,规范变换的物理机制变得十分清晰。
微观客体及场的能量、动量量子化,使得定态波函数 是截断、删除(忽略)了本征态之间连续作用的状态波函数[3] ,将微观客体的连续受力运动变成间断的自由运动。定态波函数
是截断、删除(忽略)了本征态之间连续作用的状态波函数[3] ,将微观客体的连续受力运动变成间断的自由运动。定态波函数 被分解成了微观客体的各种自由运动状态——本征态(平面波)
被分解成了微观客体的各种自由运动状态——本征态(平面波) 的叠加态。建在本征态上的坐标系是惯性系,由本征态之间的关系,将引导出惯性系之间的关系。考虑连续作用的介入,能量、动量量子化消失,惯性系将过渡到非惯性系,量子力学可与广义相对论建立起内在的统一联系。
的叠加态。建在本征态上的坐标系是惯性系,由本征态之间的关系,将引导出惯性系之间的关系。考虑连续作用的介入,能量、动量量子化消失,惯性系将过渡到非惯性系,量子力学可与广义相对论建立起内在的统一联系。
2. 时间、空间、质点抽象与物体自身时空结构的关系
2.1. 牛顿力学中的质点属性与坐标系的时空特征
时间、空间是物质的存在形式,既没有脱离物质的时空,也没有脱离时空的物质[4] 。描述物理现象的物理时空是可道之道,有人的认识参与。物理学对物体运动状态的描述,理应包含物体自身的时空特征。物体的运动状态及物体自身的时空特征,必须通过观察发现。观察需要观测信号,物体运动状态及其时空特征,必然带有观测信号的烙印。
任何具体物体都不会是质点。当用信号去观察它时,物体自身的时空特征,与物体的运动状态及观察信号的性质、强弱和传播速度相关。牛顿力学是质点力学。质点模型忽略物体自身的几何形象及其变化,忽略运动及观察信号对物体自身时空特征的影响。在从参照物到坐标系的抽象中,抽掉运动及观察信号对参照物时空特性的影响,就是抽掉物质运动及观察信号对坐标系时空特性的影响。因此,牛顿力学中时空永恒不变,只是物体运动表演的空洞舞台[5] 。这是宏观低速运动对时空的简化与抽象,理论与宏观经验相符。
牛顿时空是均匀平直时空,度规是平直时空度规。相对匀速运动坐标系间的变换是伽利略变换。物理定律在伽利略变换下具有协变性,相对性原理成立。
2.2. 狭义相对论中的质点属性及坐标系的时空特征
爱因斯坦“火车对时”实验中,假设参照物——火车的长度为A'B',并用“闪光”作为观察、记录、认知物体时空的信号。设“火车A'B'”(坐标系K′)与“地面AB”(坐标系K)的中点各自有观察者M′、M [5] 。下面分四种情况进行讨论[6] 。
1) 把火车当成质点。
火车上A′、B′、M′,地面上A、B、M均重合在一起,观察者感知“闪光事件”不需要时间。火车和地面同时性定义相同,t = t′的时空机制即可形成。火车看成质点,火车坐标系K′与地面坐标系K中的时空度量相同。
2) 光速无限大。
光速 ,不管火车长度怎样,运动与否,坐标系K、K′中光通过任何距离都不需要时间。M′、M均同时看到闪光。坐标系K,K′的时空量度相同。把火车当成质点与承认光速无限,时空度量机制等价。牛顿力学中的质点模型,实际上承认有无限大作用信号速度存在。
,不管火车长度怎样,运动与否,坐标系K、K′中光通过任何距离都不需要时间。M′、M均同时看到闪光。坐标系K,K′的时空量度相同。把火车当成质点与承认光速无限,时空度量机制等价。牛顿力学中的质点模型,实际上承认有无限大作用信号速度存在。
光速无穷大,经验上我们只能把物体当成质点。无穷大光速使物体不同部分发出的光全部同时到达观察者,物体的形状及其变化无法区分,只能是一个质点。
3) 火车不动,速度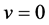 。
。
 ,火车与路基属同一参照系。A′、B′、M′与A、B、M永远重合,不管光速如何,M,M′总是同时收到闪光。坐标系K、K′内的时空量度相同。
,火车与路基属同一参照系。A′、B′、M′与A、B、M永远重合,不管光速如何,M,M′总是同时收到闪光。坐标系K、K′内的时空量度相同。
火车看成质点,对时信号速度无穷大与火车不动,三者在时空机制的建立上都是等价的,可回到伽利略变换。
4) 光速有限,火车有长度A′B′,且以速度 运动。
运动。
爱因斯坦假设火车长为A′B′,且以速度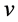 运动,用中点对时方案,推导出坐标系K与K′时空量度的差异。火车坐标系与地面坐标系时空量度的区别依赖于三个前提:一火车不是点,二光速不是无穷大,三火车速度不等于零。上述三个前提条件有形或无形地表现在洛伦兹变换及其数学推导中。
运动,用中点对时方案,推导出坐标系K与K′时空量度的差异。火车坐标系与地面坐标系时空量度的区别依赖于三个前提:一火车不是点,二光速不是无穷大,三火车速度不等于零。上述三个前提条件有形或无形地表现在洛伦兹变换及其数学推导中。
狭义相对论时空亦是均匀平直时空,时空度规与欧氏时空度规有明显区别,所以称为赝欧氏时空。
牛顿力学与狭义相对论相比,在从参照物到坐标系的抽象中,有如下三点重要区别:
其一,牛顿力学在参照物到坐标系的抽象中,忽略物体几何大小和观察信号对同时性的影响。而狭义相对论则考虑参照物的几何大小,把对时信号引起时空量度的变化,通过参照物到坐标系的抽象,将洛伦兹所称运动物体自身的时空收缩演变成了坐标系时空框架的属性,而物体自身则还原成了不变的质点。物体匀速运动,对应的时空均匀平直。
其二,牛顿力学中传递事件发生的信号速度无穷大,物体任何部位发来的信号同时到达观察者,无法感知物体的几何大小,被观察的任何物体只能是质点,除非发光体不同部位不同时发光。狭义相对论中,观察事件发生的信号是光,传播速度有限。理论上讲,传递事件发生的信号速度有限,物体不同部位发来的光(不同事件)不可能同时到达观察者,信号速度有限的世界任何物体都不能看作质点。
其三,牛顿力学中时空绝对不变,讨论质点在永恒不变的时空中的运动规律;狭义相对论不同,时空具有相对性。它把物体因运动而引起的时空量度的变化,在坐标系的抽象中,变成坐标系的固有属性。坐标系变成时空量度随运动状态可变的框架,而物体则还原成了不变的质点。在相对性时空中,讨论质点的运动规律,这就是狭义相对论。
狭义相对论中质点的动量、能量、位置和时间都有确定值,质点的运动具有确定的轨迹。
空间——物质的广延性,由哲学概念转化成为物理概念。狭义相对论显然比牛顿力学前进了一步,考虑了物体的非点特性及信号作用速度的有限性对时空建立的影响,深刻揭示了时空产生的物理机理。
3. 量子力学中的时空特征分析与惯性系
经典波动力学中,一个任意波动 可分解成各种平面波子波
可分解成各种平面波子波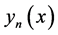 的叠加
的叠加
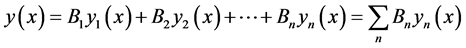
黑体辐射实验和普朗克量子假设是量子力学的基础。但量子力学中微观客体具有波-粒二象性,描述微观客体状态的定态波函数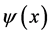 也可以分解成各种本征态
也可以分解成各种本征态 的叠加
的叠加

量子力学中态的叠加原理与经典力学波的叠加原理尽管有质的差别,但叠加态中的“子波或本征态”与“平面波”对应是共同的。氢原子就是一个很好的例案。同时,描述自由微观客体的波包就可看作是一系列平面波的叠加。
原子中,电子在每个能级的能量、动量是量子化的,对于定态波函数, 不随时间改变,即微观客体(电子)在每个能级——本征态中的运动速度
不随时间改变,即微观客体(电子)在每个能级——本征态中的运动速度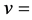 恒量[3] 。可见,本征态对应的是电子自由运动状态,由平面波描述。我们得到结论:定态波函数
恒量[3] 。可见,本征态对应的是电子自由运动状态,由平面波描述。我们得到结论:定态波函数 也可以分解成微观客体的各种自由运动状态——本征态(平面波)
也可以分解成微观客体的各种自由运动状态——本征态(平面波) 的叠加。
的叠加。
微观客体及场的能量、动量量子化,必然造成量子跃迁中相互作用的“间断性”和量子态的“突变性”。所以,理论上讲,定态波函数可看作是截断、删除(忽略)了本征态之间连续作用及状态连续变化的波函数[7] ,它将微观客体在场中的运动状态,通过量子化变成间断的局部自由运动。这样,本征态之间没有时序概念,而其自身又与时间无关,所有本征态可同时并存,并与量子测量假设保持一致。上述本征态的理解,既与经典概念保持了联系,又与量子力学量子假设保持了一致,同时还展现了微观世界物质运动的本质规律。经典力学与量子力学可以相互包容,但认知层面不同,建立的理论不同。
定态波函数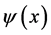 可以分解成微观客体的各种自由运动状态
可以分解成微观客体的各种自由运动状态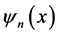 的叠加,这意味着,建在本征态上的坐标系是惯性系。本征态同时并存,表明波函数叠加态中对应一个平行并存的惯性系群的同时存在。对波函数
的叠加,这意味着,建在本征态上的坐标系是惯性系。本征态同时并存,表明波函数叠加态中对应一个平行并存的惯性系群的同时存在。对波函数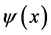 进行络伦兹变换,相当于对一个平行的惯性系群中的本征态的同时变换。
进行络伦兹变换,相当于对一个平行的惯性系群中的本征态的同时变换。
对应于波函数定态,处在本征态中的微观客体作自由运动,反过来,本征态(平面波)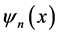 的叠加,将构成一个波包,对应一个自由运动的微观客体。物质波是物理波,能级间物质波的相干性也有了物理学基础,消除了概率波不能相干的认识障碍。能级间的量子跃迁可看作微观客体运动速度的跃迁[3] ,这类似坐标变换中两个不同匀速运动惯性系间的跃迁转换。
的叠加,将构成一个波包,对应一个自由运动的微观客体。物质波是物理波,能级间物质波的相干性也有了物理学基础,消除了概率波不能相干的认识障碍。能级间的量子跃迁可看作微观客体运动速度的跃迁[3] ,这类似坐标变换中两个不同匀速运动惯性系间的跃迁转换。
本征态之间连续作用的动力学演变过程被量子化截断、删除(忽略),保留非连续的“局部匀速运动”状态,本征态之间的变更,相当于本征态惯性系之间的变更;本征态之间的“突变”性及本征态叠加,使自由微观客体“同时”处在“不同本征态”的对应惯性系中,且运动规律具有洛伦兹有不变性。这是量子力学微观客体的运动学特征。所以说量子力学定态薛定谔方程是运动学方程[8] 。
4. 量子力学中的非惯性系分析
4.1. 相对论中的惯性系与非惯性系
狭义相对论中,坐标变换从一个惯性系到另一个惯性系不涉及坐标系间的速度渐变过程——即连续相互作用过程。惯性系的变更是“突变”的,而且可“同时”进行任意惯性系间的坐标变换。力学方程的形式在惯性系间的坐标变换中具有洛伦兹不变性。
相对论中,微观客体的理论模型是质点,是点粒子。粒子的能量、动量不是量子化的,相互作用及运动状态不被量子分割、截断,而依然是连续的,其状态变更也是连续的,有时间排序,同一微观客体的“不同状态”,不可能“同时”出现。但根据相对性原理,微观客体的力学运动规律(状态),在不同惯性系坐标变换中,均可保持洛伦兹不变性。
相对论中,坐标变换若考虑坐标系间速度的渐变过程,就会有惯性力(等效引力)出现,时空将发生弯曲,是非惯性系,洛伦兹变换失去协变性。所以,人们常说狭义相对论是不考虑引力的力学体系。
4.2. 量子力学中的惯性系与非惯性系
上一节,我们讨论了量子力学中的惯性系。量子力学实质是把连续作用和连续运动的物理过程,根据新的实验实事,通过量子化分割变成间断作用和间断匀速运动(波动)的物理学。现在我们考虑消去量子力学能级间能量、动量量子化。这等于恢复了微观客体宏观非量子化的连续作用力(连续场作用)。这样,一方面,本征态之间的“间断、突变”性及本征态的同时并存随之消失,物理上失去了自身的独立自相干波源,自相干性随之消失。这是宏观物体不能自相干的物理原因。另一方面,能量、动量量子化的消失和连续作用力的重新恢复,微观客体也将由间断的非点粒子自由运动波的叠加态,还原成整体的点粒子连续加速运动状态,与微观客体联系的各个本征态惯性系变成非惯性系,惯性力(或等效引力)也将出现,空间变得不均匀,洛伦兹协变性失效。
量子力学与相对论在惯性系间消去各自的“突变”性上有了相似性,都需要恢复(提供)外加的连续作用力。洛伦兹协变的量子力学可称作为狭义相对论量子力学。
必须指出,在考虑状态波函数的时间演化时,微观客体由间断的匀速运动的叠加变成连续的加速运动,不能与量子力学中的薛定谔绘景或海森伯绘景等同。尽管两者都有外场介入,但前者伴随“态的时间演变”中能量、动量量子化的消失,有连续作用力的出现;后者则伴随“态的时间演变”中能量子的失放和吸收,有非连续作用力(球量子)的出现。显然,后者的物理过程仍然是量子力学的,适合希尔伯特空间数学方法。
从量子力学微观客体“同时”处在不同本征态的叠加,到狭义相对论不同惯性系“同时”对应微观客体某一宏观连续力学状态的转变,它涉及消除物理过程的量子化分割,以及微观双4维时空向宏观4维实时空,场物质球向点粒子,物质波向概率波,微观非连续性作用向宏观连续性作用的转换。微观的非连续性本征态已经包含在宏观连续力学状态之中。量子测量很可能就是微观的非连续性本征态向宏观某一对应连续力学状态寻求瞬间共振显示的或然性过程。量子态的坍缩,是量子测量中两个空间(复-实时空)的“突变”转换,就像惯性系坐标变换中坐标系的“突变”一样。这只是一个认知过程,是对实际测量过程的理论简化。
将上述分析引进量子场论,我们将清楚地看到规范变换中引进协变导数的物理本质,看到狭义相对论量子力学与广义相对论量子力学之间的内在联系。
5. 杨-米尔斯规范场及其规范变换物理意义再分析
规范场论是标准模型的基石。希格斯粒子的发现,标准模型获得的巨大成功,让全世界物理学家欢呼声一片。但人们不要忘记,规范场论中,波函数一开始就赋予了概率解读,物质波 是概率波[9] 。规范场论中的规范变换是对概率函数的数学操作,引进的规范场
是概率波[9] 。规范场论中的规范变换是对概率函数的数学操作,引进的规范场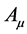 是电磁场的矢势,其原初也只有数学意义。规范变换给人更多的印象是数学意义上的规范不变性,物理意义展示不够。理论中的波函数是个“稻草人”。双4维时空中的物质波是物理波,真实还原了波函数实在论女儿身,揭示了规范变换的真实物理意义。
是电磁场的矢势,其原初也只有数学意义。规范变换给人更多的印象是数学意义上的规范不变性,物理意义展示不够。理论中的波函数是个“稻草人”。双4维时空中的物质波是物理波,真实还原了波函数实在论女儿身,揭示了规范变换的真实物理意义。
5.1. 整体规范变换
对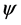 、
、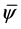 和
和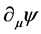 做整体规范变换[9] ,
做整体规范变换[9] , 常数,
常数,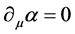 ,有
,有
 (1)
(1)
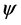 、
、 、
、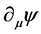 按相同规律变换,规范不变性成立。构造自由场的拉格朗日密度,代入拉格朗日方程,即可得到洛伦兹协变形式的狄拉克方程
按相同规律变换,规范不变性成立。构造自由场的拉格朗日密度,代入拉格朗日方程,即可得到洛伦兹协变形式的狄拉克方程
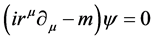 (2)
(2)
狄拉克方程的解 ,赋予了概率解读,杨—米尔斯规范场中,波函数
,赋予了概率解读,杨—米尔斯规范场中,波函数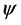 不是实在论的,无法分析波函数相位因子的物理意义,相因子物理意义不明确。
不是实在论的,无法分析波函数相位因子的物理意义,相因子物理意义不明确。
5.2. 局域规范变换
式(1)中,若 ,即所乘相位因子是时空坐标
,即所乘相位因子是时空坐标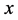 的函数。对带电自由微观客体的场量
的函数。对带电自由微观客体的场量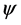 及其导数
及其导数 做局域规范变换[9] :
做局域规范变换[9] :
 (3-1)
(3-1)
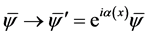 (3-2)
(3-2)
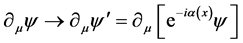
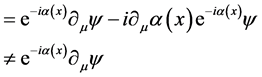 (3-3)
(3-3)
传统分析认为,原因在于式(3-3)增加了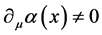 项,场量与场量导数的变换不一致,多出现了空间梯度项,空间不均匀。用式(3)构造拉格朗日密度,代入拉格朗日方程,不能得到洛仑兹协变的狄拉克方程。数学上,通过协变导数
项,场量与场量导数的变换不一致,多出现了空间梯度项,空间不均匀。用式(3)构造拉格朗日密度,代入拉格朗日方程,不能得到洛仑兹协变的狄拉克方程。数学上,通过协变导数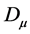
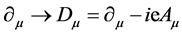 (4)
(4)
引进规范场 ,就可恢复局域规范变换规范不变性。
,就可恢复局域规范变换规范不变性。 是电磁场的矢势,其原初也只有数学意义。微观客体受的是电磁力,体现物理实在性的应是电场E。这里,为了满足数学形式的物理需要,人们不得不改变原有认识,强行赋予矢势
是电磁场的矢势,其原初也只有数学意义。微观客体受的是电磁力,体现物理实在性的应是电场E。这里,为了满足数学形式的物理需要,人们不得不改变原有认识,强行赋予矢势 以实在论物理意义。
以实在论物理意义。
当然,引入协变导数后再构造拉格朗日密度,并将总拉格朗日密度代入拉格朗日方程,即可得到形式不变的狄拉克场方程:
 (5)
(5)
从局域规范变换,我们再次看到了数学的神通和对称美。
但我们要问:即使赋予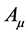 物理实在性,一个数学的概率函数如何与一个物理场发生相互作用?这是一个心结。更何况
物理实在性,一个数学的概率函数如何与一个物理场发生相互作用?这是一个心结。更何况 最初也还只有数学意义,其物理实在性是临时强行赋予的,数学函数作用于数学函数引出系列物理意义,这种一厢情愿,逻辑上行得通吗?杨振宁上世纪80年代初在武汉大学与物理学者座谈,一位学者就问及此事,据说杨振宁无言以对。
最初也还只有数学意义,其物理实在性是临时强行赋予的,数学函数作用于数学函数引出系列物理意义,这种一厢情愿,逻辑上行得通吗?杨振宁上世纪80年代初在武汉大学与物理学者座谈,一位学者就问及此事,据说杨振宁无言以对。
传统理解认为,局域规范变换中,微观客体与场的相互作用是在“引进规范场”之后实现的。引进规范场之前数学上破坏规范对称性的物理原因还有吗?数学变换造成的不对称由引进的物理场消除,数学背后一定有物理原因。物理的原因由物理来消除,数学美与物理美才能协调。什么物理原因破坏了规范对称性?这要对局域规范变换的数学操作作出物理解读。因此,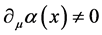 项自身,有更深层的物理原因。规范场论中相角
项自身,有更深层的物理原因。规范场论中相角 与微观客体相联系的物理意义值得思考[8] 。
与微观客体相联系的物理意义值得思考[8] 。
6. 德布罗意-薛定谔物质波(场量 )与规范变换
)与规范变换
6.1. 物质波是“旋转场物质”的波动运动
双4维时空量子力学描述中,微观客体不是几何点,是转动的场物质球。物质波不是概率波,是“旋转场物质”的波动运动[2] [3] ,是物理波。物质波
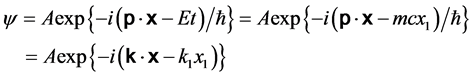 (6)
(6)
式(6)是一个平面物质波。它是一个物理波。式中,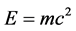 ,
,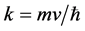 ,
,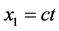
 ,
,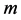 为运动质量。
为运动质量。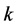 是场物质球的曲率,曲率坐标是质点模型隐藏的空间自由度,与微观客体物质密度正相关,物质波的相位与微观客体自身结构有了联系。物质波将微观客体的物质性与自身时空结构融为一体。
是场物质球的曲率,曲率坐标是质点模型隐藏的空间自由度,与微观客体物质密度正相关,物质波的相位与微观客体自身结构有了联系。物质波将微观客体的物质性与自身时空结构融为一体。
6.2. 自由微观客体物质波规范变换的物理实质
6.2.1. 自由微观客体物质波初相的物理意义
波函数描述物质波,是物理波,不是数学的几率函数,但物理波与概率波可以相互映射。物质波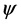 的相位有其特定的物理意义[6] 。
的相位有其特定的物理意义[6] 。
自由微观客体物质波式(6)中,其相位是微观客体离开原点 时开始记录的。初始条件是
时开始记录的。初始条件是 ,
, ,物质波初始相位
,物质波初始相位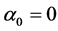 。要使被描述的物质波的初相不为零,可在
。要使被描述的物质波的初相不为零,可在 ,
,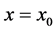 点开始记录。设被记录的物质波为
点开始记录。设被记录的物质波为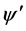 ,则物质波式(6)中的位置变量
,则物质波式(6)中的位置变量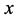 应为
应为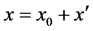
于是式(6)变为
 (7)
(7)
这里,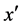 仍是
仍是 轴上的时空标度。令
轴上的时空标度。令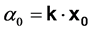 ,将
,将 用
用 标记,式(7)变为
标记,式(7)变为
 (8)
(8)
式(8)为初相不为零的自由微观客体物质波波函数。初相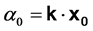 ,包含微观客体特定的形态结构
,包含微观客体特定的形态结构 ,即运动速度因子
,即运动速度因子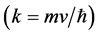
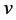 ,因此,波函数初相有物理含义。与式(6)描述的物质波相比,它只是在同一
,因此,波函数初相有物理含义。与式(6)描述的物质波相比,它只是在同一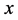 轴上,把描述同一物质波运动的空间坐标往后平移了一段距离
轴上,把描述同一物质波运动的空间坐标往后平移了一段距离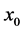 ,数学上是坐标平移,物理上类似交流电初始相位中转子的初始方位。自由微观客体物质波
,数学上是坐标平移,物理上类似交流电初始相位中转子的初始方位。自由微观客体物质波 的相位变化除依赖于微观客体的运动速度
的相位变化除依赖于微观客体的运动速度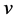 (坐标系K′的速度)或微观客体特定的形态结构——曲率
(坐标系K′的速度)或微观客体特定的形态结构——曲率 外,还与记录的初始位置坐标
外,还与记录的初始位置坐标 相关。
相关。
物质波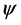 、
、 描述的显然是同一参照系中微观客体同一波动状态。但记录物质波的空间初始坐标不同,初相不同,
描述的显然是同一参照系中微观客体同一波动状态。但记录物质波的空间初始坐标不同,初相不同,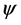 、
、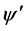 描述的是自由微观客体的同一运动状态,符合规范不变性形式要求。结合场物质球模型,我们看到了费曼路径积分中不同路径波函数概率相同、初相不同,以及如何回到宏观路径的物理原因和过程[10] 。
描述的是自由微观客体的同一运动状态,符合规范不变性形式要求。结合场物质球模型,我们看到了费曼路径积分中不同路径波函数概率相同、初相不同,以及如何回到宏观路径的物理原因和过程[10] 。
6.2.2. 自由微观客体物质波的整体规范变换
我们把自由微观客体物质波波函数式(6)与式(8)写成指数函数形式:
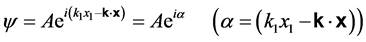
令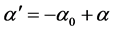 ,所以
,所以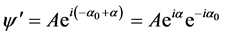
故
 (9)
(9)
式(9)中,初始相位 常数,它具有阿贝尔和非阿贝尔整体规范变换形式。所乘相因子
常数,它具有阿贝尔和非阿贝尔整体规范变换形式。所乘相因子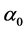 有特定的物理含义:
有特定的物理含义: 常数,
常数, 不变,
不变, 常数,运动速度
常数,运动速度 常数
常数 ,是自由微观客体,不受力,做匀速运动,且记录物质波相位的初始位置
,是自由微观客体,不受力,做匀速运动,且记录物质波相位的初始位置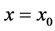 ,建在微观客体上的坐标系是惯性系。
,建在微观客体上的坐标系是惯性系。
自由微观客体物质波整体规范变换是物质波的坐标平移。微观客体的受力状况不变,运动状态不变,形态结构不变,这正是规范变换中整体规范变换的物理和数学要求[8] 。
在双4维时空量子力学描述中,波函数 是物理波,描述微观客体的波动存在形态,其相位包含微观客体的速度信息、几何结构信息,物质密度信息,有明确的物理意义。
是物理波,描述微观客体的波动存在形态,其相位包含微观客体的速度信息、几何结构信息,物质密度信息,有明确的物理意义。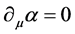 ,即为
,即为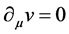 ,微观客体作匀速运动,有流和荷的守恒。建在微观客体上的坐标系K′时空均匀、平直,是惯性系,保证了双4维时空实、虚空间的均匀、平直性,
,微观客体作匀速运动,有流和荷的守恒。建在微观客体上的坐标系K′时空均匀、平直,是惯性系,保证了双4维时空实、虚空间的均匀、平直性, 具有洛伦兹协变性。带电自由微观客体受力状况不变,运动状态不变,微观客体形态结构不变,整体规范变换有了规范不变性。如果再加上量子态的突变性,本征态的叠加,并引进希尔伯特空间,双4维时空对量子力学描述就几乎趋于完美。整体规范变换既有数学美,更有数学美的物理学基础。
具有洛伦兹协变性。带电自由微观客体受力状况不变,运动状态不变,微观客体形态结构不变,整体规范变换有了规范不变性。如果再加上量子态的突变性,本征态的叠加,并引进希尔伯特空间,双4维时空对量子力学描述就几乎趋于完美。整体规范变换既有数学美,更有数学美的物理学基础。
6.2.3. 物质波的局域规范变换
初相
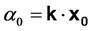 (10)
(10)
中,如果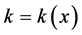 ,也即
,也即 ,
, 、
、 是时空点的函数,微观客体作变速运动,其形状也在变。微观客体受到了连续力的作用。
是时空点的函数,微观客体作变速运动,其形状也在变。微观客体受到了连续力的作用。 表明,只要对物质波做局域规范变换,微观客体已处在连续力场之中。将
表明,只要对物质波做局域规范变换,微观客体已处在连续力场之中。将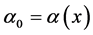 代入式(9)有
代入式(9)有
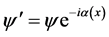 (11)
(11)
式(11)具有阿贝尔和非阿贝尔局域规范变换形式。对自由微观客体物质波做局域规范变换,微观客体就已置于力场之中。自由微观客体受力状况发生了变化,运动状态发生了变化,其形体结构也发生了变化。建在微观客体上的坐标系K′已不是惯性系,是非惯性系。空间均匀、平直性遭破坏,时空发生了弯曲,与本征态联系的惯性系也随之变成非惯性系。惯性系的消失,填补了突变本征态之间的连续作用过程,体现了微观客体与场之间的连续相互作用。式(11)是微观客体自身非惯性系的时空特征与场物质球波动特征相联系的表达式,已不是平面波。连续相互作用和非惯性系的出现,空间梯度产生,式(11)不再满足洛伦兹不变性,是自由微观客体从整体规范变换过渡到局域规范变换,规范不变性遭破坏的物理原因[8] 。所以:
1)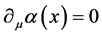 ,有
,有 ,带电微观客体作匀速运动,式(3)中(c)式第二项消失,这就是带电自由微观客体整体规范变换。
,带电微观客体作匀速运动,式(3)中(c)式第二项消失,这就是带电自由微观客体整体规范变换。
2)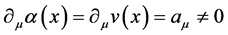 ,带电微观客体有加速度,受到连续电场力作用,规范场完全成了破坏规范不变性的祸首。
,带电微观客体有加速度,受到连续电场力作用,规范场完全成了破坏规范不变性的祸首。
3) ,表明微观客体自身坐标系空间梯度的存在,引进
,表明微观客体自身坐标系空间梯度的存在,引进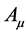 正好能消除这一空间梯度,
正好能消除这一空间梯度, 有了空间结构赋义,摆脱了纯数学意义的原始内涵。
有了空间结构赋义,摆脱了纯数学意义的原始内涵。
引入协变导数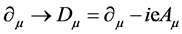 ,是为消去微观客体与场之间的连续相互作用,恢复能量、动量量子化分割,及微观客体的自由运动状态,恢复微观客体自身坐标系K′的惯性系地位,使“突变本征态”叠加态得到还原,量子力学回到原有的理论框架。将构造的总拉格朗日密度代入拉格朗日方程,就可得到形式不变的狄拉克场方程:
,是为消去微观客体与场之间的连续相互作用,恢复能量、动量量子化分割,及微观客体的自由运动状态,恢复微观客体自身坐标系K′的惯性系地位,使“突变本征态”叠加态得到还原,量子力学回到原有的理论框架。将构造的总拉格朗日密度代入拉格朗日方程,就可得到形式不变的狄拉克场方程:
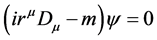 (12)
(12)
这里,我们既看到了数学的神通和对称美,也看到了物理美。
规范场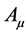 具有空间结构赋义,正是因为如此,相对论量子力学中才能够把电磁场4维矢势
具有空间结构赋义,正是因为如此,相对论量子力学中才能够把电磁场4维矢势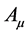 与光子波函数(由k表征的空间结构函数)等同看待[1] 。光子是通过4维矢势
与光子波函数(由k表征的空间结构函数)等同看待[1] 。光子是通过4维矢势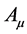 的结构内涵建构的。光子的自旋为1,光波相对于运动方向场量转过
的结构内涵建构的。光子的自旋为1,光波相对于运动方向场量转过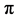 角改变方向,转过
角改变方向,转过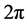 回到原位。光子是个球状结构。引力子的自旋为2 [11] ,引力波(旋转的引力子)相对于运动方向场量转过
回到原位。光子是个球状结构。引力子的自旋为2 [11] ,引力波(旋转的引力子)相对于运动方向场量转过 即改变方向,转过
即改变方向,转过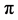 回到原位,引力子的空间结构应类似于椭球[12] 。
回到原位,引力子的空间结构应类似于椭球[12] 。
物理系统的对称性及拉格朗日密度不变性揭示守恒流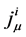 和守恒荷
和守恒荷 的物理本质:流和荷的守恒刚好对应载荷微观客体匀速运动,坐标系K′的空间均匀、平直性;局域规范变换规范不变性的破坏,意味着流、荷守恒的破坏,即微观客体匀速运动状态的破坏,K′空间均匀、平直性的破坏。规范场的引入,尽管体现了带电微观客体与电磁场的作用,但那是一种抵消作用,使总作用力为零,恢复微观客体受力状况、结构形态和自由运动状态不变,及坐标系K′空间均匀、平直性不变,从而保证规范不变性。过去人们对这一物理机制似乎认识不足,忽视了在对波函数
的物理本质:流和荷的守恒刚好对应载荷微观客体匀速运动,坐标系K′的空间均匀、平直性;局域规范变换规范不变性的破坏,意味着流、荷守恒的破坏,即微观客体匀速运动状态的破坏,K′空间均匀、平直性的破坏。规范场的引入,尽管体现了带电微观客体与电磁场的作用,但那是一种抵消作用,使总作用力为零,恢复微观客体受力状况、结构形态和自由运动状态不变,及坐标系K′空间均匀、平直性不变,从而保证规范不变性。过去人们对这一物理机制似乎认识不足,忽视了在对波函数 作局域规范变换时就引进了带电微观客体与场的相互作用,误认为带电微观客体与场的相互作用只是在引进规范场时才发生。认识上的这种本末倒置,为规范变换引进引力场设置了障碍。它与力是产生速度的原因还是产生加速度的原因,其错误有些类似,阻碍了物理学的进一步顺利发展。
作局域规范变换时就引进了带电微观客体与场的相互作用,误认为带电微观客体与场的相互作用只是在引进规范场时才发生。认识上的这种本末倒置,为规范变换引进引力场设置了障碍。它与力是产生速度的原因还是产生加速度的原因,其错误有些类似,阻碍了物理学的进一步顺利发展。
量子色动力学也有类似的情形。将电子换成夸克,电磁场换成胶子场,数学上要用到群论,考虑到夸克场波函数的物质实在性及其相位的物理意义,量子色动力学完全可以做出相同的动力学分析[8] [9] 。
7. 引力场与规范变换的讨论
物质间所有基本相互作用力均是规范力,已成为当今物理学家的信念。近半个世纪已来,人们对引力规范理论进行了大量的研究,做了许多工作,取得了不少成果,然而其数学结构越来越复杂,物理图象却越来越模糊,远没有内部对称规范理论那么成熟。已故物理学家王仁川认为,其原因可能是引力不是规范力,宏观世界里的时空弯曲在微观世界可以忽略不计。如果引力可以纳入规范力框架内,就必须让宏观的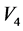 黎曼弯曲空间推广到
黎曼弯曲空间推广到 嘉当活动标架空间,这将引来自由质点运动的测地线不是最短程线,而违反公理性的传统经验。微观客体不是质点而是物质波,自旋与挠率场相互作用可理解为使其偏离最短短程线的理由,而宏观的质点找不到这类理由。人们可以设想让度规场与规范场完全脱勾,度规场被看成特殊形式的物质场,爱因斯坦场方程的形式不变,只是物质场的能动张量部分,增加了时空洛伦兹对称的规范场的能动张量。爱因斯坦场方程决定度规场,规范场决定嘉当联络,微观
嘉当活动标架空间,这将引来自由质点运动的测地线不是最短程线,而违反公理性的传统经验。微观客体不是质点而是物质波,自旋与挠率场相互作用可理解为使其偏离最短短程线的理由,而宏观的质点找不到这类理由。人们可以设想让度规场与规范场完全脱勾,度规场被看成特殊形式的物质场,爱因斯坦场方程的形式不变,只是物质场的能动张量部分,增加了时空洛伦兹对称的规范场的能动张量。爱因斯坦场方程决定度规场,规范场决定嘉当联络,微观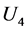 空间弯曲不能忽略。推广到宏观,微观
空间弯曲不能忽略。推广到宏观,微观 嘉当空间仍可回到宏观
嘉当空间仍可回到宏观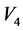 黎曼空间。这是引力规范理论研究现状[13] [14] 。
黎曼空间。这是引力规范理论研究现状[13] [14] 。
7.1. 微观世界引力规范理论及爱因斯坦场方程回顾
引力规范理论中,微观世界爱因斯坦场方程,其总拉氏量为[13]
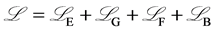 (13)
(13)
其中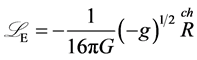 为爱因斯坦度规场;
为爱因斯坦度规场;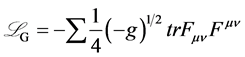 代表规范场,∑是对规范场求和;
代表规范场,∑是对规范场求和; 代表费米子场;
代表费米子场; 代表矢量玻色子场,
代表矢量玻色子场,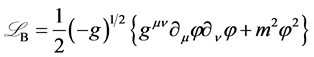 代表标量玻色子场。
代表标量玻色子场。
总作用量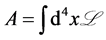 对度规
对度规 变分,得到微观领域
变分,得到微观领域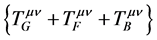 爱因斯坦场方程
爱因斯坦场方程
 (14)
(14)
其中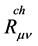 表示仅用
表示仅用 空间度规
空间度规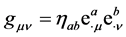 构造的曲率,称为爱因斯坦曲率。由于引力常数
构造的曲率,称为爱因斯坦曲率。由于引力常数 的值非常小,在微观范围内,规范场的能动张量
的值非常小,在微观范围内,规范场的能动张量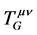 ,费米子场能动张量
,费米子场能动张量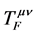 ,矢量玻色子场能动张量
,矢量玻色子场能动张量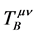 (标量玻色子场能动张量
(标量玻色子场能动张量 ),对微观范围内时空弯曲的贡献非常小。当然,宇宙产生初期或高密度引力场除外。受微观爱因斯坦场方程启发,爱因斯坦场方程应推广为
),对微观范围内时空弯曲的贡献非常小。当然,宇宙产生初期或高密度引力场除外。受微观爱因斯坦场方程启发,爱因斯坦场方程应推广为
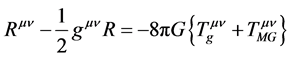 (15)
(15)
 为度规场
为度规场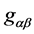 自身的能动张量,
自身的能动张量, 为物质场和规范场的能动张量。
为物质场和规范场的能动张量。 造成的时空弯曲是微观的,对宏观时空弯曲的贡献完全可以忽略。爱因斯坦真空场方程应推广为
造成的时空弯曲是微观的,对宏观时空弯曲的贡献完全可以忽略。爱因斯坦真空场方程应推广为
 (16)
(16)
7.2. 引力规范理论图象新设想
将能动张量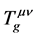 、
、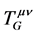 、
、 、
、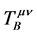 与旋转场物质球模型联系,用能动张量定义微观客体自身的曲率张量,考虑到双4维时空量子力学描述及对规范变换物理实质的新理解,对引力规范理论的建立,我们尝试提供一个图象清晰的新思路。
与旋转场物质球模型联系,用能动张量定义微观客体自身的曲率张量,考虑到双4维时空量子力学描述及对规范变换物理实质的新理解,对引力规范理论的建立,我们尝试提供一个图象清晰的新思路。
1) 研究对象:中性微观客体(比如中子——费米子)物质波规范变换。
2) 整体规范变:中性自由微观客体物质波整体规范变换与带荷自由微观客体没有什么区别。有 ,
,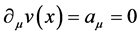 ,保证了微观客体自由运动状态不变。
,保证了微观客体自由运动状态不变。
3) 局域规范变换:中性自由微观客体物质波从整体规范变换过渡到局域规范变换,规范不变性遭破坏,出现 项,如果物理原因是引力场,则中性微观客体在引力场中运动(比如自由下落)。
项,如果物理原因是引力场,则中性微观客体在引力场中运动(比如自由下落)。
我们已经指出,量子力学实质是把连续作用和连续运动的物理过程,通过量子化分割变成间断作用和间断匀速运动(波动)的物理学。对高密度强引力场进行量子化操作,现在,
1) 首先我们假设,引力场由引力子构成,引力场被量子化。引力场中运动的微观客体产生能级跃迁,吸收或失放引力子。引力子是“椭球”,自旋为2。微观客体的运动状态被分割,出现间断本征态。本征态(平面波)的叠加态
 (17)
(17)
是引力场中的定态波函数,局部时空中微观客体作自由运动,对应惯性系或惯性系群,具有洛伦兹协变性,有整体规范不变性。
2) 引力质量与惯性质量相等,局部时空中,惯性力场与引力场等效。
对中性自由微观客体物质波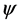 做局域规范变换,实际已假设将微观客体放进了高密度引力场。微观客体在引力场中做加速运动,其自身坐标系K’是加速系,时空发生弯曲,时空不均匀,体系失去洛伦兹协变性。通过协变导数
做局域规范变换,实际已假设将微观客体放进了高密度引力场。微观客体在引力场中做加速运动,其自身坐标系K’是加速系,时空发生弯曲,时空不均匀,体系失去洛伦兹协变性。通过协变导数 引进反向引力场
引进反向引力场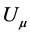 (“补偿场”),抵消局域规范变换引进的引力场,实现局部时空平直性,微观客体恢复到自由运动状态和定态波函数形式,规范不变性再次成立。它是7.1节
(“补偿场”),抵消局域规范变换引进的引力场,实现局部时空平直性,微观客体恢复到自由运动状态和定态波函数形式,规范不变性再次成立。它是7.1节 空间引进规范场实现洛伦兹协变的物理本质。
空间引进规范场实现洛伦兹协变的物理本质。
3) 引力场中的狄拉克——爱因斯坦方程
引力规范理论中,规范场是引力场 (惯性力场),通过协变导数,建构中子——费米子场
(惯性力场),通过协变导数,建构中子——费米子场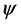 规范不变的拉格朗日密度,期待有如下形式:
规范不变的拉格朗日密度,期待有如下形式:
 (18)
(18)
 是中性自由微观客体物质波。其中,
是中性自由微观客体物质波。其中,
 (19)
(19)
由此,可导出局部时空自由微观客体狄拉克—爱因斯坦方程:
 (20)
(20)
它等效于 空间费米子(质点)满足的方程[13]
空间费米子(质点)满足的方程[13]
 (21)
(21)
方程(21)应该是将微观客体自身的几何特性变换到背景时空流形M——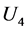 几何特性的方程。如果不考虑自旋,得到的将应是自由微观客体的克莱茵-戈登方程。
几何特性的方程。如果不考虑自旋,得到的将应是自由微观客体的克莱茵-戈登方程。
必须注意:
1) 双4维时空中微观客体不再是质点,而是场物质球,隐藏的空间自由度——曲率坐标k得到显示。场物质球的旋转与运动产生物质波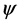 ,能量、动量均可量子化。引力场将以引力子能量量子化进行分割。
,能量、动量均可量子化。引力场将以引力子能量量子化进行分割。
2) 自由微观客体物质波整体规范变换有洛伦兹协变性,微观客体做匀速运动,自身坐标系K’是惯性系,与狭义相对论对应。能量量子化的微观客体从静止跃迁到匀速运动,坐标变换中曲率半径
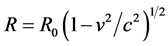 (22)
(22)
半径的变化是量子化的。物质波波频
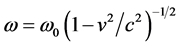 (23)
(23)
式中,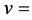 常量,曲率半径
常量,曲率半径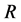 (波长)在坐标变换中全空间统一收缩,波频
(波长)在坐标变换中全空间统一收缩,波频 全空间统一增高。
全空间统一增高。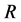 、
、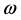 均与位置无关。物质波物质密度增加,且全空间均匀分布,是平面物质波。
均与位置无关。物质波物质密度增加,且全空间均匀分布,是平面物质波。
3) 自由微观客体做局域规范变换,微观客体做加速运动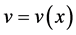 ,自身坐标系K’是加速系,时空发生弯曲,与广义相对论对应,洛伦兹协变性失效。微观客体运动速度
,自身坐标系K’是加速系,时空发生弯曲,与广义相对论对应,洛伦兹协变性失效。微观客体运动速度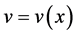 ,物质波波频
,物质波波频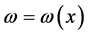 、曲率半径
、曲率半径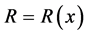 是时空点的函数。物质波物质宻度随时空点变化,非均匀分布[15] ,不是平面波。
是时空点的函数。物质波物质宻度随时空点变化,非均匀分布[15] ,不是平面波。
4) 自由微观客体做局域规范变换,微观客体已置于相互作用场中。若自由微观客体带电,通过协变导数引进的是反向电磁场;中性微观客体不带电,引进的就是反向引力场。但都是为了重新恢复量子化分割,消除 项,达到时空均匀、平直,实现规范不变性。
项,达到时空均匀、平直,实现规范不变性。
上述情形中,中性自由微观客体构成了爱因斯坦的升降机。爱因斯坦建立引力场理论的思想方法,与规范场的思维方法得到统一。
7.3. 引力规范理论新设想与爱因斯坦引力理论的内在联系
爱因斯坦引力理论用的是质点模型,而我们的引力规范理论用的是场物质球模型,物质波是物理波,两者之间必须有一个转换。
如果让场物质球模型还原成质点模型,那么,引力场中运动微观客体的波动描述,在质点还原中,象对狭义相对论的分析一样,其自身动力学特性及自身的时空特征(由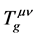 、
、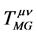 产生的几何特征,在宏观环境下
产生的几何特征,在宏观环境下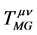 的影响可以忽略不计),将还原成描述其运动的坐标系的时空属性,且与时空点相关。而微观客体还原成了自由运动的质点,描述其运动的坐标系的时空却发生了弯曲。这正是“物质告诉时空如何弯曲,时空告诉物质如何运动”的物理展现[15] 。弯曲空间自由质点的运动方程就是广义相对论中的“测地线方程”。
的影响可以忽略不计),将还原成描述其运动的坐标系的时空属性,且与时空点相关。而微观客体还原成了自由运动的质点,描述其运动的坐标系的时空却发生了弯曲。这正是“物质告诉时空如何弯曲,时空告诉物质如何运动”的物理展现[15] 。弯曲空间自由质点的运动方程就是广义相对论中的“测地线方程”。
 (24)
(24)
其中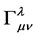 是仿射联络。
是仿射联络。
从物质波的认知及场物质球模型到点模型的转换,似乎让人悟出了广义相对论引力场方程中,时空曲率与物质的能动张量相等的物理本质。爱因斯坦的引力场方程:
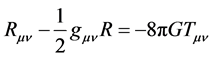 (25)
(25)
考虑 、
、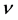 指标缩并,
指标缩并, ,得到
,得到
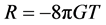 (26)
(26)
背景空间的标量曲率,与决定引力源自身空间结构的能动标量有关,它是将引力源自身的空间结构作质点抽象时转换过去的。爱因斯坦的引力场方程有了坚实的物理学基础,不是“泥巴揑的”。
在双4维时空量子力学描述中,物质波式(6)是洛伦兹协变的,微观客体的运动速度不可能超光速。因此,微观客体的质量不可能无穷大,物质波的频率也不可能无穷大,波长(曲率半径)不可能为零,曲率k不可能无穷大,我们认为应截止在普朗克长度 。微观客体终究不是点,物质密度分布因而不可能无穷大,没有引力场中的奇点出现[15] 。在
。微观客体终究不是点,物质密度分布因而不可能无穷大,没有引力场中的奇点出现[15] 。在 的范围以下,微观客体“点”描述、“弦”描述、“圈”描述、“球”描述均失效。那里是一片混沌世界。上帝还没有交给人类认知的钥匙。
的范围以下,微观客体“点”描述、“弦”描述、“圈”描述、“球”描述均失效。那里是一片混沌世界。上帝还没有交给人类认知的钥匙。
我们假定,广义相对论高密度引力场的能量量子化由引力子的能量分割实现,有显著能级区分,存在能级跃迁,吸收和失放引力子,量子化的非点微观客体在各能级做自由运动,对应的时空微元是平直的。对应于普朗克长度 以上的高密度场物质球,微观客体以物质波动形态出现,构成本征态的叠加态,方程是线性的。
以上的高密度场物质球,微观客体以物质波动形态出现,构成本征态的叠加态,方程是线性的。
爱因斯坦的引力场方程,是球模型转向点模型,微观非连续作用转向宏观连续作用,微观局部平直性时空转向宏观弯曲时空,自由运动转向加速运动的场方程,因而微观量子化的线性方程也就转变成了宏观点粒子的非线性方程。
8. 结论与讨论
1) 本征态的叠加,实际是通过能量、动量量子化将一个连续作用或连续运动状态分解成分立运动状态(几何上对应线元或面元),每一个分立的状态就是量子力学中的本征态。能量、动量量子化及本征态的出现,正是局部平直时空惯性系的生存基础。物理学为数学提供了丰富的演译舞台。
2) 电磁场、引力场的量子化,本质上是截断、消除连续作用场的操作方法,将一个场中连续的加速运动分解为非连续的自由运动。微观客体的自由运动是量子力学定态波函数叠加原理的物理本质。反过来,能量、动量量子化的消除,又将导致连续作用场的重新引入,加速运动状态的出现。这就是广义相对论与量子力学物理上内在的本质联系。
3) 如果狭义相对论的建立包含将运动物体自身的时空特征,转化为建在其上坐标系的时空属性,而物体自身则抽象成质点的过程;那么,在微观领域,建构场物质球及由转动场物质球推导德布罗意-薛定谔物质波表述形式的过程,则是将转化到坐标系的时空属性,还原为运动物体自身时空结构的逆过程。隐藏的空间自由度(放在复数时空的虚部)得到显示。而这个还原了的时空结构——物质波是洛伦兹协变的。
4) 微观客体不是“质点”[16] [17] ,有隐藏空间自由度,物质波是物质场的波动存在形态,是物理波。波函数的振幅和相位包含有微观客体的速度信息、几何结构信息,物质密度信息,有特定的物理含义。在波函数整体规范变换与局域规范变换中,如果忘记它的特定物理含义,很可能会在抽象的数学演算游戏中迷失方向,并引来物理上的不协调和理解上的歧义。
5) 中性自由微观客体从整体规范变换过渡到局域规范变换,通过协变导数引进规范场,实现规范不变性,恢复洛伦兹协变性,与黎曼度规变换成局部时空中闵可夫斯基度规,恢复洛伦兹协变性类似。
6) 统一场论不能走点模型引力量子化之路,点模型引力理论不能量子化。因为,能量量子化的同时包含有微观客体自身几何形态的量子化。点模型与量子化概念不协调。统一量子场与引力场,采用非点模型的规范场理论方法可能是正确的选择。
致谢
感谢参与此文讨论的所有专家、学者。