1. 引言
四旋翼飞行器凭借其结构简单,能够自主起飞和着陆,能以各种姿态进行飞行,适应性强等优点而一直成为无人机方向研究的热点。但是,受其自身复杂的动力学特性和外界环境扰动的影响,四旋翼飞行器同时具有高度的非线性,强耦合性以及模型参数不确定性。因此,如何对四旋翼机器人进行准确控制,提高控制系统鲁棒性是工程师面临的挑战性问题。
目前国内外针对四旋翼飞行器的控制方法进行了大量的研究,其中,滑模变结构控制[1] 由于与系统的参数以及外部干扰无关、鲁棒性强[2] 等特点而备受关注,加之该控制算法简单,易于工程实现,已经在众多领域中得到广泛的应用。然而滑模变结构控制在本质上是不连续的,在滑动模态下会伴随着高频抖振[3] 的问题,并且很容易激发系统的未建模特性,从而影响系统的控制性能,给实际应用带来困难。
在常规的控制方法中,文献[4] 采用PID控制算法实现直线段和弧线段的轨迹跟踪,并通过在线调整控制参数消除飞行过程中的扰动。文献[5] [6] 从不同角度阐述了四旋翼机器人存在建模误差的情况下,利用自适应控制技术解决无人机的控制问题。上述控制算法虽然可以实现无人机的姿态和位置控制,但系统的鲁棒性不强。文献[7] [8] 设计了一种自适应动态逆控制器,利用反馈线性化方法构建非线性逆动力学模型来减少无人机系统的非线性特征,提高轨迹跟踪精度。文献[9] 针对四旋翼机器人飞行控制问题提出了一种反演滑模控制方法,在满足李雅普诺夫稳定条件前提下设计滑模控制律来加强控制系统的鲁棒性。文献[10] 设计了一种鲁棒自适应滑模控制器,将自适应模糊技术和滑模技术相结合来消除系统中的不良抖振。文献[11] -[13] 将自适应控制与滑模控制相结合,针对“I”型结构四旋翼机器人设计了一个自适应动态变量用于抵消系统的扰动误差,实现系统的稳定与导航控制。
本文将自适应控制与滑模变结构控制结合起来,提出了一种多输入多输出的自适应滑模变结构控制,分别应用于系统的快回路和慢回路[14] 中,有效地补偿了系统的模型不确定性和外界扰动。通过Lyapunov理论证明了该方法能够保证系统的稳定性。文中同时也介绍四旋翼机器人的动力学模型,提出自适应滑模控制方法并进行了详细分析,并通过仿真验证了方法的可行性和良好的航点轨迹跟踪性能。
2. 四旋翼飞行器动力学模型
假设在惯性空间里,地球表面是水平并且静止的,建立四旋翼机器人的地面坐标系和机体坐标系,如图1所示。
四旋翼机器人由四个螺旋桨提供三个轴向的合外力矩和垂直于机体的升力,其表达式如下:
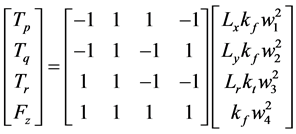 (1)
(1)
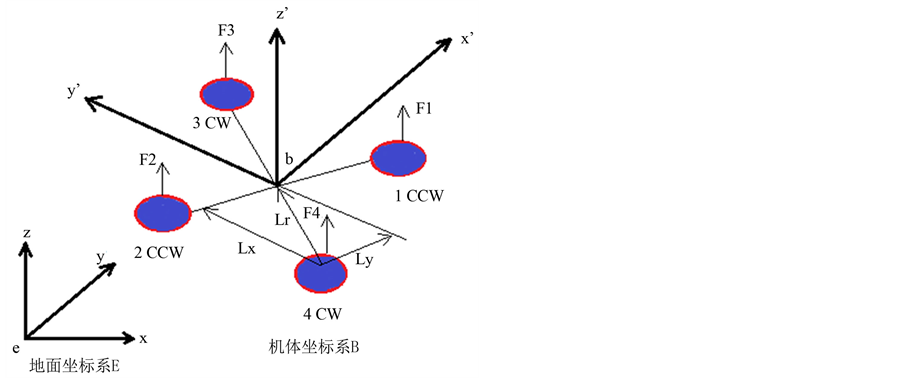
Figure 1. Flat earth frame and rigid body frame
图1. 平地坐标和机体坐标系
其中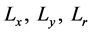 分别表示螺旋桨中心到
分别表示螺旋桨中心到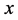 ,
,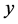 轴和原点之间的距离。
轴和原点之间的距离。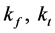 分别表示螺旋桨的升力系数和逆时针力矩系数。
分别表示螺旋桨的升力系数和逆时针力矩系数。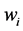 表示电机的转子速度,
表示电机的转子速度,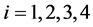 。
。
根据牛顿-欧拉的刚体动力学方程,得到四旋翼机器人的六自由度动态模型如下:
 (2)
(2)
 (3)
(3)
其中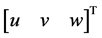 、
、 分别表示机体的线速度和角速度。
分别表示机体的线速度和角速度。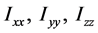 表示刚体绕三轴的转动惯量。
表示刚体绕三轴的转动惯量。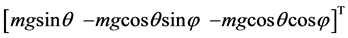 为机体的质心沿三轴的重力分量。当无飞机在地面上或者刚起飞的时候会受到地面弹力的影响,而当离开地面飞行的时候弹力就会消失,表示为
为机体的质心沿三轴的重力分量。当无飞机在地面上或者刚起飞的时候会受到地面弹力的影响,而当离开地面飞行的时候弹力就会消失,表示为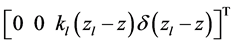 ,其中
,其中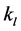 、
、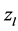 分别为弹性系数和地面弹性变形量,并且函数
分别为弹性系数和地面弹性变形量,并且函数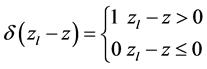 。
。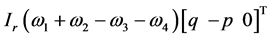 表示螺旋桨的陀螺力矩向量。
表示螺旋桨的陀螺力矩向量。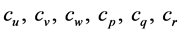 分别表示气动力和气动力矩系数。
分别表示气动力和气动力矩系数。
将四旋翼机器人进行坐标转换,可得到地面坐标系下的角速度和速度方程如下:
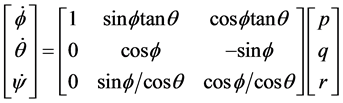 (4)
(4)
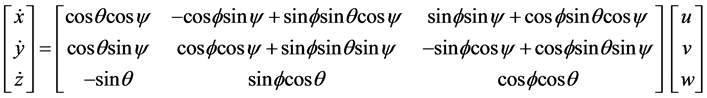 (5)
(5)
其中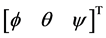 代表机体在地面坐标系下的滚转角、俯仰角和偏航角,
代表机体在地面坐标系下的滚转角、俯仰角和偏航角,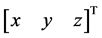 代表机体在地面坐标系下的位置。
代表机体在地面坐标系下的位置。
由于螺旋桨的转速跟直流无刷电机的输入电压成正比,因此通过电机控制单元输出脉宽调制信号来调节输入电压的大小,进而控制电机的转速。在姿态控制系统中,必须要考虑电机的数学模型,如下所示:
 (6)
(6)
其中 ,
,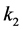 ,
, 为电机模型中的常量,
为电机模型中的常量, 电机系统的输入调节量。
电机系统的输入调节量。
以上为四旋翼机器人的动力学、导航和电机模型方程,包含16个状态变量和4个控制量,从中可以看出其固有的欠驱动性和强耦合性特征。
3. 自适应反步滑模控制系统设计
设计姿态控制器,使系统的飞行轨迹能够跟踪期望值,并保持良好的动态性能。根据时标分离原则,建立了一种快慢回路的控制器结构,在每个回路中,将自适应滑模控制应用于其中,如图2所示。再根据反步法理论,将上一回路的虚拟控制律作为下一回路的跟踪目标,以此类推完成整个控制律的设计,最终获得整个闭环系统的实际控制律和自适应律,并且结合Lyapunov理论分析方法来保证闭环系统的稳定性。运用该方法设计控制器,不仅降低了设计难度,使得控制器结构简单,而且更易于该算法的实现。
3.1. 快回路自适应滑模控制
1) 快回路是四旋翼机器人姿态控制反馈回路,为飞行器提供三轴合外力矩指令,其响应频率选取50 Hz。把快回路分解为较快回路和最快回路,最快回路是角速度反馈回路,在设计过程中加入自适应滑模控制方法来补偿系统误差,提高系统鲁棒性。忽略公式(3)中陀螺力矩和阻力力矩的影响,得到:
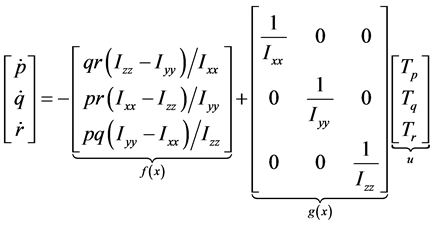 (7)
(7)
针对非线性多输入输出系统,考虑如下仿射非线性控制方程
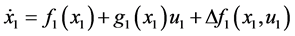 (8)
(8)
定义 ,
,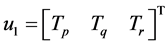 ,
,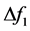 表示系统的不确定项和扰动项。假定矩阵
表示系统的不确定项和扰动项。假定矩阵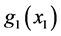 是可逆的,设计快回路的控制法则如下:
是可逆的,设计快回路的控制法则如下:
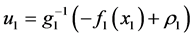 (9)
(9)
其中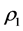 表示虚拟控制量,它的设计基于自适应滑模控制方法。考虑如下滑模面:
表示虚拟控制量,它的设计基于自适应滑模控制方法。考虑如下滑模面:
 (10)
(10)
其中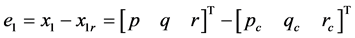 表示角速度误差,
表示角速度误差, 是期望的状态值,
是期望的状态值,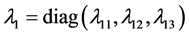 是对角增益矩阵且元素为正常数。
是对角增益矩阵且元素为正常数。
将滑模面对时间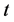 求导得到
求导得到
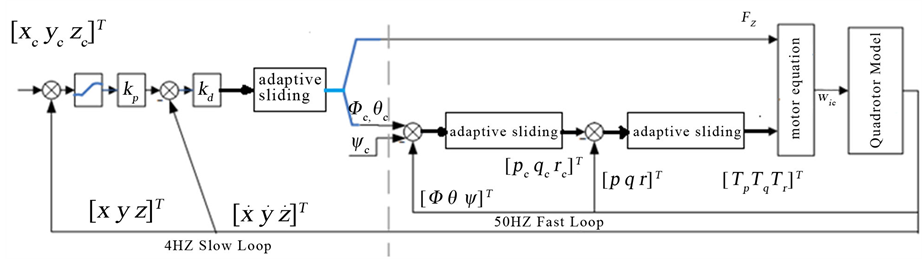
Figure 2. Adaptive sliding mode controller of hierarchical structure for quad rotor
图2. 四旋翼机器人自适应滑模控制结构图
 (11)
(11)
将(9)式代入(11)式有
 (12)
(12)
定义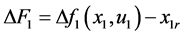
得到
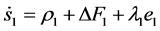 (13)
(13)
式中 为系统的不确定项。
为系统的不确定项。
现作如下假设:系统的不确定项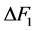 满足
满足
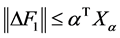 (14)
(14)
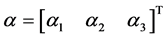

其中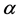 的元素为正常数。
的元素为正常数。
设计如下所示的自适应控制律,可以证明能够实现闭环系统的稳定控制:
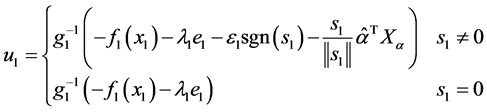 (15)
(15)
式中,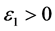 ,
, 为
为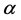 的估计值,且
的估计值,且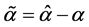 。
。
系统稳定性分析:如果系统满足假设条件(14),采用以上自适应控制律(15),设计如下自适应参数法则,则系统状态将在有限时间内到达滑模面,并使得状态误差收敛于零,保证输出跟踪期望值。
 (16)
(16)
式中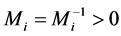 。
。
考虑如下Lyapunov函数:
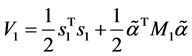
计算其一阶导数,并由(15)、(16)可化简得到:
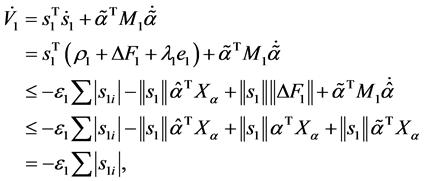 即
即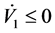
因此,系统状态能在有限时间内到达滑模面 ,实现系统输出渐进跟踪期望值。
,实现系统输出渐进跟踪期望值。
2) 较快回路是飞行器三轴姿态角反馈回路,为最快回路提供角速度指令,设计规则类似于快回路。
根据公式(4)
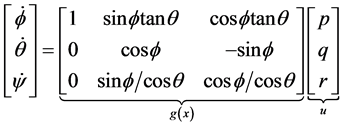
考虑如下仿射非线性方程:
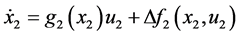 (17)
(17)
定义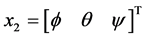 ,
,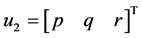 ,
,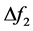 表示系统的不确定项和扰动项,其中
表示系统的不确定项和扰动项,其中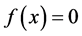 。假设矩阵
。假设矩阵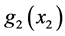 可逆,则较快回路控制法则如下:
可逆,则较快回路控制法则如下:
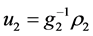 (18)
(18)
定义如下滑模面:
 (19)
(19)
其中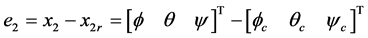 表示姿态角误差,
表示姿态角误差,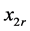 是期望的状态值,
是期望的状态值,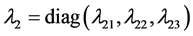 是对角增益矩阵且元素为正常数。
是对角增益矩阵且元素为正常数。
由此得到较快回路的自适应控制律:
 (20)
(20)
式中 ,
, 为
为 的估计值,且
的估计值,且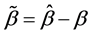 。
。
较快回路自适应参数法则如同最快回路设计,如下:
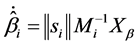 (21)
(21)
根据Lyapunov稳定性分析,同理可证 ,
,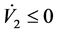 。
。
3.2. 慢回路自适应滑模控制
四旋翼机器人的运动轨迹可以看作是由一系列小的间断点构成,慢回路是其位置的反馈回路,为快回路提供姿态角命令和机体的升力,其响应频率设定为4 Hz。设计规则类似于上面快回路。
假设俯仰角和滚转角很小,由公式(2)和(5)简化可得:
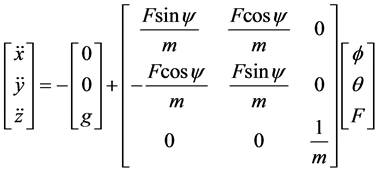 (22)
(22)
对 轴方向运用滑模控制,定义
轴方向运用滑模控制,定义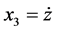 ,
,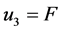 ,
,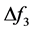 表示系统的不确定项和扰动项,其中
表示系统的不确定项和扰动项,其中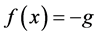 ,
,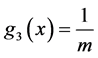 。则慢回路控制法则如下:
。则慢回路控制法则如下:
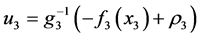 (23)
(23)
定义如下滑模面:
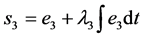 (24)
(24)
其中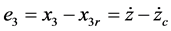 表示沿
表示沿 轴方向线速度误差,
轴方向线速度误差,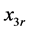 是期望的状态值,
是期望的状态值,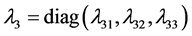 是对角增益矩阵且元素为正常数。
是对角增益矩阵且元素为正常数。
由此得到慢回路的自适应控制律:
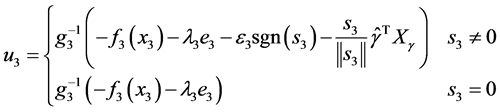 (25)
(25)
式中 ,
,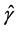 为
为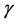 的估计值,且
的估计值,且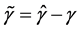 。
。
慢回路自适应参数法则如同快回路设计,如下:
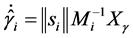 v(26)
v(26)
同理可证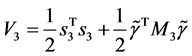 ,
, 。
。
4. 仿真结果
本节将根据上面讲述的控制算法,结合四旋翼机器人的相关参数,对四旋翼飞行轨迹进行仿真。在飞行任务中设置七个航点,从开始起飞经过各航点到最后降落,以此观察该系统的跟踪性能和鲁棒性。表1为四旋翼模型的有关参数值。
由于滑模控制算法被分别用于慢回路和快回路中,因此控制器的有关参数定义如下:
根据控制系统的采样周期,慢回路的自然频率设定为4 Hz,滑模控制器的增益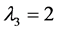 ,切换系数
,切换系数 ,根据公式(22)为较快回路求出
,根据公式(22)为较快回路求出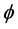 和
和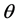 的期望值。而快回路的自然频率为50 Hz,对较快回路而言,控制器的增益
的期望值。而快回路的自然频率为50 Hz,对较快回路而言,控制器的增益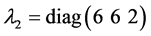 ,
,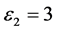 ,根据公式(4)为快回路求出
,根据公式(4)为快回路求出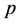 、
、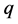 和
和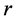 的期望值;对最快回路,控制器增益
的期望值;对最快回路,控制器增益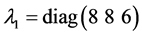 ,
,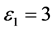 ,再根据公式(7)求出电机转动所需的力矩
,再根据公式(7)求出电机转动所需的力矩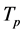 、
、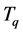 和
和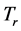 。
。
设置四旋翼飞行器的七个航点,分别为[0 0 10 0;10 0 10 0;10 10 10 0;0 10 10 0;0 5 10 0;0 5 10 3;0 5 0 0]。飞机从原点起飞,依次经过五个航点,并偏航170度,最后降落。图3是飞机在三个轴向上的位置变化情况,图4是飞机在三维坐标系下的轨迹跟踪情况,按照预定的航点进行飞行。可以看出,飞行器飞行稳定,抖振很小。因此,尽管系统存在建模误差和不确定性因素,但由于自适应滑模控制的作用,系统具有很好的跟踪性能和鲁棒性。
图5是飞行器在滚转、俯仰和偏航三个姿态角方向上随时间变化的情况。从航点二经过航点三、航

Table 1. Model parameters in quadrotor
表1. 四旋翼机器人模型参数

Figure 3. The response line of position coordinate
图3. 位置坐标响应曲线
点四经过航点五的过程中,俯仰角发生了小范围的变化。同理,从航点三经过航点四、航点五经过航点六的过程中,滚转角也发生了小范围的变化。在飞行到航点六时,飞行器在此悬停并且偏航170度后逐渐降落至地面。从整个轨迹跟踪过程来看,飞行器在坐标位置发生改变的同时,伴随着自身姿态角的相应变化。
从以上仿真结果可以看出,该算法能够保证四旋翼飞行器飞行稳定,并且跟踪效果良好。
5. 结论
本文针对四旋翼机器人的飞行控制系统,提出了一种自适应滑模控制算法。利用自适应滑模控制使得系统中包含的建模误差,参数变化以及外界干扰等各种不确定性量在有限时间内减小到一个小范围内,
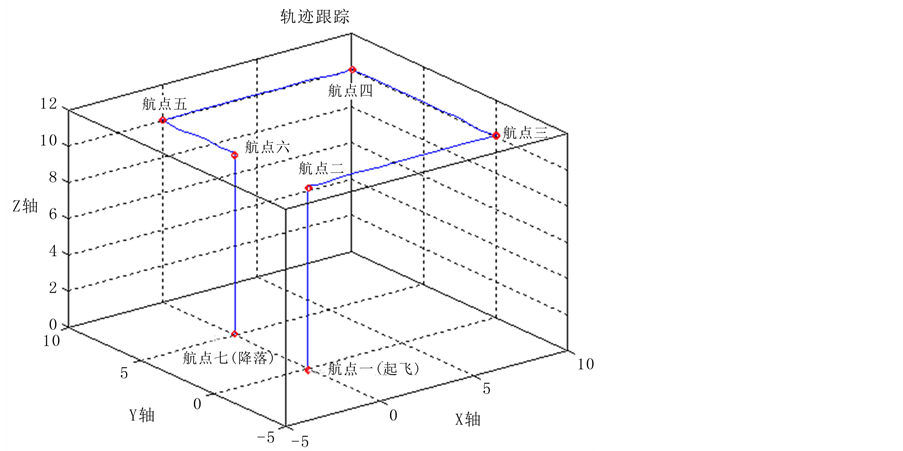
Figure 4. The response line of trajectory tracking
图4. 轨迹跟踪响应曲线

Figure 5. The response line of attitude angle
图5. 姿态角响应曲线
同时消除了系统控制输入的抖振现象,实现系统的渐进稳定和轨迹跟踪。仿真结果表明该方法能够良好得跟踪参考高度和轨迹。