1. 引言
自从Pearson提出三参数微分方程解多种分布函数在β1 (斜度γ1平方)-β2 (峭度)二维平面区域划分后,非正态分布函数的研究取得很大进展[1] [2] 。在失效分析及保险理赔理论中有广泛应用的威布尔分布后来也作为重要成员以一条曲线加入其中[3] 。然而,威布尔分布参数估计诸方法多局限于平均值(一次距)和标准差(二次距)及其组合。而斜度(含三次距)和峭度(含四次距)并未被采用。其原因是多方面的,计算能力不足是其中之一。近几年文献[4] [5] 开始把原始数据的统计量:斜度γ1和过剩峭度γ2对应的形状参数和用极大似然法(MLE)得到的形状参数加以比较,发现它们之间可以相当接近。这样,实测寿命不仅与MLE得到的威布尔分布具有最小方差而且分布形状也正确。本文的主要目的就是研究随机及实测失效数据组的γ1 - γ2曲线如何分布。
2. 计算过程
2.1. 威布尔分布的γ1 - γ2曲线
若已知威布尔分布的形状参数κ,则它唯一确定的斜度γ1和过剩峭度γ2的理论值(期望值)可由下式获得[3] :
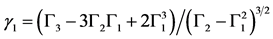 (1)
(1)
 (2)
(2)
式中,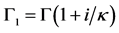 ,其中
,其中 是gamma函数,下标i = 1,2,3,4。
是gamma函数,下标i = 1,2,3,4。
由此得到的威布尔分布的γ1 - γ2以及形状参数κ曲线见图1。其κ曲线的点间隔为0.1,并从左向右逐渐减小。在γ1 = 2 时κ = 1,γ2 = 6,即指数函数分布。而在γ1 = 0时有γ2 = −0.28314,κ = 3.6023。但γ1 = 0.48012时γ2 = 0,κ = 2.252。在图1之后的行文中,把威布尔分布的κ,γ2记为κo,γ2o。
2.2. 模拟和实测寿命数据威布尔分布的γ1 - γ2曲线
2.2.1. 含100随机数的数组
从文献[6] 表中第二列按序取出100个在(0,1)准均匀分布的随机数α。设形状参数κ = 尺寸参数λ = 1,根据下式可计算100个随机数α对应的威布尔准随机寿命L1…L100
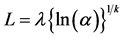 (3)
(3)
然后用极大似然法重新计算截尾数r = 10到100的无序或有序数组的实际形状参数κ。
(1) 100个无序准随机失效寿命的γ1 - γ2曲线
从上述无序准随机失效寿命组采用通用统计软件计算截尾数r分别为10到100的统计量γ1,γ2,然后以γ1为橫坐标,画出γ2,γ2o及κ,κo诸曲线,见图2。其中γ1,γ2,κ分别是数组的斜度,过剩峭度和实际形状参数;γ2o,κo是和γ1对应的威布尔分布过剩峭度和形状参数期望值。为了便于区分,图
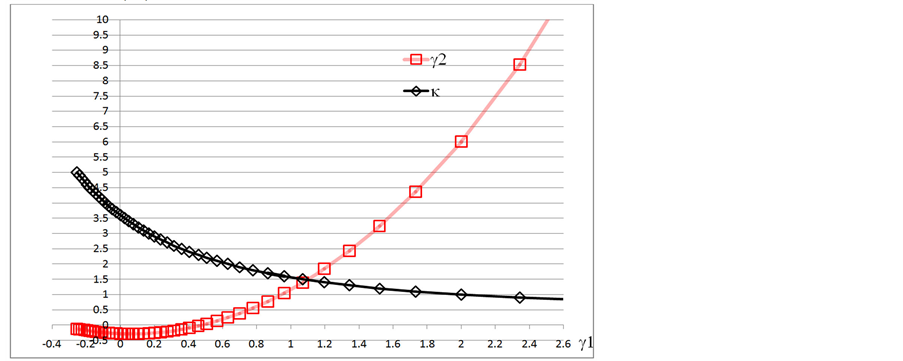
Figure 1. The γ1 - γ2 plot of Weibull distribution
图1. 威布尔分布的γ1 - γ2曲线
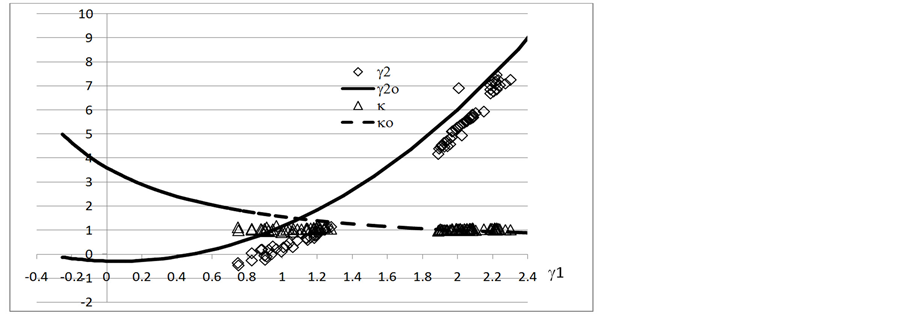
Figure 2. The γ1 - γ2 plot of 100 random life data, right censored from 10 to 100
图2. 100个无序准随机失效寿命的γ1 - γ2曲线,右截尾数从10 至100
中分别用实线和虚线表示威布尔分布的期望值γ2o,κo。而数据组的实测γ2,κ点则只用菱形和三角符号标出。从图中可看出,随着γ1增大,γ2越来越接近但小于期望值γ2o,只有一个γ2高于对应的γ2o。而且在γ1的有值范围,实际形状参数κ只在1附近小幅波动,并在高γ1处和κo相交。显然,在讨论的截尾r范围内数据组均保持良好的随机性。
(2) 100个有序准随机失效寿命的g1 - g2曲线
把上述100个准随机寿命由小到大排列,计算它在截尾数10到100的统计量γ1,γ2。然后以γ1为橫坐标,画出γ2,γ2o及κ,κo诸曲线,见图3。数据从无序变成有序后使得密集分布γ2推向更低的γ1。随后只有三个点分散于高γ1,但未和γ2o相吻合。数据点γ1的最大值也从2.3降到略小于2.0.至于κ,它随γ1增加从2减少到略低于设定值1,几乎和κo相交。
2.2.2. 一组60个7208轴承失效数据的γ1 - γ2曲线
这组由小到大排列的60个寿命数据取自文献[7] 。用2.1节的前60个随机数把它打乱成无序数组,然后分别计算截尾数r由10到60的无序和有序数组的统计量γ1,γ2及κ。并以γ1为橫坐标,分别画出γ2,γ2o及κ,κo诸曲线,见图4和图5。
(1) 60个7208轴承无序准随机失效寿命的γ1 - γ2曲线
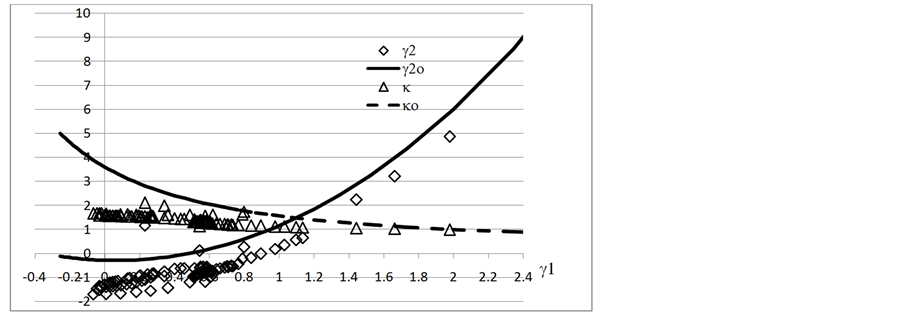
Figure 3. The γ1 - γ2 plot of 100 ascent random life data, right censored from 10 to 100
图3. 100有序准随机失效寿命的γ1 - γ2曲线,右截尾数从10 至100
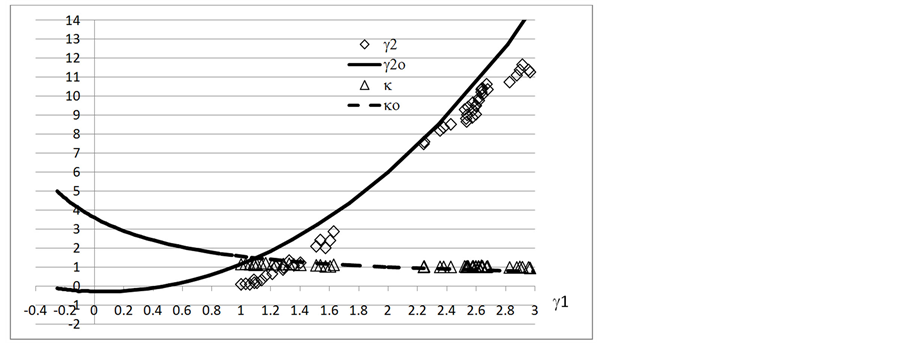
Figure 4. The γ1 - γ2 plot of 60 random life data in 7208 bearing, right censored from 10 to 60
图4. 60个7208轴承准随机失效寿命的γ1 - γ2曲线,右截尾数从10 至 60

Figure 5. The γ1 - γ2 plot of 60 ascent life data in 7208 bearing, right censored from 10 to 60
图5. 60个7208轴承有序准随机失效寿命的γ1 - γ2曲线,右截尾数从10 至 60
图4中试验点也分别集中在低γ1和高γ1两处。数据值γ2相当接近但略小于期望值,而且逐渐逼近γ2o,然后又偏离开。在γ1的有值范围内,实际形状参数κ也在1附近波动并且很快和κo相交。显然,这组数据组在讨论的截尾范围内也保持相当良好的随机性。
(2) 60个7208轴承有序准随机失效寿命的γ1 - γ2曲线
在图5中,数据从无序改成有序后使γ2密集分布区推向更低γ1。随后只有一个γ2点位于高γ1区,它很接近γ2o。数据点γ1的最大值也从3降到略小于2.3。至于κ,它随γ1增大很快从2附近减少到数值1附近,正好和κo相交。
2.2.3. 一组37个H208轴承失效数据的γ1 - γ2曲线
这组由小到大排列的37个轴承寿命数据取自文献[8] 。用2.1节前37个随机数可把它打乱成无序数组,然后分别计算截尾数r由10到37的无序和有序数组的统计量γ1,γ2及κ。以γ1为橫坐标,画出γ2,γ2o及κ,κo诸曲线,见图6和图7。
(1) 37个H208轴承无序准随机失效寿命的γ1 - γ2曲线
图6中试验点分布在三个γ1小区。数据值γ2先是逐渐逼近但略小于期望值γ2o,然后又离开它。在γ1的有值范围,实际形状参数κ也在1附近波动并且很接近κo,但没有相交。显然,这组数据组在讨论的截尾范围内也保持相当好的随机性。
(2) 37个H208轴承有序准随机失效寿命的γ1 - γ2曲线
失效数据从无序改成有序后把γ2密集分布略微推向更低起始γ1。随后只有一个点位于高γ1,而且和γ2o比较接近。数据点γ1的最大值也从2.15附近降到略小于1.8。至于κ,它随γ1增加很快从2减少到1附近,但未和κo相交。请注意,γ2和κ曲线的跳动范围比较大。
3. 结果讨论
从一组100个模拟随机寿命及两组轴承实测寿命(分别为60个和37个数据)的递增截尾γ1 - γ2曲线计算表明:
a) 当疲劳寿命数据组足够大,而且呈准随机分布,在它们的γ1 - γ2图中通常可以在高γ1低κ处找到数据的过剩峭度γ2接近MLE的威布尔分布的γ2o。κo和κ两条曲线的交点和文献[7] [8] 的结果相当接近。这表明,γ1 - γ2图可以作为一种有效的工具和文献[3] [4] 一起用来判断威布尔分布形状参数κ估计的合理性。

Figure 6. The γ1 - γ2 plot of 37 random life data in H208 bearing, right censored from 10 to 37
图6. 37个H208轴承无序准随机失效寿命的γ1 - γ2曲线,右截尾数从10 至 37
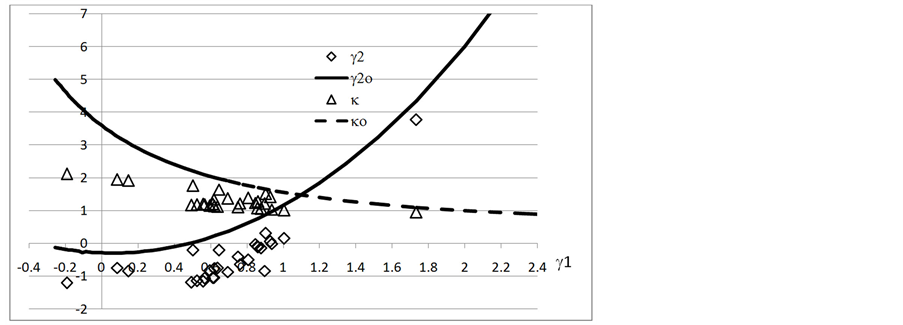
Figure 7. The γ1 - γ2 plot of 37 ascent life data in H208 bearing, right censored from 10 to 37
图7. 37个H208轴承有序准随机失效寿命的γ1 - γ2曲线,右截尾数从10 至 37
b) 一组已知准随机疲劳寿命数据可以分别按有序和无序排列进行MLE截尾计算。如果不同截尾无序数组给出平稳收敛的形状参数κ,则有序数组的κ也有逼近图1中κo曲线的趋势,然而后者的变化区间较大。
c) 随着全样本尺寸从100下降到37,无序与有序数组的形状参数κ逼近期望值κo过程的波动幅度逐步增大。所以,在条件许可时使用较大样本会有更好的统计行为。
d) 当全样本尺寸足够大,经过严格控制试样材料成分,热处理,机械加工,以及寿命试验操作之后如果失效数据还不能得到满意的γ1 - γ2图,也许应考虑其他分布的可能性。
总之,本文以威布尔分布为例说明Pearson及后人的β1 - β2二维图不仅对非正态分布函数的理论研究极其重要,而且对分布函数的实验数据分析有积极的指导意义。