1. 引言
我们越来越多地遇到非饱和土的问题:降雨造成边坡失稳,库水位升降对岸坡稳定性影响,污染物质在土体中的迁移等都会涉及到非饱和渗流问题。从工程角度考虑,我们关心非饱和状态土的力学性质,饱和与非饱和的区别在于饱和土为两相体,而非饱和为三相体,研究非饱和态变化的问题其实就是非饱和渗流的问题。非饱和渗流是个非常复杂的过程,很多学者对其进行了探索,结合前人研究成果,对非饱和渗流取得的成果进行总结,并对其研究进行展望。
2. 非饱和渗流的数值解
在数学方程求解非饱和研究中,1931年Richards [1] 将Darcy的线性渗流理论推广应用到非饱和渗流中以后,人们才开始非饱和渗流研究。在计算机出现以前,对于饱和一非饱和渗流的研究主要是解析法,Philip [2] (1957年)研究了一维垂直入渗的级数解。Parlange [3] (1971, 1972)提出了一种半解析迭代方法,求解地表处为第一类边界(含水率已知)和第二类边界(供水强度已知)的一维垂直入渗问题。上世纪60年代,随着电子计算机的出现,数值方法开始广泛应用,Rubin [4] 研究了二维饱和–非饱和二维Richards方程的数值解,Neuman [5] (1973, 1974)最早将有限元方法应用到解饱和-非饱和渗流问题,他用Galerkin法对Richards方程进行空间域的离散,用Crank-Nicolson有限差分格式对时间域进行离散。Neuman的研究成果后来被人们广泛采用,他的文献因此也成为饱和–非饱和研究方面的经典之作。
上述得到广泛研究的饱和–非饱和渗流都是基于Richards控制方程的,它忽略了空气相的流动,仅仅考虑水相在土中的流动。然而严格意义上的非饱和渗流理论应当考虑空气和水的两相流。但是在土坡稳定分析工作中,一般忽略空气流动和体变的影响,采用简化的Richards方程进行计算。这种简化模型在分析中是否会引起以及何种情况下会引起重要的偏差,至今还未进行系统深入的研究。Fredlund和Hasan [6] (1979)提出了求解非饱和土固结过程中孔隙气压力和孔隙水压力的两个偏微分方程。该方程假定气相是连续的,Darey定律和fick定律分别适用于气相和水相的流动,并认为水相和气相的渗透系数都是土的基质吸力或某一体积–质量的函数,通常称之为两相流方法。邵龙潭[7] (2000)对气体排出和水分入渗运动进行了试验研究,并用数值模拟方法进行对比。他认为在研究水流入渗问题时,对一些导气率较低的土类,考虑气相的压缩和运动的影响是必要的。
3. 饱和度对渗透系数的影响
而在岩土工程应用中,非饱和渗流比纯数学问题考虑的问题要复杂。在非饱和土中,渗透系数受到空隙比和饱和度的影响,土中的水只能通过水所填充的空隙空间流动,所以冲水空隙所占比例是影响渗透性的一个重要因素。土越干,土中含水量越小,则透气性越大,透水能力越弱。当一种土变成非饱和时,大空隙水的吸力较低,而小空隙的吸力较高,首先排除大空隙的水,导致水通过较小的空隙流动,增加了流程的弯曲度,使渗透系数降低。另外土的含水量越小,土中水和颗粒表面距离越近,相互作用更加强烈,从而使水的流动阻力也增加。非饱和渗透系数是一个随饱和度变化的量,研究结果表明,渗透系数与饱和度的函数关系不受滞后作用的影响。
近年来,研究一般根据土水特征曲线间接计算非饱和渗透系数,采取的数学模型如表1。
表中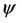 为吸力,
为吸力,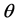 为体积含水量,和
为体积含水量,和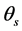 和
和 已分别为饱和以及残余体积含水量,
已分别为饱和以及残余体积含水量, 为有效饱和度,其他符号为各模型的各自的拟合参数。在这些模型中,Brooks & Corey (1964)模型最为简单,模型中的参数也具有明确的物理意义,而 Van Genuchten M.T. [7] 模型和Fredlund D.G. & Xing A.模型的拟合效果最好,这三个模型是目前非饱和土力学中最常用的模型。
为有效饱和度,其他符号为各模型的各自的拟合参数。在这些模型中,Brooks & Corey (1964)模型最为简单,模型中的参数也具有明确的物理意义,而 Van Genuchten M.T. [7] 模型和Fredlund D.G. & Xing A.模型的拟合效果最好,这三个模型是目前非饱和土力学中最常用的模型。
Vanapalli和Labbezoo (2002)通过实验发现土壤的渗透系数与饱和度在双对数坐标系可以近似成为一条直线,如果对饱和度S进行修正,得到修正饱和度 (
( 为与塑性指数有关),存在良好的线性关系,提出了渗透性模型,建立了相对渗透系数与修正饱和度
为与塑性指数有关),存在良好的线性关系,提出了渗透性模型,建立了相对渗透系数与修正饱和度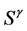 的关系表达式:
的关系表达式:
 (1)
(1)
梁爱民 [8] (2008)年曾用实验得到渗透系数与上述两种渗透系数求得的渗透系数进行对比分析,表明两种模型的拟合实验结果与实验结果存在一致性。
在使用上述土水特征曲线模型时,应首先测定土水特征曲线试验散点,然后运用模型拟合这些散点得到连续函数,最得出其相关方程。从过程可以看出,在使用这些模型时,根据试验散点拟合标定的参数值是否准确,得到的函数能否正确地反映土的孔隙结构特点和它的持水能力,是模型能否成功应用的关键所在,所以应首先选择合理模型,并在试验中选取关键离散点进行拟合,结果会更准确。
4. 变形对非饱和渗透系数的影响
非饱和渗流模型一般来源于土壤学,土壤研究对象一般为表层土壤,受力简单,一般不考虑变形对渗透性的影响,在非饱和土力学中,研究对象一般在复杂应力条件下,研究问题一般与变形有关,许多学者对变形对非饱和渗流的研究,Mitchell [9] (1965)提出了反映空隙比和含水量影响的非饱和土渗透模型:
 (2)
(2)
表1. 土水特征曲线拟合方程
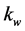 为非饱和渗透系数;
为非饱和渗透系数;
 、
、 、
、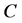 为空隙比,饱和度和模型参数。
为空隙比,饱和度和模型参数。
Lloret和Alonson [10] (1980)也提出相似的模型,变形对非饱和土渗体现在空隙比的变化上,这类模型对砂性土预测效果较好,而对粘性土效果不理想。该类模型中变形对渗透性影响只表现为空隙大小的影响,而空隙分布规律的变化无法体现。
为了更加准确预测变形对渗透性的影响,张雪东(2010) [11] 从流体力学出发,以概率论数学推导出能够考虑空隙结构影响的渗流系数表达式,结合Mualem [12] (1976)提出了相对渗透系数计算模型,空隙结构参数与变形的变化规律,得到了能够考虑不同密度状态下非饱和渗透系数的计算模型。但是该模型很复杂,参数较多,并未得到广泛应用。
5. 封闭气泡对非饱和渗透性的影响
在非饱和土体入渗过程中,气体容易被封闭在空隙裂隙中,形成不连续的气泡。封闭气泡的存在对水相流动形成阻碍作用,使土体的渗透性能降低。
Constantz [13] (1988)等人的研究表明,一部分的封闭气泡会停留在土壤空隙中,封闭气泡的影响使非饱和渗透系数最大比初始值降低80%。Jaoudat (1986)通过实验与计算机模拟得出当气体可以从入渗湿润锋前自由溢出时,气体溢出的粘阻力对入渗影响可以忽略不计,而当气体仅能从入渗表面溢出时,湿润锋前的压缩气体是单值入渗系数降低的主要原因。国内学者孙冬梅[14] (2008)建立了水–气二相流模型,验证了空隙气压力的增大对入渗产生的阻碍作用,指出降雨入渗时,如果忽略封闭气泡对渗透的影响,会产生很大的误差。张华[15] (2009)在前人研究成果的基础上,通过室内一维入渗实验初步探讨了封闭气泡形成的原因及对入渗性能的影响。
气泡含量的影响因素主要包括以下几个方面:①干密度的影响,干密度越小,土体气体难以排出,对入渗阻力越大;②土壤性质的影响,低液限土剖面含水量呈台阶状,而粉土质砂的入渗含水率分布台阶状不明显;③原始含水量的影响,含水量越小,入渗时土体的气体排出越困难,封闭气泡含含量较大。封闭气泡对入渗作用主要体现在两个方面,一方面封闭气泡的存在使入渗系数减小,另一方面气泡在湿润锋前压缩,气压逐渐增大,对水流的入渗起阻碍作用。
6. 结论
在非饱和渗流研究方面,很多学者对其机理及影响因素进行了探索,但是非饱和渗流是一个非常复杂的问题,考虑的因素较多,而耦合计算非常的困难,目前耦合全部因素是困难的,采用的方法一般从饱和度的角度进行计算的。
在岩土工程应用中,非饱和渗流研究取得了很多研究成果,但主要以数值方法为主,出现了很多重复的研究,应该加强原位实验研究,从实际情况建立渗流模型会更符合实际情况。