1. 引言
金属多层薄膜的制作方法有很多种,最常用的是通过物相沉积的方法控制薄膜的厚度在纳米级数范围内。近年来研究物相沉积的薄膜系统有很多,金属–金属、金属–非金属、金属–陶瓷相等。这些材料是通过改变金属多层薄膜相组成的基础下,在微米级至纳米级的尺寸级数来研究薄膜的强化机制[1] 。金属多层膜由于表面以及界面的存在,在加载过程中表现出一个明显的尺寸效应[2] ,而且,在不同的加载条件下,变化不同。然而,纳米金属多层膜的力学性能的研究主要是通过单轴拉伸试验和纳米压痕的测验来获得,如Misra等[3] 利用溅镀沉积制作Cu-Nb多层分子膜通过纳米压痕试验,来测定薄膜尺寸厚度与屈服应力的关系。早期也有相关的一些研究,而且大多数是以FCC/FCC薄膜结构为研究对象[4] 。
本文是通过建立多层的BCC/FCC结构的Fe/Ni薄膜模型,控制薄膜单层组元的厚度,对垂直于Fe、Ni原子结合面进行单向拉伸,重点研究薄膜单层厚度与薄膜屈服应力之间的关系。此外,还对Fe/Ni合金薄膜的变形机制进行了探究,通过研究Fe-Ni薄膜力学性能的尺寸效应及缺陷演化规律,探寻多层薄膜材料的强化机制,可望通过控制材料的微观结构和内部界面微结构为制备具有性能更好的材料奠定基础。
2. 模拟方法
建立Fe/Ni多层薄膜组元厚度相等的模型,组元单层厚度在6~26 nm之间变化,本文Fe、Ni原子晶格常数分别取0.2863 nm、0.3524 nm,由于二者晶格常数相差较大,Fe、Ni晶格常数之比约为0.8124,因此可通过控制Ni、Fe原子的层数比为0.8124来控制薄膜组元厚度相等。
如图1所示,为Fe、Ni组元厚度相等的原始模型,白色为Ni原子,绿色为Fe原子,采用三向周期边界条件,对薄膜系统沿垂直于组元接触面的方向进行单向拉伸,模拟中原子间相互作用势采用EAM势函数[5] ,模拟是采用Sandia国家实验室提供的MD代码LAMMPS进行的,时间步长设定为1 fs,为消除原子间的内应力,对体系用npt系综在1K温度下充分弛豫,在相同温度下进行等应变拉伸,拉伸速率为10−9 s−1,拉伸至断裂为止。同时,为了区分完整晶体、位错、堆垛层错以及表面原子,我们采用中心对称参数法来分析薄膜的微观结构演变。
3. 结果及讨论
3.1. 应力应变关系
应力应变关系反应的是材料的应力随着应变的变化的关系,在材料的力学研究中起着非常重要的作用,一般来说,不同的材料其应力应变的关系是不一样的。图2表示的是Fe/Ni多层薄膜不同组元厚度

Figure 1. Curve: The initial model of multilayer thin film system. Green for Fe atoms, white for Ni atoms
图1. Fe/Ni多层薄膜系统的初始模型。绿色为Fe原子,白色为Ni原子

Figure 2. Curve: The different individual layer thickness of thin film tensile stress strain curve
图2. 薄膜不同组元厚度拉伸时应力应变曲线图
拉伸的应力应变曲线图。
从图2中可以看出,随着薄膜单层厚度的减小,薄膜的屈服应力也随之增加,断裂伸长率也随之增加,即薄膜的延展性随着薄膜的单层厚度的减小而增加,符合传统的强化机制。为此,为进一步探究薄膜单层厚度减小对薄膜的影响,继续减小薄膜单层组元的厚度,拉伸应力应变曲线如图3所示,可以看出在薄膜单层厚度约为10.6 nm~15.18 nm时,屈服应力不再增加,在一定的范围内波动;当薄膜单层厚度继续减小时,薄膜的屈服应力不再增加,反而呈逐渐减小的趋势。Misra等[3] 指出,多层膜的峰值强度/硬度是由单根位错穿过界面所需的应力决定的,屈服应力呈现这种趋势,说明随着薄膜单层厚度的增加,界面对单根位错的阻力产生了变化。从图上可以看出,Fe/Ni多层薄膜的断裂伸长率与屈服应力的变化趋势一致,屈服应力在最大值区域波动时,薄膜的断裂伸长率也呈现出相应的趋势,由此可以看出,当Fe/Ni多层薄膜单层厚度在10.6 nm~15.18 nm时,薄膜表现出了最佳的力学性能,具有较好抗拉强度和延展性。而从传统的薄膜强化机制来看,随着薄膜单层厚度的减小,薄膜的屈服应力会呈现增大的趋
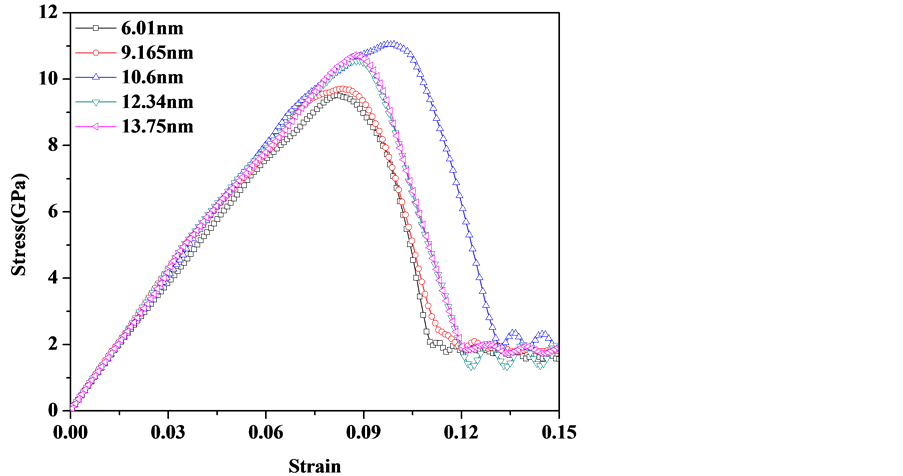
Figure 3. Curve: The different individual layer thickness of thin film tensile stress strain curve
图3. 薄膜不同组元厚度拉伸时应力应变曲线图
势,但是图中在薄膜单层厚度约在10.6 nm~15.18 nm时屈服应力不再增加,而是在一定的范围内波动,在薄膜单层厚度小于10.6 nm后甚至表现出减小的趋势,显然,这与传统的强化机制相反。上述迹象表明了多层薄膜的屈服强度、断裂伸长率对薄膜的单层厚度有着明显的尺寸依赖性,而出现这种现象的主要原因是否是由于薄膜的变形机制发生了变化,因此,我们下面对其变形机制进行了分析。
3.2. 尺寸效应及变形机制
目前,大多数研究结果显示,金属多层薄膜的强度不是随着薄膜单层厚度的减少而增大的[3] [6] 。图4表示的是Fe/Ni多层薄膜屈服应力随薄膜单层厚度变化的曲线图,我们可以看出,Fe/Ni多层薄膜的屈服强度对薄膜尺寸有着明显的依赖性,这与以前大多数金属薄膜的变化趋势是相符合的[7] ,而为了探索变形机制的变化,我们给出了Fe/Ni多层薄膜在拉伸变形过程中的结构演化图,如图5所示,蓝色表示完整晶体结构的原子,绿色表示位错、滑移的原子团,红色表示表面原子、界面原子。
当薄膜的单层厚度大于15.18 nm时,多层膜的强硬度与薄膜单层厚度遵从经典的Hall-petch等式关系[8] :
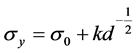 (1)
(1)
其中σy为薄膜的屈服应力,σ0为移动单个位错时产生的晶格摩擦阻力,k为常数,d为晶粒平均尺寸(或薄膜层厚)。即多层膜的强硬度随着薄膜特征尺寸的减小而增大,因为Fe、Ni组元交接界面的位错交互作用导致位错滑移受到约束[9] ,被界面定扎的单根位错被限制在软相层内滑移[10] ,使得单根位错、滑移等只能在组元内进行,如图4中单层厚度为18.33 nm厚度时的结构演化中绿色原子所示,位错被限制在组元内滑移堆积,这种位错机制符合典型的Hall-petch关系的位错塞积机制,而且多层薄膜的屈服应力随着薄膜厚度的增加而减小,符合经典的Hall-petch关系。
随着薄膜单层厚度的减小,当薄膜当层厚度减小到仅能容纳一个单根位错时,如图4中薄膜单层厚度为10.6 nm的拉伸结构演变图中绿色原子所示,此时,位错被界面定扎,在组元内会呈现出一个弓形,因此它的变形机制也从开始的位错塞积机制转变成为位错弓出机制,而且,此时的Fe/Ni多层薄膜有较

Figure 4. Fe/Ni multilayer film yield stress along with the change of individual layer thickness graph
图4. Fe/Ni多层薄膜的屈服应力随特征尺寸的变化曲线图

Figure 5. Fe/Ni multilayer film yield stress along with the change of individual layer thickness graph
图5. Fe/Ni多层薄膜的屈服应力随特征尺寸的变化曲线图
好的屈服强度,如图3所示,由于随着薄膜单层厚度的减小,薄膜组元内容纳的单根位错有时会大于一个,因此,在薄膜单层厚度为10.6 nm~15.18 nm范围内,Fe/Ni多层薄膜的屈服强度在一定的范围内波动。当薄膜单层厚度进一步减小时,薄膜的单层厚度已容纳不下一个单根位错,此时,被界面钉扎的单根位错会贯穿整个单层组元,如图4中薄膜单层厚度为6.01 nm时的拉伸结构演变图中绿色的原子所示,此时多层薄膜的变形机制转变为贯穿界面机制。因为当单根位错贯穿整个组元层时,克服了Fe、Ni组元界面的阻力,使得Fe/Ni多层薄膜的屈服强度急剧下降,当薄膜单层厚度为10.6 nm减小至9.165 nm时,它的屈服强度从11.04 GPa下降至9.7 GPa,此时,多层薄膜的屈服应力随着薄膜单层厚度的减小而减小,表现出了一个明显的反Hall-petch关系。
基于以上分析,Fe/Ni多层薄膜的屈服强度对组元单层厚度有着明显的依赖性,而在拉伸过程中塑形变形机制的改变是引起屈服强度明显变化的主要原因,而在变形过程中被界面钉扎的单根位错在变形机制中起着重要的作用。然而,在纳米晶金属材料中,它主要是从晶界和晶粒间界局部位错发射来协调塑性变形[11] 。因此,Fe/Ni多层薄膜的变形机制不同于纳米晶金属材料,Fe/Ni多层薄膜的变形机制主要是依靠单根位错来实现的。
4. 结论
Fe/Ni多层薄膜的屈服应力、断裂伸长率对薄膜的单层厚度有着明显的尺寸依赖性,模拟结果显示,在薄膜单层厚度大于15.18 nm时,屈服应力与薄膜单层厚度符合经典的Hall-petch关系,即随着薄膜单层厚度的增大,屈服应力减小,此时,Fe/Ni多层薄膜的变形机制表现为位错塞积机制;当薄膜单层厚度减小,在单层厚度约为10.6 nm~15.18 nm之间时,屈服应力呈现出最大值,断裂伸长率也是一样,即Fe/Ni多层薄膜表现出良好的抗拉性能以及延展性,此时,Fe/Ni多层薄膜呈现出的是位错弓出机制;当薄膜单层厚度进一步减小时,在薄膜单层厚度小于10.6 nm,屈服应力与薄膜单层厚度呈现出反Hall-petch关系,即随着薄膜单层厚度的减小,屈服应力减小,此时的变形机制为贯穿界面机制。而在整个变形机制变化中,主要是依靠单根位错来实现的。
致谢
本次工作是在陈老师的指导下,以金属材料晶粒的尺寸效应为基础,进一步开展的一个研究工作,在此感谢陈老师的指导帮助,同时也感谢国家科学基金给予的支持以及参考文献中为我提供指导作用的各位研究工作者。