1. 引言
自1998年我国开启住房制度改革以来,房地产行业得到了快速的发展。随着国民财富的积累以及城镇化的影响,民众对房地产住宅的需求逐渐增加,导致我国房地产市场长期处于供不应求的状态,因而近些年中国房价一路走高。
另一方面,由数据显示(雷中英,2011) [1] ,如果将房屋建设和使用过程中的能耗折算为碳排放,新建1平方米的房屋就要排放约0.8吨二氧化碳,结合2013年的房屋竣工面积来看,仅这一年的新建竣工房屋就带来了8.1亿吨二氧化碳排放。因此,房地产行业的碳排放所引起的环境污染问题不容小觑。针对这一问题,近年来国家发改委和财政部也不断提出关于碳税开征的构想,碳税这一问题越来越引起关注。
基于以上研究背景可知,房价问题与碳排放带来的环境问题在我国均比较严峻。一方面,环境问题要求我们开征碳税,以此来促进节能减排;另一方面,根据经济学理论易知,碳税的开征将导致房地产行业建造成本的增加,其他因素不变的情况下,会导致房价升高。所以,从调控房价这一角度来看,碳税的开征将面临很大的质疑与挑战。
时至今日碳税仍未开征,因此国内学术界对其与房价相关性的研究还很少,而关于房产税的研究却相对较多。本文将碳税与房价这两个热点问题结合起来,做一些前瞻性的研究,在研究方法上借鉴了前人对于房产税与房价相关性这一问题的研究。
国内对于房产税的研究较多,研究方法主要分为理论研究与实证分析两大类。如陈多长(2004) [2] 通过逻辑演绎以及简单的理论建模研究了房产税对住宅资产价格的影响,认为房产税在长期内会降低住宅资产的均衡价格,而在短期内会导致房租的提高。而睢党臣(2011) [3] 则持不同观点,通过对重庆、上海两个房产税改革试点城市的研究,运用逻辑演绎与作图的方法,得到结论:短期来看,房产税的出台能或多或少抑制高房价,而从长期看,则不能将抑制房价的希望寄托于房产税上。况伟大(2012) [4] 则在理论建模基础上,根据23个OECD国家30年的住房市场数据进行了实证研究,最后得到结论:房产税政策能有效抑制房价,但具有一定局限性;预期对房价的影响要高于房产税,因此改变房价增长预期的政
策比房产税政策更为有效。
本文主要分为三部分,先进行理论建模来研究碳税对房价的影响,然后通过实证分析来估算这一影响程度的大小,最后根据以上两部分的研究结果得出结论并给出政策建议。
2. 理论模型
2.1. 消费者模型
2.1.1. 模型假设
假设1:消费者同质,追求终生效用最大化。
假设2:消费者一生分为两期。青年时期工作赚取收入,可支配收入为Y,用于当期消费一般性商品、购买住房和支付房屋使用成本;老年时期卖出房屋(其住房需求可认为由子女解决或由政府部门解决),所得收入仅用于当期消费1。
假设3:一般性商品价格标准化为1,作为价格测度2。
假设4:效用函数的形式为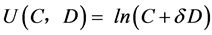 3其中
3其中 分别表示一般性商品消费量和购房数量,
分别表示一般性商品消费量和购房数量,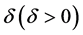 表示房屋带来的效用和一般性商品带来的效用之间的转换因子;第二期时,消费者卖出其拥有的所有房屋,此时效用函数退化为
表示房屋带来的效用和一般性商品带来的效用之间的转换因子;第二期时,消费者卖出其拥有的所有房屋,此时效用函数退化为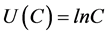 。
。
假设5:消费者对住宅的需求函数为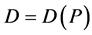 。
。
2.1.2. 假设解释
假设1意味着任何一个消费者均具有代表性,在不失一般性的前提下简化了建模过程。消费者终身效用最大化的假设与经济学理论相符。
假设2借鉴了戴蒙德(Diamond)代际交替模型中的基本假设,考虑了消费者的延续消费行为,与现实更为相符。
假设3中把一般性商品价格标准化为1,以此来研究另一种商品的消费情况,这也是经济学建模的常用方法。
效用函数的一般性假设是 ,
,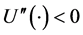 。显然,假设4中的效用函数满足这两个要求。
。显然,假设4中的效用函数满足这两个要求。
假设5没有给出需求函数的具体形式,更具有一般性。
2.1.3. 消费者效用最大化
1简便起见,这里将除住房以外的其他所有商品归为一般性商品。
代表性消费者的效用最大化问题表述为:
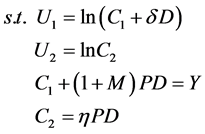
其中: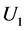 和
和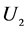 分别表示第一期和第二期的效用;
分别表示第一期和第二期的效用;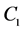 和
和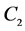 分别表示第一期和第二期的一般性商品消费量;
分别表示第一期和第二期的一般性商品消费量; 表示两期之间的效用贴现因子;
表示两期之间的效用贴现因子; 表示房屋折旧因子,即在第一期价值为
表示房屋折旧因子,即在第一期价值为 的房屋的第二期价值为
的房屋的第二期价值为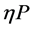 ;
;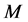 表示单位房价住房使用成本,根据Himmelberg (2005) [5] 的研究,
表示单位房价住房使用成本,根据Himmelberg (2005) [5] 的研究,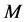 可表示为
可表示为 ,
, 表示无风险利率即购房的机会成本,
表示无风险利率即购房的机会成本,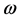 表示房产税,
表示房产税,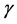 表示维修费用,
表示维修费用,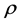 表示购房相对租房的风险溢价,
表示购房相对租房的风险溢价, 表示本期的房屋资本利得。
表示本期的房屋资本利得。
等价地,上述问题可表述为:
求解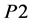 可得到以下命题:
可得到以下命题:
命题1:当满足一定条件时4,有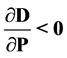 。
。
证明:由一阶条件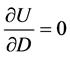 可得:
可得: 。所以当
。所以当
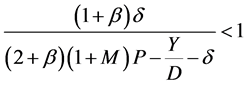 ,即
,即 时,有
时,有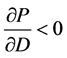 ,
, 。 Q.E.D.
。 Q.E.D.
命题1表明,当满足一定条件时,需求函数是向下倾斜的,这与经济学理论相符。
2.2. 房地产商模型
2.2.1. 模型假设
假设1:房地产行业中有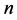 个同质的房地产商,均追求利润最大化。
个同质的房地产商,均追求利润最大化。
假设2:碳税为从量税5,仅对厂商征收,税率为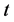 。单位面积房屋建造过程中产生的CO2碳排放为
。单位面积房屋建造过程中产生的CO2碳排放为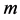 。
。
假设3:单位面积房屋建造成本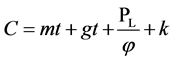 ,其中
,其中 来源于建材价格上涨导致的建造成本的
来源于建材价格上涨导致的建造成本的
增加(碳税征收将导致二氧化碳高排放的建材行业生产成本增加,从而建材价格上涨,进一步导致房屋建造成本上升),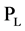 为单位面积土地价格,
为单位面积土地价格, 为容积率(建筑面积除以占地面积),
为容积率(建筑面积除以占地面积), 表示其他成本。
表示其他成本。
假设4:住宅市场出清6。
假设5:房地产商面临的需求函数为同消费者模型中需求函数。
2.2.2. 假设解释
假设1意味着任何一个房地产商均具有代表性,在不失一般性的前提下简化了建模过程。房地产商追求利润最大化的假设与经济学理论相符。
假设2意味着房地产商在最大化自己的利润时,必须将碳税政策考虑在内,在这点上与消费者不同。
假设3中考虑了碳税对房屋建造成本的直接影响和间接影响,这与实际情况基本相符。

4这里指要满足消费者模型的假设且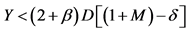 。
。
5考虑到课税对象的性质,使用从量税较为合理。
6这一假设可能与现实不符,但其对结论并不会造成显著影响,作出这一假设仅是为了简化模型推导过程。
假设4意味着房地产商的住房供给等于消费者的住房需求。
假设5意味着房地产商在最大化自己的利润时,还必须将消费者的效用最大化行为考虑在内。
2.2.3. 房地产商利润最大化
第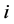 个代表性房地产商利润最大化问题表述为:
个代表性房地产商利润最大化问题表述为:
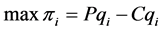
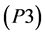
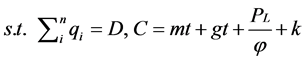
求解P3可以得到以下命题:
命题2:当满足一定条件7时,碳税的征收将导致均衡房价的上涨以及均衡房屋交易量的下降。
证明:由一阶条件 可得:
可得: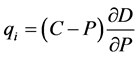 (1)。根据假设1和4可知,
(1)。根据假设1和4可知,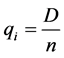 。所以,(1)式可化简为
。所以,(1)式可化简为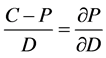 。根据消费者模型的结论
。根据消费者模型的结论 ,可求得
,可求得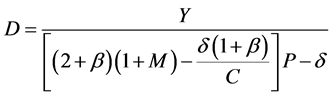 。比较静态分析可知
。比较静态分析可知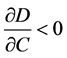 ,
,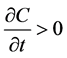 。根据链式求导法则,
。根据链式求导法则,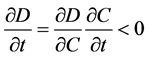 ,
, 。 Q.E.D.
。 Q.E.D.
命题2的结论可结合简单的示意图进行阐述:
7这里指要满足命题1中的条件以及要满足房地产商模型的假设。
8本文在实际理论建模时,考虑到参数较多以及求解的复杂性,并未给出需求函数以及均衡房价的具体表达式,仅大概参照了图2所示的建模思路。
根据图1,碳税开征前的房屋供给、需求曲线为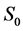 、
、 ,均衡房价和房屋交易量为
,均衡房价和房屋交易量为 、
、 。碳税开征后,由于建造成本的上涨,其他因素不变的情况下,相同价格水平下房屋供给减少,所以供给曲线左移。此时,均衡房价为
。碳税开征后,由于建造成本的上涨,其他因素不变的情况下,相同价格水平下房屋供给减少,所以供给曲线左移。此时,均衡房价为 ,均衡交易量为
,均衡交易量为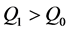 。可以看到,图示法得到的结果与上述模型的结果相同:碳税的征收会导致均衡房屋交易量下降,均衡房价上涨。
。可以看到,图示法得到的结果与上述模型的结果相同:碳税的征收会导致均衡房屋交易量下降,均衡房价上涨。
理论模型的建模思路可表示为图2:1) 消费者将房价视为外生给定来最大化自己的效用从而确定需求量;2) 房地产商将碳税税率视为外生给定并根据消费者的最优反应函数(即需求函数)来最大化自己的利润从而确定房价8;3) 利用1)、2)的结果可以确定均衡房屋交易量和均衡房价;4) 政府根据均衡房价
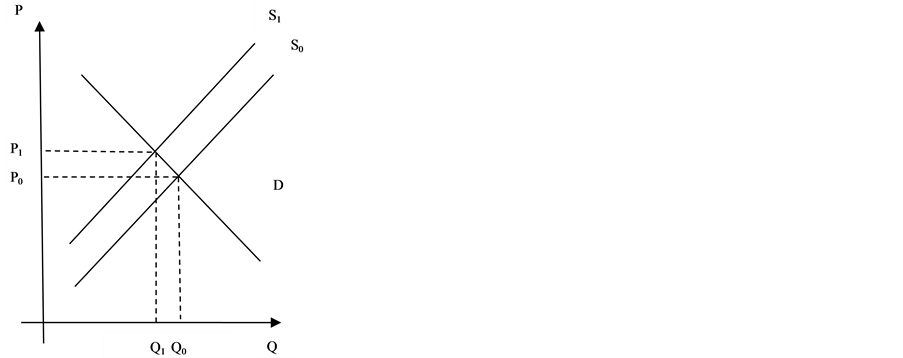
Figure 1. Pre-tax & post-tax housing prices and housing transaction volume
图1. 碳税征收前后均衡房价和均衡房屋交易量变化图
以及均衡房屋交易量来制定碳税税率。
但在现实中,政府先制定碳税税率,消费者通过效用最大化确定需求量,房地产商根据需求函数和碳税税率来最大化自己的利润从而确定房价和供给量。只不过政府在制定碳税税率时会预见到消费者和房地产商的行为,并据此确定一个合理的税率水平。
3. 实证分析
为了进一步研究碳税对房价的影响,我们在此部分建立房价模型来实证测算这一影响程度的大小。通常的研究思路是:将房价作为被解释变量建立房价模型来研究碳税这一解释变量对房价的边际影响。但由于我国仍未开征碳税,所以这一研究方法受到了极大限制,必须另辟蹊径。本文的研究思路如下:首先,碳税是通过影响房屋建造成本来影响房价的,可以通过研究建造成本对房价的边际影响以及碳税对建造成本的影响进而得知碳税对房价的边际影响。碳税对房屋建造成本有直接和间接两方面影响:由于房屋建造过程会带来大量二氧化碳排放,碳税的征收直接导致建造成本的上升;建材行业也是二氧化碳高排放行业,碳税的开征将导致建材生产成本增加,进而抬高房屋建造成本。而建造成本对房价的边际影响可以通过建立房价模型得到。
3.1. 房价模型
针对高房价这一问题,国内外学者做了大量研究,建立了很多房地产定价模型。现有的定价模型大致可划分为三类。第一类:从住宅特征因素(如地理位置、房屋面积、房间数量)这一角度对房价进行解释。比如,SELİM (2008) [6] 用土耳其2004年的家庭预算调查数据、温海珍(2004) [7] 用杭州市的住宅交易资料均说明了房屋面积、房间数量等住宅特征因素可以很好地解释当地房价。第二类是从房地产开发用地这一角度研究高房价。比如,况伟大(2005) [8] 从地价的角度研究房价,主要结论是短期内房价和地价相互影响,长期内地价是房价的Granger原因。而施建刚(2013) [9] 从土地供给的角度研究房价,主要结论是增加土地供给量能显著抑制房价上涨,但住房供地对房价的影响具有一定滞后性。第三类是从宏观经济变量(如人均GDP、利率、CPI)这一角度进行建模。比如,王浦(2008) [10] 用回归分析方法确定了房价的决定因素为住宅建设成本、居民可支配收入、就业率、利率、住宅建筑面积、住宅销售额、城镇人口增长率。Craig (2011) [11] 结合香港房地产数据用实际人均GDP、建造成本、土地供给、实际利率等宏观经济变量很好的解释了当地房价。而Madsen (2012) [12] 则进一步从长短期分别进行研究,主要结论是房价在短期内由整个经济的名义收入和名义住房贷款利率决定,在长期由购置成本所决定。根据研究需要,本文建立的房价模型属于第三类。
根据微观经济学理论可知:


即房屋供给量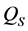 是房价
是房价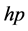 、建造成本
、建造成本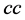 、土地成本
、土地成本 以及企业贷款利率
以及企业贷款利率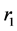 的函数,房屋需求量
的函数,房屋需求量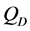 是房价
是房价 、人均可支配收入
、人均可支配收入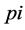 、人口密度
、人口密度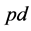 以及住房贷款利率
以及住房贷款利率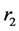 的函数。从供给曲线来看:价格的变化仅仅会导致供给量沿着曲线移动,而建造成本、土地成本以及利率这些影响房地产开发成本的因素的变化带来的是供给曲线的整体移动;从需求曲线来看:价格的变化会导致需求量沿着曲线移动,而人均可支配收入、人口密度以及住房贷款利率这些因素的变化带来的是需求曲线的整体移动。
的函数。从供给曲线来看:价格的变化仅仅会导致供给量沿着曲线移动,而建造成本、土地成本以及利率这些影响房地产开发成本的因素的变化带来的是供给曲线的整体移动;从需求曲线来看:价格的变化会导致需求量沿着曲线移动,而人均可支配收入、人口密度以及住房贷款利率这些因素的变化带来的是需求曲线的整体移动。
上述供给、需求函数具体地可以写为:
 (1)
(1)
 (2)
(2)
其中,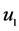 表示除了(1)式中的解释变量之外的影响房屋供给的因素,
表示除了(1)式中的解释变量之外的影响房屋供给的因素,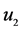 表示除了(2)式中的解释变量之外的影响房屋需求的因素。
表示除了(2)式中的解释变量之外的影响房屋需求的因素。
(1)和(2)式为结构模型,而在现实中,我们观测到的一般是均衡值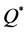 ,即
,即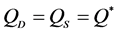 ,所以房价与解释变量之间的关系可以表述为以下简约模型(3):
,所以房价与解释变量之间的关系可以表述为以下简约模型(3):
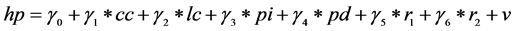 (3)
(3)
其中: 、
、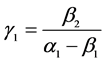 、
、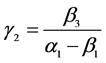 、
、 、
、 、
、 、
、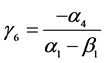 、
、 。
。
3.1.1. 数据来源及数据处理
根据房价模型,我们收集了2002~2013年全国31个省直辖市的变量数据,房价(元/平方米)、建造成本(元/平方米)、土地成本(元/平方米)、人均可支配收入(元)和人口密度(人/平方公里)这些变量的数据来源是《中国统计年鉴》,利率数据来源是瑞斯金融数据库。需要注意的是, 用中长期(一至三年)贷款利率表示,
用中长期(一至三年)贷款利率表示,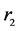 用个人住房公积金贷款利率(五年以上)表示,
用个人住房公积金贷款利率(五年以上)表示,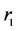 、
、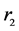 均为真实利率乘以100求得。由于原始数据存在明显的异方差问题,为此,本文取变量数据的自然对数值,有效缓解了异方差问题(见图3、图4)。
均为真实利率乘以100求得。由于原始数据存在明显的异方差问题,为此,本文取变量数据的自然对数值,有效缓解了异方差问题(见图3、图4)。
变量描述性统计见表1。

Figure 3. The scatter plot of hp and pi
图3. 房价关于人均可支配收入的散点图

Figure 4. The scatter plot of lnhp and lnpi
图4. 对数房价关于对数人均可支配收入的散点图
表1. 变量描述性统计
在回归前,还需对数据平稳性进行单位根检验。单位根检验包括同质面板和异质面板的单位根检验两类。前者主要有LLC检验(Levin、Lin和Chu,2002) [13] ;后者主要有LPS (Im、Pesaran和Shin,2003) [14] 、Fisher-ADF和Fisher-PP检验(Maddala和Wu,1999) [15] 。本文用这四种方法分别进行单位根检验,结果见表2。
由表2可知,所有变量一阶差分均为平稳,可进一步进行协整检验,判断变量之间是否存在长期均衡关系。协整检验结果见表3。
由表3可知,模型变量之间存在长期协整关系,因此可对房价模型进行回归。
3.1.2. 回归结果及分析
利用以上房价模型和变量数据,我们得到混合截面模型、随机效应模型、固定效应模型、差分模型回归结果如表4。
9有些学者在研究房价时,直接建立固定效应模型,这种做法是不准确的,模型是否选取适当需要根据模型的隐含假设是否成立来确定。
从表4中回归结果可知,建造成本、土地成本、人均可支配收入和人口密度这几个变量的系数符号与预期相符,均为正值,但系数的具体大小却大不相同,所以具体选择哪个模型还需进一步分析9。本文就以上四个模型的隐含假设分别作了检验,最后仅有差分模型通过了假设检验,所以本文最终选择了差分模型。
表2. 单位根检验
注:1) 括号内为P值;2) 原假设为“有单位根”;3) 估计方程包含截距项、时间趋势项和滞后项。
表3. 协整检验
注:1) 原假设为无协整关系;2) 估计方程含有截距项、时间趋势项和滞后项。
表4. 模型回归结果
注:1) 括号内是t统计值;2) *p < 0.05, **p < 0.01, ***p < 0.001。
在应用差分模型回归结果进行后续分析前,本文就模型可能存在的内生变量问题进行了处理。很多学者如刘琳(2003) [16] 、严金海(2006) [17] 、宋勃(2007) [18] 和况伟大(2012) [19] 认为土地成本与房价存在相互影响的关系,即土地成本这一解释变量在房价模型中是内生。本文就差分模型进行了内生性检验,检验结果表明模型确实存在内生性问题。综合考虑了工具变量的相关性以及外生性特点后,本文选取土地购置面积作为土地成本的工具变量。用工具变量的方法对差分模型进行回归,得到结果如下:
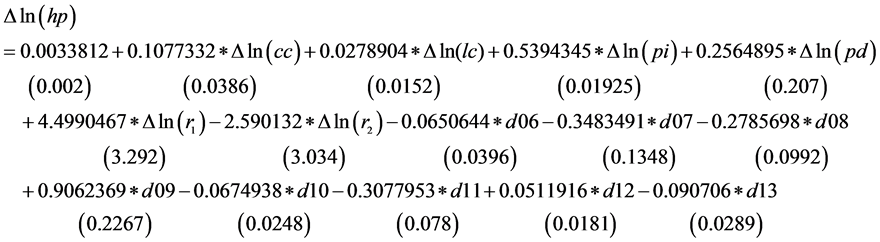
注: 表示时间二元变量,
表示时间二元变量, 对应2006年,以此类推。由于自由度的问题,
对应2006年,以此类推。由于自由度的问题,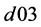 、
、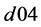 、
、 这几个二元变量未出现在模型回归结果中。
这几个二元变量未出现在模型回归结果中。
根据该回归结果,除了土地成本其他解释变量的系数符号均与预期相符。对于土地成本这一变量的系数与预期不符这一现象,本文给出以下解释:房地产项目建设周期一般长于一年,所以当年竣工的房屋中所包含的土地成本并不是来源于当年的土地购置费用,可能来源于一年前、两年前甚至更多年前购置土地所产生的费用,所以用当年的土地成本作为解释变量不是一个很合理的做法,这也是土地成本这一解释变量的系数符号与预期相悖的可能原因。为此,我们将土地成本这一解释变量用其一阶滞后项代替,重新进行回归,得到结果如下:
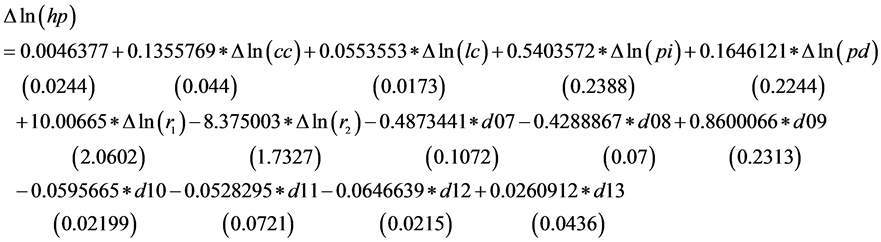
从这一回归结果来看,土地成本的一阶滞后项的系数为正,证实了之前的猜想是正确的。我们最关注的变量建造成本的系数约为0.14,这意味着其他变量保持不变的情况下,建造成本每增加1%,房价预期增加0.14%,这一系数在5%的显著性水平下显著。
至此可知建造成本对房价的边际影响,为了了解碳税对房价的影响,还需知道碳税对建造成本的影响,而这一影响程度依赖于碳税税率的大小,所以要首先确定碳税税率。
对于碳税税率的确定,从不同的角度考虑可能得到不同的结果。政府在制定碳税税率时,可能需要考虑对房价的影响,对民众福利的影响,对社会发展的影响,对技术进步的影响等。苏明等(2009) [20] 考虑了环境、经济、社会等方面的因素后,确定了碳税税率水平如表5。
根据表5可估算出2013年的碳税税率水平为13.75元/吨。根据雷中英(2011) [1] 的研究可知,新建一平米的房屋将会向大气中排放0.574吨CO2,即碳税的开征将会导致房屋建造成本增加7.8925元/平方米。根据《中国统计年鉴》可知2013年全国平均房屋建造成本为2643元/平方米,所以碳税开征将导致
表5. 碳税税率水平
建造成本预期增加0.2986%,将导致房价预期增加0.0418%。由此可见,其他因素不变的情况下,碳税的开征会导致房价预期增加0.0418%。
4. 结束语
二氧化碳大量排放所导致的温室效应问题越发引起全世界的关注,征收碳税来促进节能减排或许是一个比较好的解决措施。但是碳税的征收将导致二氧化碳高排放的建材行业以及房地产行业的成本增加,进而带来房价的上涨,进一步增加我国民众购房负担。所以,本文就碳税对房价可能造成的影响进行了前瞻性的研究。
本文建立理论模型,分析了消费者效用最大化行为以及房地产商利润最大化行为,最后得到结论1):碳税的征收会导致均衡房价的上涨以及均衡房屋交易量的减少。在此基础上,本文运用图示法对这一问题再次分析,验证了理论模型的结论。
进一步地,本文建立了房价模型来测算碳税对房价影响程度的大小,最后得到结论2):其他因素保持不变的情况下,碳税的开征会导致房价预期增加0.0418%。
根据结论1)可知,碳税的开征导致了均衡房屋交易量的减少,即能在一定程度上促进房地产行业减少碳排放。根据结论2)可知,碳税政策并不会给房地产行业造成很大影响,即很大程度上并不会抬高房价。综合以上两条结论,本文认为对房地产行业征收碳税是合理可行的。
致谢
在本次论文的撰写中,我们得到了王明喜教授的悉心指导。从题目的选择一直到论文的最终完成,王老师始终都给予我们耐心的帮助和不懈的支持。在此谨向王老师致以诚挚的谢意和崇高的敬意。此外,本次论文还得到了阳和平教授和潘红宇教授的大力支持,在此一并表示感谢。
NOTES
2即房价是用实际价格而不是名义价格表示的。
3况伟大(2011)研究房产税对房价影响时使用了类似的效用函数,但考虑到自然对数函数的性质,本文在其基础上作了修改。