1. 引言
铜氧化物高温超导体属于典型的低维(二维)强关联电子系统,对其正常态性质和非常规超导机理的理解是当今凝聚态物理领域的一个难题。人们普遍认为该类材料的物理行为可以根据掺杂的莫特(Mott)绝缘体来加以描述。随着掺杂载流子性质(空穴或者电子)和浓度的变化,铜氧化物高温超导体中存在电荷和自旋自由度的相互竞争、多种不同的长程和短程自旋关联、电荷有序、以及d波超导电性等复杂的相图。近年来,中子散射、角分辨光电子谱、扫描隧道显微镜等大量的实验研究发现铜氧化物高温超导体呈现出纳米尺度的非均匀特性[1] ,包括条纹电荷序[2] 、棋盘电荷序[3] 、非公度电荷序[4] 等。这些实验结果表明澄清纳米尺度的电子态对于理解铜氧化物高温超导体的物理特性具有重要的意义。由于四方哈伯德团簇(图1实线围成的正方形)是构成CuO2平面(由图1所示点线连接而成)的基本结构单元,因而研究其自旋和电荷关联特征有助于理解铜氧化物高温超导体在纳米尺度的电子态[5] 。
A.N. Kocharian等人在考虑图1所示近邻电子跃迁t和在位哈伯德U的情况下,研究了四方哈伯德团簇的自旋-电荷分离、相分离、电子配对涨落、以及赝能隙等物理特性[6] - [11] 。研究结果表明当平均电子数 且U小于临界值Uc = 4.584 t时,电子趋于形成配对状态,并导致出现
且U小于临界值Uc = 4.584 t时,电子趋于形成配对状态,并导致出现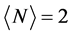 和
和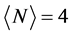 的相分离状态;而当U大于Uc时,体系趋于形成自旋–电荷分离的莫特–哈伯德绝缘态。他们的研究结果不仅证实关联电子系统在纳米尺度上表现出复杂的物理行为,而且成功地解释了铜氧化物高温超导体中观测到的重要实验现象。
的相分离状态;而当U大于Uc时,体系趋于形成自旋–电荷分离的莫特–哈伯德绝缘态。他们的研究结果不仅证实关联电子系统在纳米尺度上表现出复杂的物理行为,而且成功地解释了铜氧化物高温超导体中观测到的重要实验现象。
在铜氧化物高温超导体中,次近邻格点间电子跃迁 (或者称为对角跃迁,如图1所示)对其磁性和d波超导特性具有重要的影响。我们前期关于二维哈伯德模型的量子蒙特卡罗模拟结果发现
(或者称为对角跃迁,如图1所示)对其磁性和d波超导特性具有重要的影响。我们前期关于二维哈伯德模型的量子蒙特卡罗模拟结果发现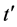 抑制了反铁磁自旋涨落[12] 。此外,大量的理论研究结果表明近邻库仑相互作用V对多电子体系的电荷和自旋关联、以及电子配对态等同样具有重要的影响。例如,Onari等人对二维扩展哈伯德模型的研究发现V将引起电荷涨落的增强,从而使得电子配对的对称性发生改变,而且在
抑制了反铁磁自旋涨落[12] 。此外,大量的理论研究结果表明近邻库仑相互作用V对多电子体系的电荷和自旋关联、以及电子配对态等同样具有重要的影响。例如,Onari等人对二维扩展哈伯德模型的研究发现V将引起电荷涨落的增强,从而使得电子配对的对称性发生改变,而且在 时甚至导致电荷密度波的出现[13] 。
时甚至导致电荷密度波的出现[13] 。

Figure 1. Square Hubbard clusters and the connected CuO2 plane
图1. 四方哈伯德团簇及其连接而成的CuO2平面
为了进一步理解铜氧化物高温超导体在纳米尺度上的物理特性,本文采用数值精确对角化方法系统地研究了四方哈伯德团簇中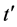 和V对电子对束缚能、自旋和电荷能隙、及其对应跨越温度的物理影响。
和V对电子对束缚能、自旋和电荷能隙、及其对应跨越温度的物理影响。
2. 模型和物理量
我们研究的四方哈伯德团簇如图1中实线围成的正方形所示,其哈密顿量表达为:
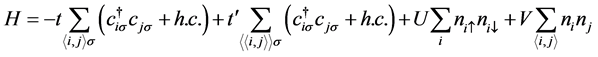 (1)
(1)
这里 和
和 分别代表近邻和次近邻的一对格点
分别代表近邻和次近邻的一对格点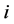 与
与 ,并约定每对只求和一次,也即描述从格点
,并约定每对只求和一次,也即描述从格点 向格点
向格点 的跃迁,
的跃迁, 向
向 的跃迁用它的厄米共轭
的跃迁用它的厄米共轭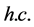 表示。
表示。 和
和 分别表示近邻和次近邻跃迁积分,
分别表示近邻和次近邻跃迁积分,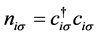 表示自旋为
表示自旋为 电子密度算符,
电子密度算符,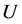 和
和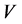 分别表示在位哈伯德与近邻库仑相互作用强度。本文中我们取近邻跃迁积分
分别表示在位哈伯德与近邻库仑相互作用强度。本文中我们取近邻跃迁积分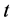 作为能量单位。
作为能量单位。
在铜氧化物高温超导体中,自旋和电荷之间的相互竞争、多种竞争序、以及超导状态出现在靠近电子半填充的低掺杂区域,因而我们将集中分析当平均电子数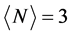 (对应于在
(对应于在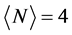 的半填充系统中加入一个空穴)时四方哈伯德团簇的物理特性。为了考察加入的空穴是否形成配对状态,我们定义如下的电子对束缚能:
的半填充系统中加入一个空穴)时四方哈伯德团簇的物理特性。为了考察加入的空穴是否形成配对状态,我们定义如下的电子对束缚能:
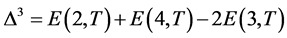 (2)
(2)
式中 表示平均电子数为N温度为T时系统的总能量。当电子对束缚能
表示平均电子数为N温度为T时系统的总能量。当电子对束缚能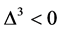 时,加入的空穴易于形成配对状态,同时平均电子数
时,加入的空穴易于形成配对状态,同时平均电子数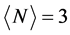 的体系趋于相分离为
的体系趋于相分离为 (半填充)和
(半填充)和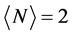 (加入两个空穴)的非均匀分布状态,相应于图1中不同的四方团簇具有不同的电子数。
(加入两个空穴)的非均匀分布状态,相应于图1中不同的四方团簇具有不同的电子数。
定义有限温度下的化学势如下[6] :
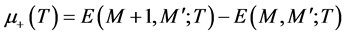 (3)
(3)
 (4)
(4)
式中 表示上下电子分别 为
表示上下电子分别 为 和
和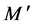 时的系统总能量,
时的系统总能量,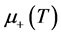 和
和 代表体系电子数为
代表体系电子数为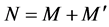 时,增加或者减少一个电子所需要的最低能量。对于我们研究的情况,
时,增加或者减少一个电子所需要的最低能量。对于我们研究的情况,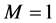 ,
,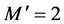 ,
, 。注意公式(1)采用的是巨正则系综、而公式(3)和(4)采用的是正则系综。根据上述两个化学势,电荷能隙可以表示为[6] :
。注意公式(1)采用的是巨正则系综、而公式(3)和(4)采用的是正则系综。根据上述两个化学势,电荷能隙可以表示为[6] :
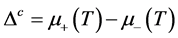 (5)
(5)
与电荷能隙相类似,在一定温度下,我们定义自旋能隙为两种不同自旋位形的能量差[6] :
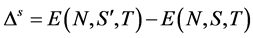 (6)
(6)
这里,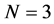 ,
,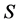 和
和 分别对应于体系处于最低能量状态和第一激发态的总自旋值。
分别对应于体系处于最低能量状态和第一激发态的总自旋值。
3. 计算结果和讨论分析
我们首先考察对角跃迁t'和近邻库仑相互作用V对电子配对的影响。由图2(a)可以看出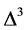 为负值对应的最大Uc随着
为负值对应的最大Uc随着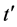 的增加逐渐向右移动,导致电子配对的U值区间不断扩大,而且当U > 1.5时,
的增加逐渐向右移动,导致电子配对的U值区间不断扩大,而且当U > 1.5时,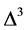 随着
随着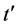 的增加逐渐降低。由图2(b)可以看出
的增加逐渐降低。由图2(b)可以看出 为负值对应的最小Uo和最大Uc随着V的增加分别向右和向左移动,导致电子配对的U值区间缩小,而且在整个U值区间,
为负值对应的最小Uo和最大Uc随着V的增加分别向右和向左移动,导致电子配对的U值区间缩小,而且在整个U值区间,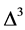 随着V的增加逐渐升高。我们还发现当V > 0.05时,在整个U值区间
随着V的增加逐渐升高。我们还发现当V > 0.05时,在整个U值区间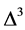 皆为正值。图2(a)和图2(b)表明
皆为正值。图2(a)和图2(b)表明 有利于电子形成配对态,而V将显著抑制电子形成配对态。图2(c)和图2(d)分别表示
有利于电子形成配对态,而V将显著抑制电子形成配对态。图2(c)和图2(d)分别表示 = 0.2和V = 0.04时,温度对电子对束缚能的影响,从中可以看到,当U < 4.0时,电子对束缚能随着温度的升高而增加,表明电子配对受到热涨落的削弱。
= 0.2和V = 0.04时,温度对电子对束缚能的影响,从中可以看到,当U < 4.0时,电子对束缚能随着温度的升高而增加,表明电子配对受到热涨落的削弱。
图3表示温度T = 0.001、对角跃迁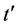 取不同值时,自旋和电荷能隙随U的变化关系,其中Uc代表电荷能隙由负变正对应的临界哈伯德相互作用强度。在
取不同值时,自旋和电荷能隙随U的变化关系,其中Uc代表电荷能隙由负变正对应的临界哈伯德相互作用强度。在 区间,负的电荷能隙意味着电子形成配对状态,正的自旋能隙意味着配对电子处于总自旋为0的自旋单重态。当
区间,负的电荷能隙意味着电子形成配对状态,正的自旋能隙意味着配对电子处于总自旋为0的自旋单重态。当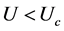 时,我们发现自旋能隙与电荷能隙的绝对值相等,即
时,我们发现自旋能隙与电荷能隙的绝对值相等,即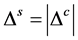 。该行为与U取负值(相互吸引哈伯德模型)时的结果类似,表明电子间形成相干配对,从而容易产生超导状态。而当
。该行为与U取负值(相互吸引哈伯德模型)时的结果类似,表明电子间形成相干配对,从而容易产生超导状态。而当 时,四方哈伯德团簇处于
时,四方哈伯德团簇处于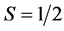 的未饱和铁磁态,正的
的未饱和铁磁态,正的 和
和 表示在
表示在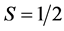 和
和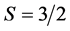 态之间存在自旋能隙,且单粒子激发需要提供有限能量,因而该区域可以称为自旋液体态。由图3可以发现,从
态之间存在自旋能隙,且单粒子激发需要提供有限能量,因而该区域可以称为自旋液体态。由图3可以发现,从 增加到
增加到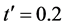 的过程中,
的过程中,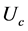 随着
随着 的增大而增大,表明
的增大而增大,表明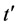 扩展了电子配对的U值区间。
扩展了电子配对的U值区间。

Figure 2. Curve: The electron pair binding energy as a function of U. (a) and (b) correspond to different t' or V at T = 0.001. (c) t' = 0.2, T = 0.001 and 0.05; (d) V = 0.04, T = 0.001 and 0.05
图2. 电子对束缚能随哈伯德U的演化曲线。(a)和(b)分别对应于温度T = 0.001,t'或者V取不同值;(c) t' = 0.2, T = 0.001和0.05;(d) V = 0.04, T = 0.001和0.05
图4表示温度T = 0.001、近邻库仑相互作用V取不同值时,自旋和电荷能隙随U的变化关系,其中Uo和Uc代表电荷能隙取负值对应的最小和最大临界哈伯德相互作用强度。与图3类似,在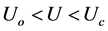 区间,电子间形成相干配对状态,而当
区间,电子间形成相干配对状态,而当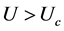 时,四方哈伯德团簇处于自旋液体态。当
时,四方哈伯德团簇处于自旋液体态。当 时,零自旋能隙和有限电荷能隙表明系统处于哈伯德-莫特绝缘体状态。由图4还可以发现,从
时,零自旋能隙和有限电荷能隙表明系统处于哈伯德-莫特绝缘体状态。由图4还可以发现,从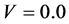 增加到
增加到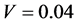
的过程中,Uo随着V的增大向右移动,而且 随着V的增大却向左移动,表明V显著缩小了电子配对的U值区间。
随着V的增大却向左移动,表明V显著缩小了电子配对的U值区间。
对于一个无相互作用多电子体系,电子的电荷和自旋激发具有相似的特征,即不产生自旋–电荷分离。然而在相互作用系统中,情况会有所不同,电子的电荷自由度可能会与它的自旋自由度产生分离。图5给出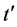 取不同值时的T-U相图。图中Fermi liquid, MH insulator,charge pairing,和spin pairing分别代表费米液体,莫特–哈伯德绝缘体、电荷配对、以及自旋配对相.电荷配对临界温度
取不同值时的T-U相图。图中Fermi liquid, MH insulator,charge pairing,和spin pairing分别代表费米液体,莫特–哈伯德绝缘体、电荷配对、以及自旋配对相.电荷配对临界温度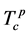 和自旋配对临界温度
和自旋配对临界温度 可以从相应的能隙为零条件(
可以从相应的能隙为零条件(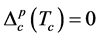 和
和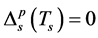 )得出,而金属–绝缘体转变温度Tc同样根据电荷能隙为零的条件给出。在费米液体区,自旋和电荷能隙皆为零,而在莫特–哈伯德绝缘体区,系统处于电荷能隙有限但自旋能隙为零的自旋–电荷分离态。在温度低于
)得出,而金属–绝缘体转变温度Tc同样根据电荷能隙为零的条件给出。在费米液体区,自旋和电荷能隙皆为零,而在莫特–哈伯德绝缘体区,系统处于电荷能隙有限但自旋能隙为零的自旋–电荷分离态。在温度低于 而高于
而高于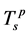 时,电荷形成配对而自旋能隙为零,表明系统处于自旋–电荷分离态。在临界温度
时,电荷形成配对而自旋能隙为零,表明系统处于自旋–电荷分离态。在临界温度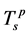 以下,电荷配对与自旋配对同时形成,即自旋和电荷自由度同时发生凝聚,从而可以导致图1中CuO2平面内超导态的形成。由图5可以发现,
以下,电荷配对与自旋配对同时形成,即自旋和电荷自由度同时发生凝聚,从而可以导致图1中CuO2平面内超导态的形成。由图5可以发现,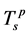 曲线随着
曲线随着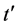 的增加扩展到更大的Uc,且在同一U值
的增加扩展到更大的Uc,且在同一U值 随着
随着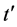 的增加而升高,该结果进一步证明
的增加而升高,该结果进一步证明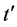 有助于形成电子配对的超导态。
有助于形成电子配对的超导态。
图6给出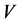 取不同值时的T-U相图。图中各相与图5给出的结果相同,电荷配对临界温度
取不同值时的T-U相图。图中各相与图5给出的结果相同,电荷配对临界温度 和自旋配对临界温度
和自旋配对临界温度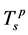 ,以及金属–绝缘体转变温度Tc同样根据电荷和自旋能隙为零的条件给出。从图6可以看出,随着V的增大,电荷配对及自旋配对相应的U值区域急剧缩小,且在同一U值
,以及金属–绝缘体转变温度Tc同样根据电荷和自旋能隙为零的条件给出。从图6可以看出,随着V的增大,电荷配对及自旋配对相应的U值区域急剧缩小,且在同一U值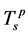 随着V的增加而迅速降低,该结果进一步证明V对超导态具有显著的抑制作用。我们还发现,当
随着V的增加而迅速降低,该结果进一步证明V对超导态具有显著的抑制作用。我们还发现,当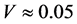 时,自旋能隙区将从相图中消失,表明系统不能形成稳定的电子配对态。
时,自旋能隙区将从相图中消失,表明系统不能形成稳定的电子配对态。
4. 结论
为了深入理解铜氧化物高温超导体在纳米尺度的电子态性质,我们采用数值精确对角化方法研究了

Figure 5. Curve: T-U phase diagram at t' = 0.0, 0.1, 0.2. The curves with filled-symbols, open-symbols, and without symbols represent the boundaries of charge pairing, spin pairing, and metal-insulator transition, respectively. Uc denotes the maximum U with spin pairing
图5. t' = 0.0, 0.1, 0.2时对应的T-U相图。实心符号、空心符号、无符号曲线分别代表电荷配对、自旋配对、以及金属-绝缘体转变的相边界。Uc代表自旋配对的最大U值
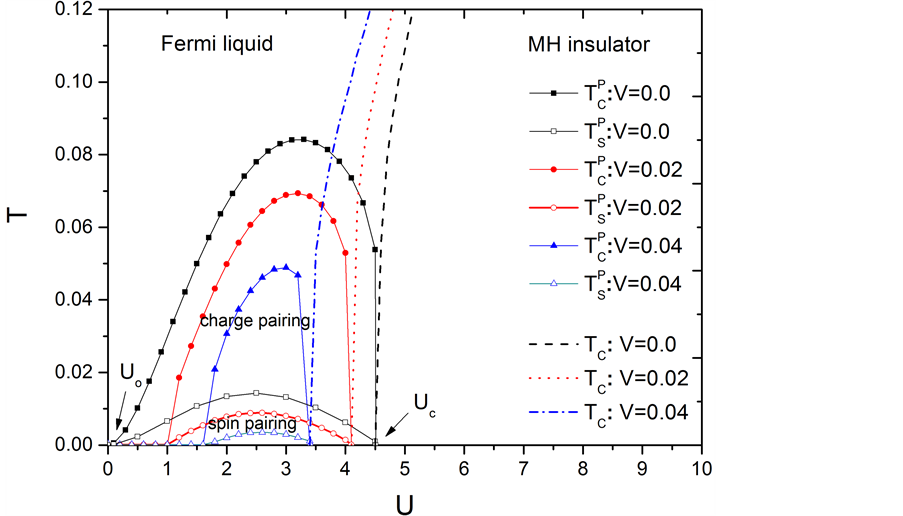
Figure 6. Curve: T-U phase diagram at V = 0.0, 0.02, 0.04. The curves with filled-symbols, open-symbols, and without symbols represent the boundaries of charge pairing, spin pairing, and metal-insulator transition, respectively. Uo and Uc denote the minimum and maximum U with spin pairing
图6. V = 0.0, 0.02, 0.04时对应的T-U相图。实心符号、空心符号、无符号曲线分别代表电荷配对、自旋配对、以及金属–绝缘体转变的相边界。Uo和Uc代表自旋配对的最小和最大U值
四方哈伯德团簇中对角跃迁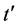 和近邻库仑相互作用V对电子对束缚能、自旋和电荷能隙及其对应跨越温度的物理影响。我们考察了系统在低温T = 0.001和有限温度下,且平均电子数
和近邻库仑相互作用V对电子对束缚能、自旋和电荷能隙及其对应跨越温度的物理影响。我们考察了系统在低温T = 0.001和有限温度下,且平均电子数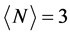 时的电子配对、自旋和电荷配对等物理特征。研究结果表明对角跃迁t'有利于形成电子配对的超导态,而近邻库仑相互作用V将显著抑制超导态的形成。我们的研究结果对于理解铜氧化物高温超导体的物理特性具有重要的意义。
时的电子配对、自旋和电荷配对等物理特征。研究结果表明对角跃迁t'有利于形成电子配对的超导态,而近邻库仑相互作用V将显著抑制超导态的形成。我们的研究结果对于理解铜氧化物高温超导体的物理特性具有重要的意义。
基金项目
国家自然科学基金(批准号:11174072,91221103)资助的课题。