1. 引言
谐波和间谐波测量是谐波问题的一个重要分支,也是分析和治理谐波问题的出发点和主要依据[1] 。随着电力电子技术的日益发展,以及非线性负荷的接入,在给电网注入谐波的同时,也注入了大量间谐波。间谐波的存在带来电网波形过零点偏移和闪变等新的问题,其高精度的检测越来越受到学者们的关注。目前对间谐波的检测方法主要有:快速傅里叶变换法、Prony方法、改进型支持向量机(SVM)算法和小波变换法等 [2] [3] 。傅里叶要求分析窗宽度为各个频率信号周期的公倍数,才可得到精确的信号频谱,Prony方法对噪声比较敏感需要先进行消噪 [4] ,改进型支持向量机(SVM)算法改进的是利用函数拟合来检测间谐波,能准确地检测出电力系统间谐波的频率,但是检测范围和精度都受预设模型影响,而且在小样本条件下幅值误差较大。由于小波变换具有时–频窗口可以自适应变化的特点,不但可以分析稳态信号,也可以分析非平稳信号的优点,已经成为电力系统谐波检测中新的研究方向 [5] - [9] 。
基于Mallat算法的小波多分辨分析将信号按一定的尺度进行划分,不同频率的信号被划分到不同的频段中,然后对各子频段进行重构,从而分离出各频段谐波信息。Mallat算法对信号频带划分并不是均匀的,而是高频部分宽而低频部分窄,所以在信号的多分辨率分析中,信号的低频部分能够得到精确的分解,但高频段频率相近的谐波分量难以分离 [5] - [10] 。
本文在对信号进行小波变换之前,利用正弦和余弦函数对信号调制得到调制后的信号,改变了信号的频率结构,调制后的信号包含直流分量和其他频率分量两部分,而我们需要的信号包含在直流分量中,然后再利用基于Mallat的多分辨分析提取调制后信号的直流分量,滤除其他频率分量,相比直接利用小波变换对原始信号处理,这样能够很好的利用多分辨分析中低频频率分辨率高,并且经过调制后分离出的直流分量,能够直接用于计算对应的谐波和间谐波幅值相位。经过MATLAB实例仿真验证,该方法在解决小波变换在高频段频率分辨率低缺点下,能够准确检测谐波和间谐波分量。
2. 基于小波变换的谐波检测算法
2.1. 基于Mallat的多分辨率分析
基于MATLAB快速算法的谐波提取方法是目前应用较为广泛的谐波检测方法。其基本原理如下[11] :
分解算法为
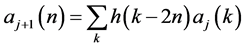 (1)
(1)
 (2)
(2)
h和g分别是选定小波基函数以及尺度函数所生成的低通和高通滤波器。 称为离散逼近信号,它描述了信号的低频部分信息,
称为离散逼近信号,它描述了信号的低频部分信息, 称为离散细节信号,它描述了信号的高频部分信息。
称为离散细节信号,它描述了信号的高频部分信息。
而重构公式为
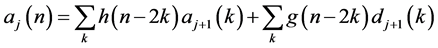 (3)
(3)
小波函数和尺度函数之间存在如下关系
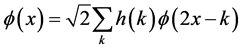 (4)
(4)
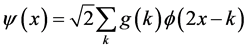 (5)
(5)
小波的多分辨率分析将信号按一定的尺度进行划分,不同频率的信号被划分到不同的频段中,然后对各子频段进行重构,从而分离出各频段谐波(如图1)。
2.2. 谐波检测分析
设电流信号为 ,如式中
,如式中
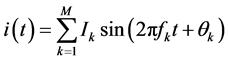 (6)
(6)
式中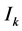 、
、 和
和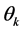 分别表示谐波幅值、频率和相位角,M是最高次谐波阶数。
分别表示谐波幅值、频率和相位角,M是最高次谐波阶数。
设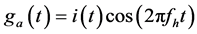 ,
,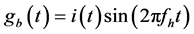 ,其中
,其中
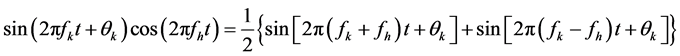 (7)
(7)
 (8)
(8)
当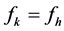 时,整理式(3-2)和式(3-3),得到
时,整理式(3-2)和式(3-3),得到
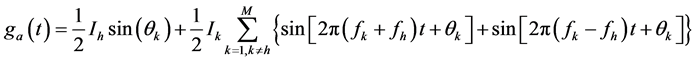 (9)
(9)
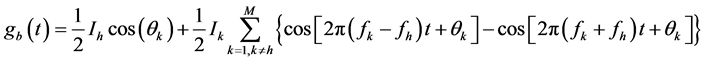 (10)
(10)
从式(9)中可以看出调制后信号包含直流分量 和其他频率分量,式(10)中可以看出调制后信号包含直流分量
和其他频率分量,式(10)中可以看出调制后信号包含直流分量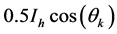 和其他频率分量,传统的fourier变换实际上是对调制后信号
和其他频率分量,传统的fourier变换实际上是对调制后信号 ,
, 进行周期内的积分,如式
进行周期内的积分,如式
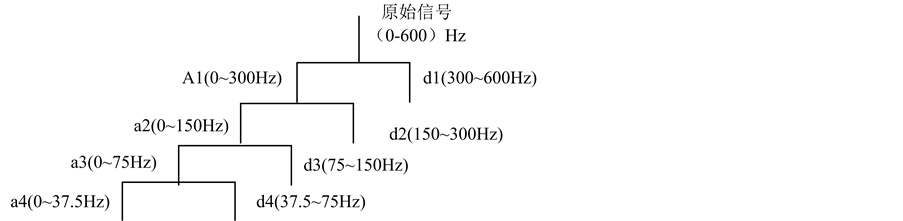
Figure 1. Exploded view of the multi-resolution analysis
图1. 多分辨率分析分解示意图
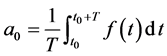 (11)
(11)
 (12)
(12)
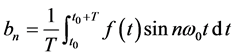 (13)
(13)
式中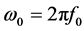 ,而谐波的幅值与相位信息可以由
,而谐波的幅值与相位信息可以由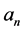 ,
, 计算得到,而积分的作用是保留了需要检测的频率分量信息,其他频率分量经过周期内的积分后都被消除了,这样做的好处是能够准确的得到各次谐波分量信息,然而由于积分的存在,使得信号缺乏时域信息,并且因为必须是在周期内的积分才能消除调制后除直流分量外的其他频率分量,当信号所含频率分量除了含信号基波频率整数倍外,还有其他非整数倍频率时,即间谐波,在周期内积分使fourier难以检测含间谐波信号,并且丢失了信号的时域信息。
计算得到,而积分的作用是保留了需要检测的频率分量信息,其他频率分量经过周期内的积分后都被消除了,这样做的好处是能够准确的得到各次谐波分量信息,然而由于积分的存在,使得信号缺乏时域信息,并且因为必须是在周期内的积分才能消除调制后除直流分量外的其他频率分量,当信号所含频率分量除了含信号基波频率整数倍外,还有其他非整数倍频率时,即间谐波,在周期内积分使fourier难以检测含间谐波信号,并且丢失了信号的时域信息。
前面介绍了基于Mallat的多分辨率分析能够对信号进行有效的分频,然后利用基于Mallat的多分辨率分析对调制后的信号进行分频,得到调制后信号的直流分量。那么对Ik计算可以转化为对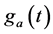 的直流分量
的直流分量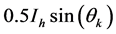 ,
,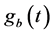 的直流分量
的直流分量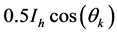 的提取,这样利用小波变换频带划分,提取的直流分量不但保留了时域信息,而且还能检测含间谐波信号,电力系统电网侧谐波参数Ik的计算如式(14)。
的提取,这样利用小波变换频带划分,提取的直流分量不但保留了时域信息,而且还能检测含间谐波信号,电力系统电网侧谐波参数Ik的计算如式(14)。
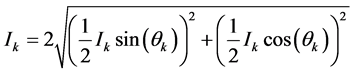 (14)
(14)
相位角
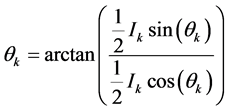 (15)
(15)
3. 电网的间谐波仿真分析
假定信号为
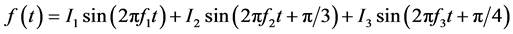 (16)
(16)
频率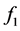 、
、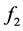 和
和 分别取50Hz、175.5Hz、450Hz,对应的幅值分别为
分别取50Hz、175.5Hz、450Hz,对应的幅值分别为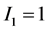 、
、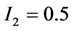 、
、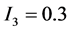 ,其中50 Hz为基波分量,450 Hz为9次谐波分量,175.5 Hz为信号所含的间谐波成份。
,其中50 Hz为基波分量,450 Hz为9次谐波分量,175.5 Hz为信号所含的间谐波成份。
采用2.2对信号的分析方法,将需要检测的频率调制后,转换为对调制后信号直流分量的检测,然后利用基于Mallat算法的多分辨分析,选用db44小波基函数小波变换的滤波器基本组件。
设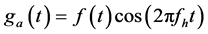 ,
,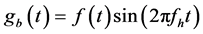 ,当
,当 时
时
按照式(9)和式(10)可知调制后的信号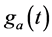 和
和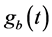 中包含的频率成份
中包含的频率成份 ,
,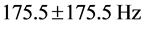 、
、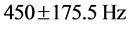 ,并且我们需要的信息就是调制后信号的直流分量,即
,并且我们需要的信息就是调制后信号的直流分量,即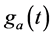 中的
中的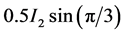 和
和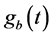 中的
中的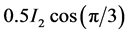 ,然后利用基于Mallat算法的多分辨分析将
,然后利用基于Mallat算法的多分辨分析将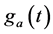 中的
中的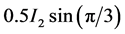 和
和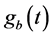 中的
中的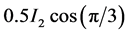 从
从 和
和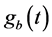 提取出来。信号的175.5 Hz的谐波分量幅值和相位计算如式(14)和式(15)。
提取出来。信号的175.5 Hz的谐波分量幅值和相位计算如式(14)和式(15)。
在进行谐波分析时,以采样频率1200 Hz对信号进行采样,并取1024个采样数据点为一组进行谐波分析。根据采样定律,能检测到的最大频率为600 Hz。按照式(17)确定分解层数
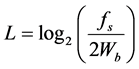 (17)
(17)
式中fs和Wb分别是采样频率和最低频率分辨率,从电网谐波分析中可以知道信号调制后得到的调制信号ga(t),gb(t)所含的最低频率为125.5 Hz,为了分离直流分量,最低频带宽度必须低于125.5 Hz,为了减少频带混叠的影响,这里选择Wb = 75 Hz,故分解层数为3层。
对信号分别作余弦和正弦调制后得到的如图3(a)和图4(a)所示,原始信号如图2所示。用基于Mallat算法的多分辨分析对调制后的信号分解,得到的各层逼近部分如图3(b)和图4(b),因为采样频率为1200 Hz,信号调制后所含的最低频率是125.5 Hz,而我们需要的是调制后信号的直流分量,故分解后我们需要的直流分量在逼近部分的a3中,这一点也可以在图1中得到,因为a3所含的频率范围是0~75 Hz,d3所含的频率范围是75~150 Hz,125.5 Hz的频率分量在d4中,125.5是信号调制后所含的最低频率,其他更高的频率分量更加不会出现在a3中,但从图3(b)和图4(b)的a3所示波形并不是一条直线,这是因为小波变换存在的频率混叠造成的,而且MATLAB的小波变换工具对信号分解前会对信号做一个周期延拓的预处理,这也就是为什么a3两边会有一定的波动,并不是理论上的直流分量,为了减少这种误差,本文对图3(b)和图4(b)中a3所示的含少了其它非直流分量做均值处理,得到图3(b)中a3的均值为0.2173,图4(b)中a3的均值为0.1249,故175.5 Hz出信号的谐波分量幅值为0.5013,相位为60.1138˚。
其它频率分量的检测方法类似,检测结果如表1。
 (a)
(a) (b)
(b)
Figure 3. (a) After the signal is modulated by the cosine; (b) Modulated by a cosine signal layers approximation section
图3. (a) 信号经余弦调制后;b) 信号经余弦调制后的各层逼近部分
 (a)
(a)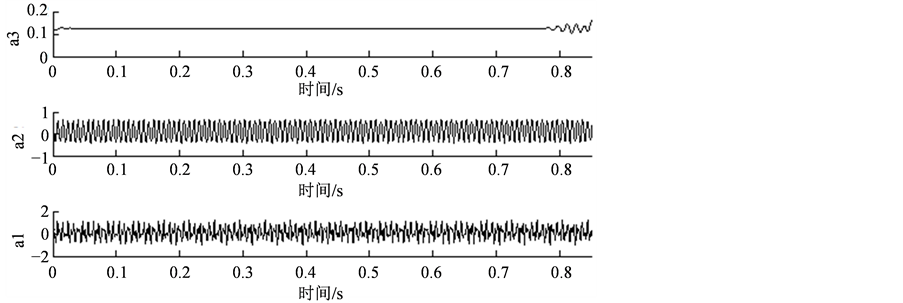 (b)
(b)
Figure 4. (a) After the signal is modulated by the sinusoidal; (b) Modulated by a sinusoidal signal layers approximation section
图4. (a) 信号经正弦调制后;(b) 信号经正弦调制后的各层逼近部分

Table 1. Harmonic component test results
表1. 谐波分量检测结果
4. 结论
本文利用小波变换频率划分能力,利用正弦和余弦函数对原始信号调制,改变原始信号的频率结构,再利用基于Mallat的多分辨分析提取调制后信号的直流分量,用于计算原始信号对应的谐波分量幅值与相位。利用基于Mallat的多分辨分析在低频分辨率高优点,避免多个频率分量被划分在同一个频段内,降低了采样要求,并不需要采样整周期数据。由于小波变换的频率混叠现象,使得在计算时存在一定的误差,所以今后工作需要提出更好的方法消除或则抑制频率混叠,或则找到一种更好的调制函数,使得需要检测的谐波分量调制低频段,而其他不需要的频率分量则远离这一频段,这样也能很好的减少频率混叠的影响。随着小波变换的不断发展和完善,小波变换在谐波检测分析的优势会越加明显。