1. 引言
近年来，多机器人路径规划已成为机器人领域中的一个热点问题。根据机器人对环境的了解程度，可以分为两种类型：环境信息完全已知的全局规划和环境信息完全未知或部分未知的局部路径规划[1] [2] 。多机器人路径规划是为均处在同一个简单或复杂，静态或动态，已知或未知的工作空间中的每个机器人找到一条路径，能避开障碍物并能保证机器人之间无碰撞，最后以最小或较小的消耗完成自己的任务[3] [4] 。由于多个机器人间存在资源竞争、且共处一个工作空间，这就造成了机器人间的冲突，解决机器人间的冲突已成为多机器人系统要解决的关键问题。
解决路径规划冲突问题，已有众多学者使用众多方法做了多年的深入研究并产生了大量研究成果[5] -[7] 。已有的研究解决方法大致可以分为集中式和离散式两类。集中式方法是将所有的机器人当作一个整体进行路径优化，但在不同的环境下优化结果不可靠，特别是对于部分可知的MDP环境或者机器人太多的环境。离散式方法是分别对单个的机器人进行路径优化，并随时解决优化过程中出现的冲突。两种方法共同的缺陷是算法的计算时间太长，仅能用于较小的环境，且不能保证在较短的时间内总是获得优化或接近优化的结果。
基于上述分析，本文提出采用基于XCS的离散启发式方法用于机器人的路径规划，机器人的优先权由其XCS的预测回报值来确定，而由集中式高水平的规划机器人动态分配各机器人的优先顺序，以解决机器人间的冲突，共同完成多机器人系统的路径规划。
2. 相关技术原理
2.1. Q学习
Q学习是由
1989年提出的基于
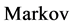环境的一种学习算法(MDP) [8] 。其原理是通过对感知的环境状态采取各种试探动作，获得此种试探动作对此种环境状态的奖励或者惩罚信号，并能不断调整学习策略以获得较大的奖励或较小的惩罚，同时反馈给其它机器人，并能够保证学习的收敛性。
单机器人的学习环境是基于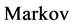
提出的有限四元组
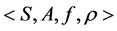，其中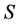
是有限环境状态集，
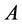为机器人有限动作集，
为状态转换概率函数。
为机器人的回报函数。
多机器人的学习环境是基于MR-MDP，是一个随机的四元组
。
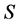为离散的环境状态集、
为作用于机器人的动作集，
，
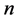为机器人数量。
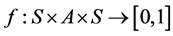为状态转换概率函数。
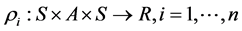为机器人的回报函数。在多机器人系统，状态转换是所有机器人联合行动的结果，
，
，
。
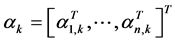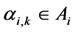2.2. 学习分类器(Accuracy-Based Learning Classifier System, XCS)
XCS [9] 作为LCS的衍生系统是由Wilson提出的基于精度的学习分类器，集成了强化学习、遗传算法和覆盖算法。XCS是由条件、动作和预测回报三个主要的参数组成：条件指明XCS可以匹配的环境输入状态；动作表示在该XCS匹配的环境状态下XCS的建议动作；预测回报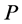
表示该XCS被匹配且执行了该XCS所建议的动作后系统预期从环境获得的回报。预测误差
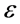表示预测回报
的误差；适应强度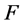
表示预测回报
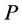的精度。
Step 1：在开始随机分类器集合选择动作概率大的动作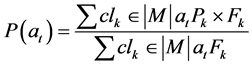
作用于环境，根
据环境输入，产生一个匹配环境输入的匹配规则集，然后依据每个分类器的回报预测和适应强度值，生成整个系统的预测列表和动作集。
Step 2：分类器在执行机制过程中，每选择一个动作
作用于环境，分类器从环境获得一个回报
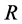，回报预测、分类器适应值强度更新如下：
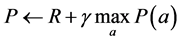(1)
其中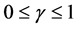
是学习效率。
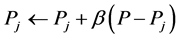(2)
(3)
(4)
(5)
其中参数
控制预测误差
的冗余度；参数
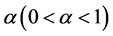和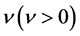
是常量，控制当
被超过时精确度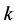
的下降速度。动作集中的绝对精确度值
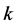被转换为相对精确度值
，XCS的适应度值
是依据相对精确度值进行更新：
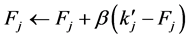(6)
Step 3：当匹配规则集中没有分类器与环境输入信息相匹配时，启动规则发现机制的覆盖算法，随机产生一个分类器。覆盖算法产生的新规则的条件部分与环境信息匹配，该规则淘汰规则集中强度最小的规则，存入规则集中。
Step 4：未达到设定迭代次数转Step 2。
3. 基于XCS的多机器人路径规划冲突解决方案
3.1. 多机器人学习训练方法
在基于XCS的多机器人路径规划冲突解决方案中，机器人学习训练分为个体和团队训练两种方法。在个体训练阶段，XCS使机器人学会避碰，确保机器人在安全的情况下向设定目标运动。在团队训练阶段，团队训练引入的机器人管理者决定机器人的优先权，在任一时刻，所有机器人在没有考虑其他机器人位置的情况下预先感知环境，然后以机器人在管理者约束下的成功等级概率作为各机器人优先权，各机器人依优先权大小进行下一步的行动。
3.2. 机器人优先级别设计
多机器人在未到达目标位置前，个体机器人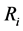
在区域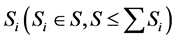
内移动。如果在时刻
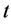，机器人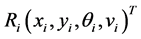
对目标位置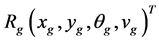
进行预测，计算出自己预接近到目标的理想速度和方位角，并将结果通过无线网络发布给其他机器人，同时自己升级为领导机器人。其他机器人根据收到的信息计算出自己的位置和运动趋势，并同时计算出目标和其他机器人与自身的相对位置，根据其他机器人的情况，提出自己预接近目标的理想速度和方位角。对于最终的等级方案，领导机器人采用成功概率加权的方法。该方法首先建立如下位置估计方程：
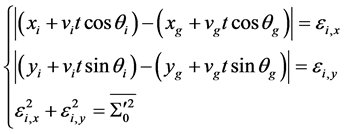(7)
其中：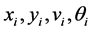
分别为成员机器人位置、预计速度和方位角；
为机器人目标位置、速度和方向；
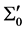为对目标机器人的移动安全半径(根据机器人大小等因素设定的经验值)；
和
为二维分量上的偏差。
将领导机器人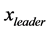
，
，
，
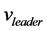代入上式，并将求得的
代入下式，由此可得各成员机器人在机器人管理者约束下的成功等级概率。
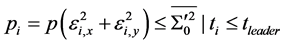(8)
3.3. 解决多机器人冲突的集成适应度函数
多机器人路径规划是要求各机器人能避开动态运行的障碍物，且机器人之间不能相碰。我们把机器人是否在安全范围内，结合机器人本身预测回报值和各机器人等级概率三方面考虑来设计解决机器人冲突的集成适应度函数。
1) 是否在安全之内
我们把所有的障碍物和机器人都视为质点，每个障碍物都有一个安全半径，若机器人与障碍物的距离大于安全半径，则认为是安全的；若小于安全半径，则认为是不安全。障碍物与机器人每一个路点
之间的距离d与安全半径R之间的关系如下：
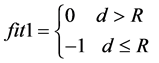(9)
其中
，障碍物坐标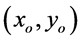
，机器人坐标为
。
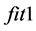的值表明只要机器人质点与障碍物的距离在安全半径之外，则其适应度值为0，若有一个路径点与障碍物的距离在安全半径之内，则适应度为−1。
2) 机器人的预测回报适应度函数
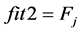(10)
3) 机器人的成功等级概率适应度函数
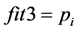(11)
综合上述因素，机器人的集成适应度函数为：
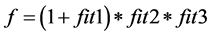(12)
3.4. 解决多机器人路径规划冲突的等级策略 [10]
本文采用离散启发式机器学习算法，结合Q学习和XCS算法共同解决多机器人路径规划中的冲突问题。LS-SVM获得的最优学习策略作为XCS的初始规则集。XCS通过与环境的交互，可以发现一组用于指导机器人避碰的学习规则，为机器人选择动作提供实时、动态的反馈，使机器人自主地学习到最优避碰规划策略。
Step 1：最小二乘支持向量机产生的最优学习策略作为XCS的初始规则集，并随机执行其中的学习策略。
Step 2：将消息列表中的消息与当前避碰规则的条件部分进行匹配，匹配的避碰规则送入匹配规则集。
Step 3：从匹配规则集中选择合适的避碰编码规则送往效应器，引导机器人产生相应的避碰动作，并依据反馈值来判断避碰效果。
Step 4：重复Step 2~Step 3过程，不断从匹配规则集中选择合适的避碰动作编码规则送往效应器，引导机器人产生相应的动作，直到匹配规则集为空或定时启动避碰规则发现机制。
Step 5：规则发现系统采用遗传算法和规则覆盖算法构造新的避碰规则。
Step 6：对产生的新的避碰规则进行规则合并，使其能概括以前的两个样本，滤除相似的个体，减少基因的单一性，加快了学习收敛速度。产生的新学习个体规则送入规则集，经过XCS发送到其公共规则集中，供其它机器人XCS产生新避碰规则时共享。
Step 7：如果机器人未达到避碰效果，则返回Step 2。
4. 仿真实验和分析
为了验证算法在多机器人的路径规划冲突中的有效性，以及提高多机器人系统解决路径规划冲突的能力的可行性。下面实验对所提算法进行全方位的验证比较，实验在不同的场景中进行。S和G分别为机器人初始和目标位置，O1~O3为动态障碍物，其它为一般静态障碍物。
实验场景一、U型障碍物的动态狭隘环境
图1为U型障碍物的形状，所有图中G表示机器人目标位置，S表示机器人初始位置。空心圆表示动态障碍物。
图2为多机器人系统在连续五个U型狭隘环境下的运动轨迹，动态障碍物(编号1~3)分别在所属的U型狭隘环境中作上下运动。尽管路途中有连续多个U型陷阱，机器人经过前期个体和团队训练阶段的强化学习，机器人均能摆脱U型陷阱的局部最优，四个机器人最终均顺利到达目标位置G点。
实验场景二、狭窄通道的多障碍物动态狭隘环境
图3为机器人在狭窄通道环境下的运动轨迹。由于图3左图中危险品为静态障碍物，机器人在此环境下能够顺利绕过危险品障碍物的运动轨迹。图3右图内有两个作水平运动的动态障碍物(编号1~2)，机器人在绕过危险品障碍物后，能够精确预测到第一个动态障碍物2的位置，且直线快速通过动态障碍物2的移动区域，然后绕过第二个动态障碍物1，从而完成机器人在狭窄通道环境下的整体运动规划，都能产生平滑的轨迹。
图4为多机器人在狭窄通道环境下的运动轨迹，动态障碍物(编号1~3)均在所属环境下作上下直线运动，所有参与规划的机器人均取得较满意的模拟曲线。在动态狭隘环境下，由于XCS具有较强预测回报能力和环境学习能力，所有机器人都能取得满意的运动轨迹和稳定的收敛效果。
实验场景三、凸凹多障碍物的动态狭隘环境
图5为凸凹多障碍物形状。图6为多机器人系统在有多个凸凹多障碍物狭隘环境下的运动轨迹。尽
Figure 1. The shape of U-shaped obstacle
图1. U型障碍物的形状
Figure 2. Multi-robot motion trajectories under U environment
图2. U型环境下的多机器人运动轨迹
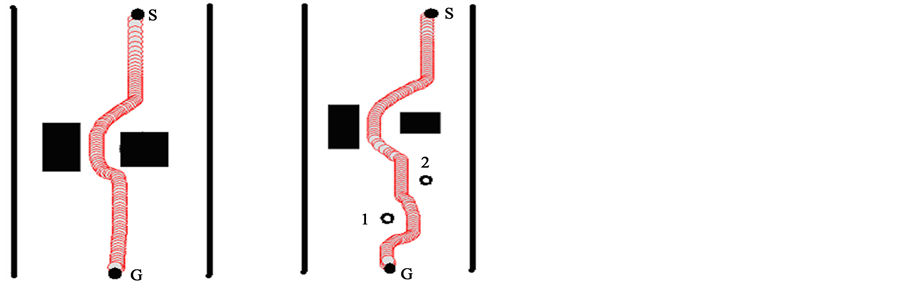
Figure 3. Robot trajectory in narrow channel environment
图3. 狭窄通道环境下的机器人运动轨迹
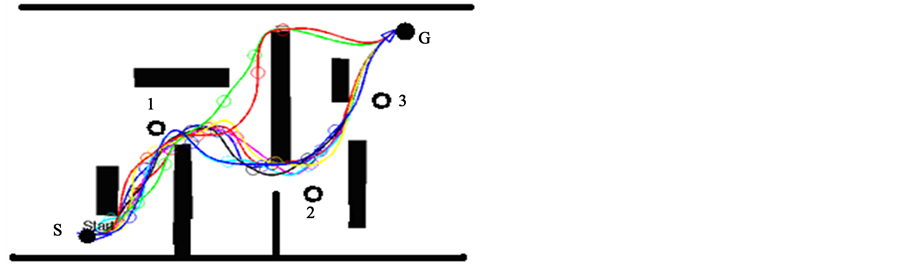
Figure 4. Multi-robot trajectories in narrow channel environment
图4. 狭窄通道环境下的多机器人运动轨迹
Figure 5. The shapes of many convex-concave obstacles
图5. 凸凹多障碍物形状
Figure 6. Multi-robot trajectories in convex-concave obstacles environment
图6. 凸凹多障碍物环境下多机器人运动轨迹
管有多个易于陷入局部最小的风险陷阱，但机器人(R1、R2、R3)在文献[10] 所述的行为控制方法follow_wall、avoid_obstacle、move_to_goal的引导下，结合本文提出的XCS集成算法，机器人R1、R2和R3均顺利躲避附近移动的动态障碍物，所有机器人能够非常稳定的到达各自的目标。在安全性方面，图6最危险的地带在凸凹障碍物周围，在30次试验中机器人R1、R2和R3分别成功29、29和30次，整个多机器人系统路径规划成功率在95%以上，表现出良好的动态避障性能。
5. 结束语
本文提出采用基于XCS的离散启发式方法用于单个机器人的路径规划，机器人的优先权由其XCS的预测回报值来确定，而由集中式高水平的规划机器人动态分配各机器人的优先顺序，以解决多机器人间的冲突，共同完成多机器人系统的路径规划。很大程度上解决了遗传算法的早熟收敛、局部最优解、占据存储空间较大、收敛数度慢等问题，提高了多机器人发现安全路径的能力。
基金项目
2013河南省高等学校“专业综合改革试点”项目；河南省教育厅重点基金资助项目(12B520047)。