1. 引言
随着我国航天事业的飞速发展，测量船承担的试验任务对测控天线测角精度的要求也越来越高 [1] - [3] 。轴角编码精度的提高也成为提高测角精度的一个重要途径，而作为测角精度基础的轴角编码精度的检定却发现存在满足不了指标要求的情况 [2] - [5] 。
当前测量船使用的测控雷达均为两轴式天线，所涉及到轴角编码精度检测有方位和俯仰。对于方位轴角编码检测原理：与高精度经纬仪比对，检测方位轴角编码器精度。高精度经纬仪与测量设备同时测量同一固定目标，对测量数据进行比对作差，统计方位轴角编码器的精度。对于俯仰轴角编码检测方法原理：与高精度角摆仪比对，检测俯仰轴角编码器精度，对测量数据进行比对作差，统计俯仰轴角编码器的精度。
从检测过程中，发现以下问题：方位每转动15˚读取一次数据，俯仰每转动10˚读取一次数据，每次检测的角度间隔太宽，不能反映出编码器编码真实误差情况；由于测量俯仰轴角编码器精度的角摆仪只能按照设定的程序进行检测和记录，不在其记录范围内的数据均不能记录和计算，而条件中又要俯仰抱闸后检测，在重力和风力的影响下这个条件很难满足，若在加电消隙的情况下检测，天线俯仰始终在用力，角摆仪不能读取稳定的数据；即使检测出精度不满足指标要求，现场也不能及时得到解决，更不能将误差进行补偿，只能重复检测希望下次检测能满足指标要求。
针对轴角编码精度检测过程中发现的问题及满足不了指标要求的情况，本文在分析影响当前测量船轴角编码误差产生的主要因素(双通道多极旋转变压器的误差、Resolver-to-Digital Converter (RDC)转化误差、量化误差)的基础上，进行了轴角编码精度检测方法的研究，并提出了使用误差补偿方法和新的检测方法。
2. 轴角编码器误差分析
测量船测控天线测角系统组成如图1所示。角度敏感元件采用的是双通道多极旋转变压器。此类旋转变压器本身设计上就存在原理性误差，同时也存在结构安装上的工艺误差和旋转变压器运行的环境而影响导致的误差。现有轴角编码器使用的模数信号转换芯片(RDC)，其转换过程中存在电路误差。最后是数码量化误差。
2.1. 双通道多极旋转变压器原理误差
2.1.1. 双通道多极旋转变压器工作原理
双通道多极旋转变压器由两个通道组合而成。一般为共磁路结构组成，其一为粗通道，另一称为精
通道。而转子为激磁，定子为输出。当转子在不同的角度时，定子所切割的磁场强度不同，故感应在定子上的电压就不同。当转子转动角度为θ时，粗精绕组上分别输电压，它们之间成正、余弦关系，工作原理见图2 [1] 。设激磁电压为 [6] - [8] ：
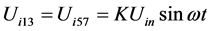(1)
则粗通道正、余弦绕组上输出电压为 [6] ：
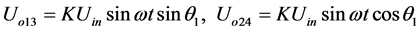(2)
则精通道正、余弦绕组上输出电压为 [6] ：
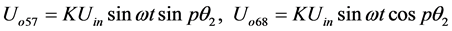(3)
式中，θ为转子转动的角度，θ1为粗测的角度，θ2为精测的角度；K为双通道多极旋转变压器定子与转子绕组间的比例系数，与其线圈匝数比相关；p为多极旋转变压器的极数。
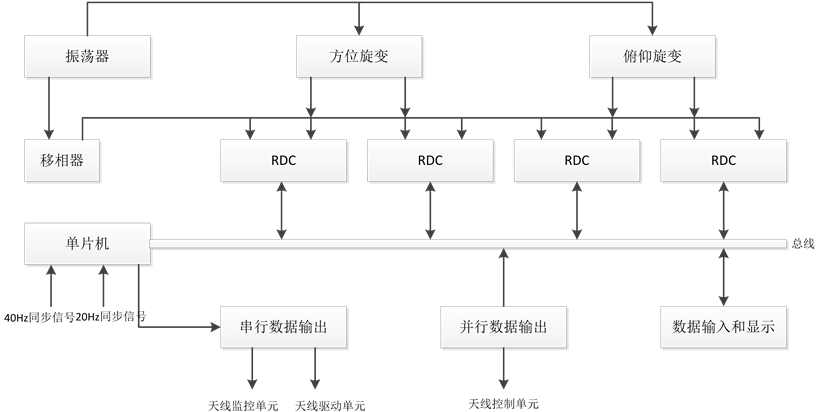
Figure 1. Structure of antenna’s angle measurement system
图1. 天线测角系统硬件组成框图
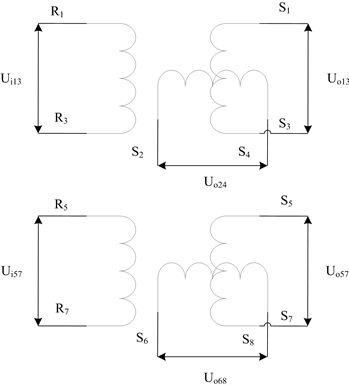
Figure 2. Operational principle of twin-channel multi-pole resolvers
图2. 双通道多极性旋转变压器工作原理
2.1.2. 双通道多极旋转变压器误差分析
由于生产出的双通道多极旋转变压器的定、转子气隙不均匀、激磁电源波形失真、输入、输出信号相移会引起的误差，这一类误差称为电气误差 [1] - [3] 。
1) 双通道多极旋转变压器电气误差分析
双通道多极旋转变压器的电气误差存在以下三种主要误差：
由于输出两相R1R3正弦与R2R4余弦绕组电压的变压比之间的存在一定的不对称度会引起变压比均衡性误差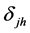
。不对称度可表为：
。这时的正余弦绕组输出电压为 [2] [4] [6] ：
(4)
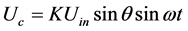(5)
此时，输出的电压对应的角度输出为 [2] ：
(6)
而理想状态下应为 [2] ：
(7)
由于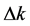
很小的原因，此时变压比均衡性误差
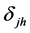为 [2] ：
(8)
交轴误差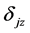
为输出两相正弦与余弦绕组非正交引起的误差，假设余弦绕组偏离正交的正弦绕组
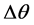角度值，则此时输出电压为 [2] ：
(9)
(10)
由于
很小的原因，一般来说是分(min)级别的，此时的交轴误差表达式为 [2] ：
(11)
函数误差
为输出两相正弦与余弦绕组本身引起的误差，此时正、余弦绕组输出电压为 [2] ：
(12)
(13)
其中：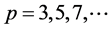
；
；
，
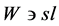为原、付方基波有效匝；
，
为原、付方谐波有效匝。
由于函数误差很小的原因，也是分(min)级别的，其表达式为 [2] ：
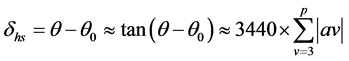(14)
2.2. 旋转变压器数字转换器转化误差
旋转变压器数字转换器转化误差指的是RDC芯片的转化误差，对于轴角编码器而言，每一路粗或精通道均有一片RDC芯片进行实时的转化，此芯片在处理旋转变压器的信号时电路上会产生一些误差。工作原理如图3所示。一般说来主要存在以下两种误差 [8] [9] ：
若数字转换器发生的正余弦信号非正交，将会导致轴角数字转换器的转换误差
。假设余弦函数发生器产生的信号偏离正交位置
，可以推导出所导致的误差为 [2] ：
(15)
由于函数发生器中的MDAC (乘法数模转换器)的放大倍数不等，自旋转变压器输入的信号的衰减和放大倍数不等时均会使两相幅值发生偏差称为变压比均衡性误差
。假设余弦函数发生器的电压幅值比正弦函数发生器的电压幅值大m倍，推导可得 [2] ：
(16)
假定正弦函数发生器发生电压幅值比余弦函数发生器所产生的电压幅值大m倍时可得 [2] ：
(17)
2.3. 数码的量化误差
数码的量化误差取决于数码的位数。在单片机的软件中经过粗码和精码组合，假设粗码取6位、精码取14位组合成20位二进制码，它能够表示的角度范围为360˚电气角，精度理论上最高能达到1.236″。
2.4. 误差综合分析
以上的误差原理分析可以整理为表1。
从表1可以发现：旋转变压器的交轴误差、变压器均衡性误差与RDC的交轴误差、变压比误差表达式相似。实验统计表明，这几项误差占了整个电气误差的85%。同时，电气误差又是轴角编码器的主要误差。
3. 新的检测方法的提出及误差补偿
3.1. 新的检测方法的提出
在测控天线中，轴角编码器所给出的方位角度和俯仰角度即认为天线的机械轴角度，它的精度直接影响到天线的测角精度。由于以上误差的原因，当前的检测方法又不能真实地检测出轴角编码器的精度和误差情况，所以提出利用新的检测工具进行轴角编码器精度的检测。
3.1.1. 激光跟踪仪
当前使用的高精度光学经纬仪不能连续记录数据而且本身测量精度也不高，反映不出误差波形规律。我们可以采用精度较高的激光跟踪仪，它不仅精度高，实时快速、而且能够动态测量。激光跟踪仪的本质是一种球坐标测量系统，其基本原理是测量目标点的距离及水平和垂直方向的偏转角，建立以测站为中心的极坐标系。距离分量由激光干涉仪测量，角度分量由高精度角度编码器测量。在同一时统下，利
用激光跟踪仪实时地测量当前天线的方位或俯仰角度值，然后与同时刻的轴角编码器记录下来的角度数据比对，完成对轴角编码精度的检测。
3.1.2. 激光陀螺
我们不仅可以采用精度较高的激光跟踪仪，还可以使用激光陀螺进行轴角编码器精度的检定。激光陀螺同样可以实时快速、而且能够动态敏感出角度的变化。由于激光陀螺精度更高，它也可以实时地测量当前天线的方位或俯仰角度值。我们可以采取与激光经纬仪同样的方法来完成对轴角编码精度的检测。
3.2. 误差的补偿
检测出轴角编码精度不是最终目的，最终我们要通过采用合理的方法提高编码精度以满足指标要求 [9] 。对于主要的差源：旋转变压器和RDC芯片自身电气方面的造成的误差，在软件中利用Back Propagation (BP)神经网络学习算法来进行补偿，做到减小误差的目的。
3.2.1. 误差补偿方案
BP神经网络自我学习的能力使其具有以任意精度逼近任意非线性连续函数的特点，并适合数据点较
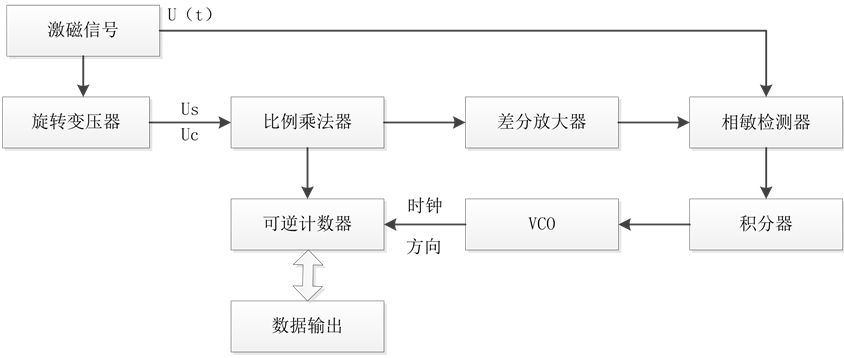
Figure 3. Operation principle of RDC
图3. 跟踪反馈型轴角编码工作原理框图
Table 1. System resulting data of standard experiment
表1. 基于双通道多极旋转变压器的轴角编码误差数学表达式
多的场合。对于旋转变压器的非线性误差可进行较好的补偿。在单片机软件中，BP神经网络学习算法采用具有教师训练模式，首先把网络的实际输出和希望输出进行比较，然后根据两者之间的差值调整网络的权值，在经过反复调整后，最终使误差减少。BP神经网络学习算法程序流程图如图4所示。
由于轴角编码器角度误差曲线呈现一定的规律性，采用神经网络模型进行逼近，而且采集的数据点较多，以轴角编码器的角度值作为输入变量，以激光陀螺测得同时刻的角度值作为目标输出值，为单输入单输出网络，选用3层的BP神经网络，隐含层设为20个节点，激励函数选用tansig [5] [9] 。进行训练后，得到的激励函数训练权值和阈值再由单片机实时进行误差的补偿。其补偿前后的角度误差曲线如图5所示。实验证明最终补偿后角度误差能从最高23″减小到5″以内。
4. 结束语
本文从测量船测控天线轴角编码精度的检测方法入手，指出了现有轴角编码检测精度方法的局限性。深入分析现有轴角编码器的误差来源及其规律，并提出了采用新的检测工具来检测编码精度及对应的方
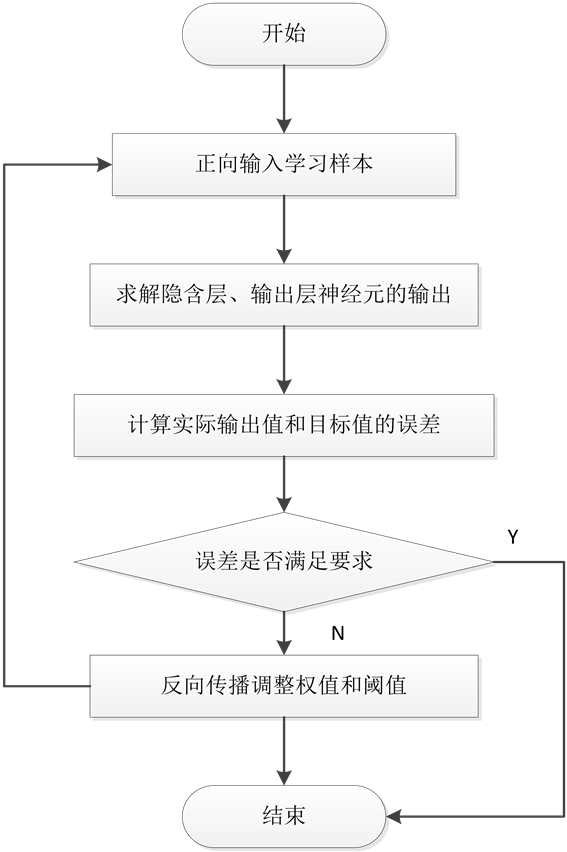
Figure 4. Flow chart of learning algorithm of BP ANN
图4. BP神经网络学习算法程序流程图
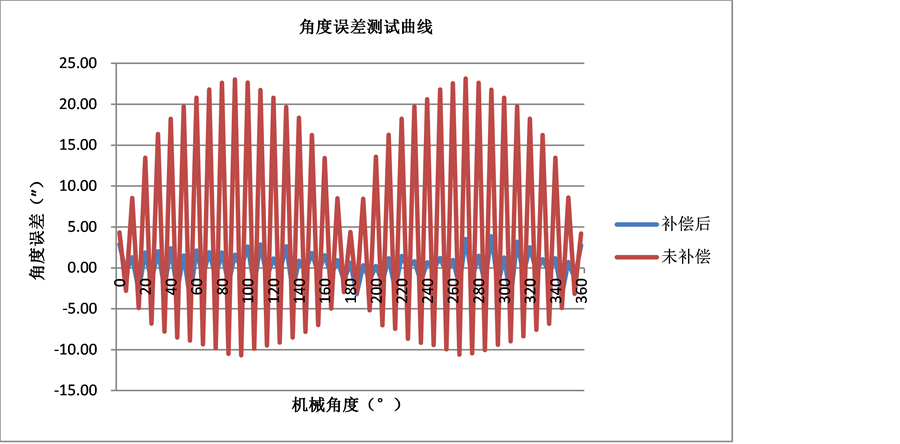
Figure 5. Comparison of before and after error compensation
图5. 未补偿和补偿后的角度对比
法。最后，提出了对现有的轴角编码器中实现误差补偿的方法及在应用中获得了良好效果。