1. 引言
在数控加工中,经常遇到如飞机的的机翼、汽车流线型覆盖件成形模具型腔、汽轮机叶片等许多复杂外形型面的零件。面对这类曲线曲面的描述通常采用的方法是 方法,它既能表示自由曲线曲面,又能表示一些规则的二次曲线曲面。但NURBS曲线的参数表达式比较复杂,插补运算量大,且由型值点逆求控制点的反求运算较难实现,不易于实现直接插补。为此,本课题组在文献[1] 中提出了一种新型样条曲线——可调形三次三角插值样条曲线,这种样条曲线的插值样条表达式中含有三角函数多项式,通过选择合适的控制点和形状可调参数,该插值样条可以精确表示直线、圆弧、椭圆以及自由曲线等常见工程曲线。由于该使用的三次三角插值样条避免了使用有理的数学表达形式,故其表达式比较简洁,所需的计算量也相对较小,并且能够实现实时插补,这很好的为插值曲线及曲面的设计,提供了一种全新的理论方法。
方法,它既能表示自由曲线曲面,又能表示一些规则的二次曲线曲面。但NURBS曲线的参数表达式比较复杂,插补运算量大,且由型值点逆求控制点的反求运算较难实现,不易于实现直接插补。为此,本课题组在文献[1] 中提出了一种新型样条曲线——可调形三次三角插值样条曲线,这种样条曲线的插值样条表达式中含有三角函数多项式,通过选择合适的控制点和形状可调参数,该插值样条可以精确表示直线、圆弧、椭圆以及自由曲线等常见工程曲线。由于该使用的三次三角插值样条避免了使用有理的数学表达形式,故其表达式比较简洁,所需的计算量也相对较小,并且能够实现实时插补,这很好的为插值曲线及曲面的设计,提供了一种全新的理论方法。
本文针对该三次三角样条曲线提出了一种新的插补计算方法,该法有效地提高了加工精度和加工过程的可靠性。其插补思想是:使用若干顺序连接的微小直线段逼近用户程序给定的插值样条曲线轮廓。将直线段映射到参变量空间,得到参变量的增量值,再通过控制参变量u,求取对应的轨迹空间中的映射点,最终得到插补点的坐标值。以此不断重复直到插补终点,可得到整个离散化插补轨迹。
2. 三次三角插值样条曲线
定义 对任意给定实数k ≥ 0,参变量u: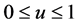 ,称以下一组关于u的函数为带形状可调参数
,称以下一组关于u的函数为带形状可调参数 的三次三角Cardinal样条基函数。
的三次三角Cardinal样条基函数。
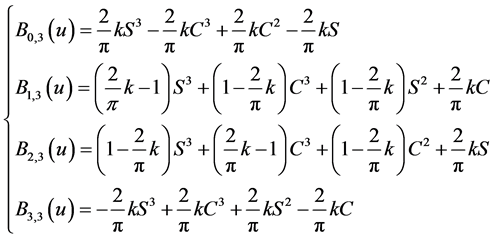 (1)
(1)
其中 ,
, 。
。
设qt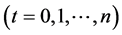 为R2或R3中给定的一组控制点(n ≥ 3),定义参数曲线段
为R2或R3中给定的一组控制点(n ≥ 3),定义参数曲线段
 (2)
(2)
( ,i为曲线段号,
,i为曲线段号, ),为由每四个顺序控制点qi-1,qi,qi+1,qi+2所构造的分段三次三角样条曲线,所有曲线段Pi(u)有序组成的曲线P(u)称为三次三角样条曲线。
),为由每四个顺序控制点qi-1,qi,qi+1,qi+2所构造的分段三次三角样条曲线,所有曲线段Pi(u)有序组成的曲线P(u)称为三次三角样条曲线。
3. 三次三角插值样条曲线的插补计算方法
数据采样插补实质上是使用一系列首尾相连的微小直线段来逼近给定曲线。由于这些线段是按加工时间分割的,因此数据采样插补又称为时间分割法插补,近代数控系统轨迹插补在数据采样原理的基础上产生了很多新的插补算法。本文就数据采样插补原理产生的三次三角插值样条曲线的插补算法进行研究。
3.1. 三次三角插值样条曲线的插补原理
根据三次三角插值样条曲线的定义知,该曲线为多项式形式,可插值于所有给定的控制点,且整体达到C1连续,可以精确表示工程中一些常见的曲线,其具有计算简单、构造灵活、高精度等特点。下面讨论其插补原理:
由样条曲线原理可知,这类曲线为分段参数曲线,当参变量 在其取值期间上连续变化时,曲线上终点的位置矢量P(u)可公式(2)求出。
公式(2)的简化表达式为:
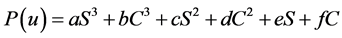 (3)
(3)
式中:a,b,c, d,e,f为常数矢量, ,
, ,
,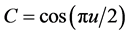
各项系数将随插值点位置的变化而变化,即取不同的值,故三次三角插值样条曲线是一个变系数三次参数曲线插补问题。
3.2. 三次三角插值样条曲线插补实现原理和步骤
三次三角样条曲线的插补过程的直接控制量是参变量u,而最终的被控量是插补点的坐标值以及插补点所沿插补轨迹的进给速度,先利用轨迹空间到参变量空间的映射和参变量,然后再通过参变量空间到轨迹空间的映射这两大步骤的相互转换来完成。具体步骤如下:1) 根据三次三角插值样条曲线现有的几何信息,确定轨迹计算公式中的相关系数。2) 按照用户程序的进给速度、加减速要求以及允许误差,在插补周期中产生空间小直线段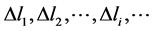 去逼近被插补曲线,逐步求得各插补直线端点
去逼近被插补曲线,逐步求得各插补直线端点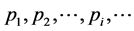 的坐标值。3) 将直线映射到参变量空间,得到与其对应的参变量空间中的微小直线段即参变量的增量值,求取与参变量空间中下一点插补点的坐标。
的坐标值。3) 将直线映射到参变量空间,得到与其对应的参变量空间中的微小直线段即参变量的增量值,求取与参变量空间中下一点插补点的坐标。
4. 三次三角插值样条曲线的插补的实现方法
4.1. 插补预处理
为了减少三次三插值样条曲线在插补中的计算量,可将插补算法中一些可以一次性计算的任务放在实时插补前的预处理阶段完成。这些任务主要包括轨迹表达系数的求取和导数表达式系数的求取 [2] 。
轨迹表达式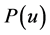 系数的求取是根据CAD/CAM给出的样条曲线描述信息,在实时插补前一次性求解出轨迹计算公式所有系数a,b,c,d,e,f,对于三次三角插值样条曲线,如CAD/CAM给出的原始信息为控制点序列
系数的求取是根据CAD/CAM给出的样条曲线描述信息,在实时插补前一次性求解出轨迹计算公式所有系数a,b,c,d,e,f,对于三次三角插值样条曲线,如CAD/CAM给出的原始信息为控制点序列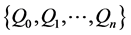 ,则曲线表达式为:
,则曲线表达式为:
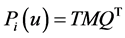 (4)
(4)
式中: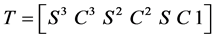 ;M为常数矩阵;
;M为常数矩阵;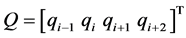 ;i为曲线段号。
;i为曲线段号。
三次三角插值样条曲线的常数矩阵M为:

代入(4)式得:
 (5)
(5)
比较式(3)和(5)可得轨迹计算公式(3)的系数与控制点序列的关系为:
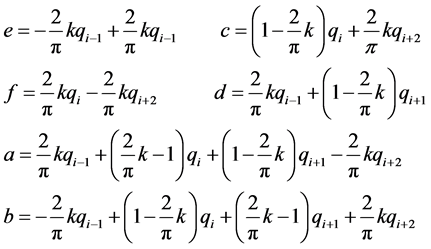 (6)
(6)
在样条插补过程中需要计算曲线弧长对参变量的变化率之值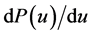 ,为了减少实时计算的工作量,表达式中的导数表达式系数也在预处理阶段求出。设三次三角插值样条曲线表达式为:
,为了减少实时计算的工作量,表达式中的导数表达式系数也在预处理阶段求出。设三次三角插值样条曲线表达式为:
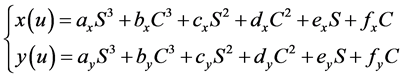 (7)
(7)
式中:参数 ,
,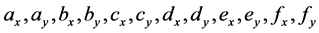 为常系数。
为常系数。
在分析自由曲面时,实时计算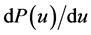 的值为:
的值为:
 (8)
(8)
其中:
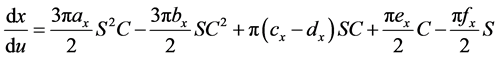
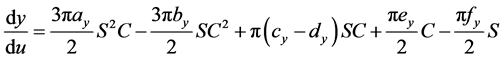
代入得:
 (9)
(9)
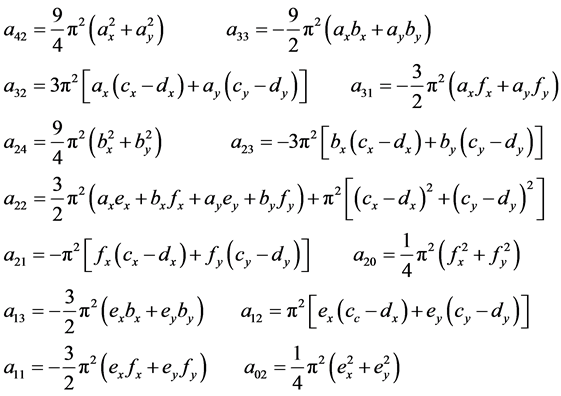 (10)
(10)
多项式的系数的数值每一段曲线上的值分别是定值,因此可以在插补预处理阶段通过一次性计算预先求出,以便简化后续计算。
4.2. 三次三角插值样条曲线实时插补计算
因为数控系统的插补过程实质是每个微小直线段的两端点坐标的过程,这些点都在参数曲线上,而参数曲线上的点又是与参数值一一对应的,所以参数曲线的插补过程可以转化成连续求解一系列参数值的问题,以此计算插补轨迹上的下一点Pi+1的坐标值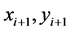 。为了使刀具在曲线插补过程中能够平滑运动,保证其加工产品的质量和精度,论文不采用等参数分割插补算法。而是采用以瞬时进给速度为控制目标,允许误差为约束条件的实时插补算法 [3] - [7] 。实现过程如下:
。为了使刀具在曲线插补过程中能够平滑运动,保证其加工产品的质量和精度,论文不采用等参数分割插补算法。而是采用以瞬时进给速度为控制目标,允许误差为约束条件的实时插补算法 [3] - [7] 。实现过程如下:
假设给定的瞬时进给速度 ,
,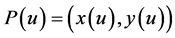 为所要插补的空间参数曲线,根据微分几何可知
为所要插补的空间参数曲线,根据微分几何可知
 (11)
(11)
式中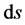 是曲线的微分弧长,
是曲线的微分弧长, 是时间微分,
是时间微分,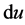 是参数
是参数 的微分。
的微分。
设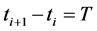 为数控系统的插补周期ms;u是关于时间t的函数,有:
为数控系统的插补周期ms;u是关于时间t的函数,有:
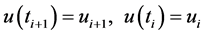
对上式进行微分得
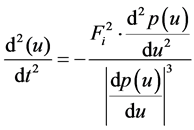 (12)
(12)
利用泰勒级数得展开式
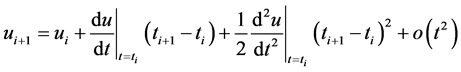 (13)
(13)
由插补递推公式的一阶近似得:
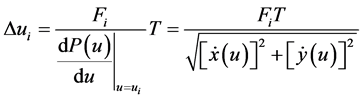 (14)
(14)
二阶近似得:
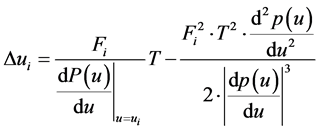 (15)
(15)
由于现在数控系统的插补周期T一般都很小,在曲率半径不太小的情况取一阶近似迭代求得的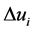 ,如果曲线曲率半径很小,便采用二阶近似下求得的
,如果曲线曲率半径很小,便采用二阶近似下求得的 。
。
通过以上过程求出当前周期的 的值后,便可进一步计算下一插补周期参变量
的值后,便可进一步计算下一插补周期参变量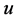 的取值
的取值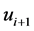 为:
为:
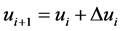 (16)
(16)
然后,根据求得的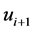 和轨迹计算公式,即可求出样条曲线的下一插补
和轨迹计算公式,即可求出样条曲线的下一插补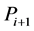 点的坐标增量值
点的坐标增量值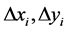 ,从而可以求得下一插补点
,从而可以求得下一插补点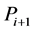 的坐标值
的坐标值 。
。
计算 和
和 ,即:
,即:
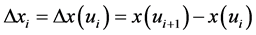
同理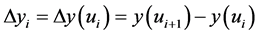
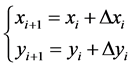 (17)
(17)
再令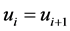 ,不断重复以上过程直至到达样条曲线终点就可以求出所有插补点,这样可得到整个离散化的插补轨迹。
,不断重复以上过程直至到达样条曲线终点就可以求出所有插补点,这样可得到整个离散化的插补轨迹。
5. 误差控制
我们知道数控系统实时插补是采用泰勒展开式计算各插补周期的参变量增量,然后由该参数值映射到轨迹空间实现轨迹插补不停向前进行,因此插补过程中并没有累积误差,但在一个插补周期内,插补轨迹使用小线段去逼近三次三角样条曲线,这样就会存在轮廓误差,近似地可以认为是弦高误差 [8] 。插补误差图如图1所示。
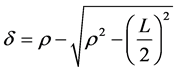 (18)
(18)
式中: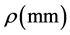 为前一插补点的曲率半径,其值等于该点曲率的倒数,
为前一插补点的曲率半径,其值等于该点曲率的倒数,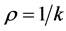 ;
;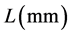 近似看作一个插补周期的插补长度,有
近似看作一个插补周期的插补长度,有 。
。
其中局部的曲率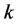 由如下公式所得:
由如下公式所得:
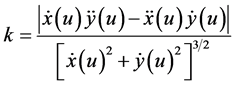
当最大允许轮廓误差为 时,则瞬时进给速度
时,则瞬时进给速度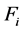 需要满足如下条件:
需要满足如下条件:
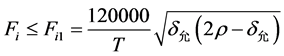 (19)
(19)
当采用高速切削加工曲线曲面时,由于曲率的存在,必然会引起较大的进给加速度。若加速度过大,超过机床进给系统动态刚度的设计承受能力,就会给整个加工系统、加工过程和零件的加工质量造成严重影响。因此,必须将加工进给的加速度限制在允许的范围内。当最大允许法向加速度为 时,进给速度
时,进给速度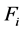 需要满足如下条件:
需要满足如下条件:
 (20)
(20)
为避免式中曲率半径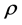 的计算不便,比较式(19)和(20),有:
的计算不便,比较式(19)和(20),有:
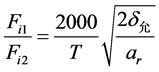 (21)
(21)
因此实际的瞬时进给速度的取值为:

Figure 1. Xiaohegou hydrological station of the water system map
图1. 插补误差示意图
式中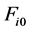 为给定的瞬时进给速度,
为给定的瞬时进给速度, 为满足最大允许误差
为满足最大允许误差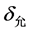 的进给速度,
的进给速度, 为满足最大法向加速度的进给速度。该瞬时进给速度同时满足了给定进给速度、最大允许误差及最大法向加速度等约束条件,从而很好地满足了现代数控加工对于高速高精度的要求。
为满足最大法向加速度的进给速度。该瞬时进给速度同时满足了给定进给速度、最大允许误差及最大法向加速度等约束条件,从而很好地满足了现代数控加工对于高速高精度的要求。
例如,现采用高速加工一段三次三角插值样条曲线,其最小曲率半径为 ,指令进给速度为21 m/min,要求零件的轮廓误差小于
,指令进给速度为21 m/min,要求零件的轮廓误差小于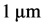 ,机床的进给加速度小于0.2g (g为重力加速度)。现在利用本文提出的插补算法控制,设插补周期为1 ms。计算可得
,机床的进给加速度小于0.2g (g为重力加速度)。现在利用本文提出的插补算法控制,设插补周期为1 ms。计算可得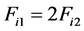 ,即进给加速度较轮廓精度要求得到的进给速度长更小。当加工处于曲率较小的区域时,可以正常进给速度21 m/min加工,对应的插补进给步长为L = 0.35 mm。由式(20)可知,当曲率半径小于62.5 mm时,
,即进给加速度较轮廓精度要求得到的进给速度长更小。当加工处于曲率较小的区域时,可以正常进给速度21 m/min加工,对应的插补进给步长为L = 0.35 mm。由式(20)可知,当曲率半径小于62.5 mm时, 插补进给速度由
插补进给速度由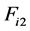 决定随着曲率的增大而逐渐下降,步长随之减少,至最小曲率半径50 mm处,进给速度降至最低,
决定随着曲率的增大而逐渐下降,步长随之减少,至最小曲率半径50 mm处,进给速度降至最低,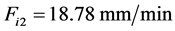 ,对应的步长为L = 0.313 mm,轮廓误差为
,对应的步长为L = 0.313 mm,轮廓误差为 。由此可见,该插补算法可以满足曲线高速高精度加工的各项要求。
。由此可见,该插补算法可以满足曲线高速高精度加工的各项要求。
6. 结束语
1) 本文提出了一种自由曲线的简洁表达式,实现了对常见数控加工刀具运动轨迹曲线的统一精确数学表示和自由曲线的快速插补;
2) 基于数据采样插补原理,实现了三次三角插值样条曲线的实时插补计算;
3) 该算法插补弦长的波动较小,具有良好的速度稳定性从而提高加工精度。