1. 引言
混沌是动力系统的一种复杂表现,已经在水文、医学、经济等众多领域中发现混沌现象 [1] - [4] 。对混沌时间序列的建模和预测已经成为研究具有混沌现象的各类时间序列的热点 [5] - [7] 。应用混沌理论结合其他方法对其进行预测,其效果更好,如水文预测 [8] 、风电池功率预测 [9] 、交通流预测 [10] - [13] 等。
混沌时间序列预测的早期方法可归纳为 [7] :全局法,最大Lyapunov指数法,局域法以及自适应预测法。现今方法则可总结为:人工神经网络模型 [14] - [19] ,支持向量机(Support Vector Machine,简记为SVM)模型 [20] - [26] ,复合模型 [9] [27] 和改进的自适应预测模型 [13] 。但这些模型和方法较为复杂,实现繁琐,且有过拟合、局部极小和易受主观经验的影响等问题。线性模型已经有几十年的应用历史。由线性模型构建的针对混沌时间序列的局域线性模型十分简单可行,文献 [8] 和 [28] 对局域线性预测模型又进行了改进,提出了两种新的局域预测方法NLLP1 [28] 和NLLP2 [8] ,使得局域线性预测模型的预测精度和预测长度有了很大提升。然而,局域线性模型的线性化过程掩盖了混沌时间序列的非线性特性,限制了局域线性模型的适用范围。
为了克服这些方法的缺点,本文依据混沌时间序列的局部特性和非线性特性,结合相空间重构的思想和多项式系数模型(Polynomial Coefficient Model) [29] 提出局域多项式系数自回归混沌时间序列预测模型(Local Polynomial-coefficient Prediction,简记为LPP),并根据时域和状态域定阶给出了两种不同的LPP方法。LPP是一种局域非线性方法,可将其看成对局域线性法的改进。LPP模型可以很好的描述混沌时序的非线性特性,能够在不增加较大计算量的前提下提高预测精度,同神经网络模型和SVM模型相比,结构简洁且易于实现。通过对三种典型混沌时间序列(Logistic映射、Henon映射和Lorenz系统)的仿真实验表明,本文方法是有效的。
2. LPP预测模型
2.1. 混沌时间序列的相空间重构
利用Takens嵌入定理 [30] 即可重构混沌时间序列,提升预测效果。设单变量混沌时间序列为 ,进行相空间重构可得,
,进行相空间重构可得,
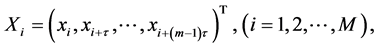 (1)
(1)
式中, 为嵌入维数,
为嵌入维数,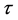 为延迟时间,
为延迟时间, 是重构相空间中相点的个数,这
是重构相空间中相点的个数,这 个相点的连线构成了
个相点的连线构成了 维相空间中的轨线。对重构后的相空间,存在光滑映射
维相空间中的轨线。对重构后的相空间,存在光滑映射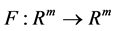 ,即
,即
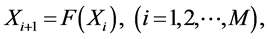 (2)
(2)
从 分离出
分离出 ,即有
,即有
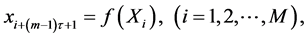 (3)
(3)
如果能够求出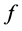 或找到
或找到 的一个逼近模型
的一个逼近模型 ,就能对未来值进行预测。
,就能对未来值进行预测。
2.2. LPP模型
局域线性模型(简称LPP模型)是一个局域线性回归模型,混沌时间序列的嵌入维数 和延迟时间
和延迟时间 可根据文献 [31] 确定,有如下形式
可根据文献 [31] 确定,有如下形式
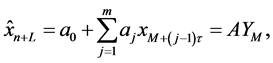 (4)
(4)
式中, 为系数矩阵,
为系数矩阵, ,
,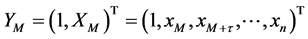 ,
, 是预测步长。
是预测步长。
这里,将重构相空间的嵌入维数看成预测阶数。为了估计 ,要从相空间中找到当前状态(以相点
,要从相空间中找到当前状态(以相点 为例)的
为例)的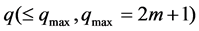 个邻近点 [8] ,邻近点的选取通过欧式距离
个邻近点 [8] ,邻近点的选取通过欧式距离
 来确定。距离越近,当前状态
来确定。距离越近,当前状态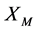 与其他点状态演化相似程度越大,模型的预测精度越高。将
与其他点状态演化相似程度越大,模型的预测精度越高。将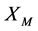 的
的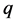 个邻近点
个邻近点 代入(4)式中,可求得
代入(4)式中,可求得 的一个最小二乘估计
的一个最小二乘估计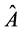 ,将
,将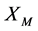 代入(4)式中,可求得
代入(4)式中,可求得 的一个估计
的一个估计 ,每次所得新值都加入训练数据集中,然后进行下一步预测,即将
,每次所得新值都加入训练数据集中,然后进行下一步预测,即将 看作
看作 ,则可求得
,则可求得 。
。
将线性模型的系数改为Taylor级数展开
 (5)
(5)
式中,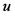 为由
为由 指定的模型依赖变量
指定的模型依赖变量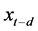 。将(5)式代入(4)式得
。将(5)式代入(4)式得
 (6)
(6)
式中,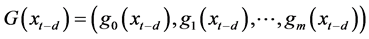 为系数矩阵,
为系数矩阵, ,
, 为数据重构后相空间的嵌入维数,
为数据重构后相空间的嵌入维数, 为延迟时间。(6)式是一种非线性模型,是局域线性模型的一个改进,利用重构相空间的局域相点对(6)式的参数进行估计,就得到了LPP模型。
为延迟时间。(6)式是一种非线性模型,是局域线性模型的一个改进,利用重构相空间的局域相点对(6)式的参数进行估计,就得到了LPP模型。
2.3. LPP模型参数的估计
为了使LPP模型有效的逼近 ,采用最小二乘估计方法,使得到的LPP模型是误差平方和最小意义下
,采用最小二乘估计方法,使得到的LPP模型是误差平方和最小意义下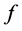 的一个逼近。将(5)代入(6)中,可得LPP模型的求和形式
的一个逼近。将(5)代入(6)中,可得LPP模型的求和形式
 (7)
(7)
设有 的
的 个邻近点为
个邻近点为 ,若记
,若记
 (8)
(8)
则(7)式有如下矩阵表达式
 (9)
(9)
式中,运算
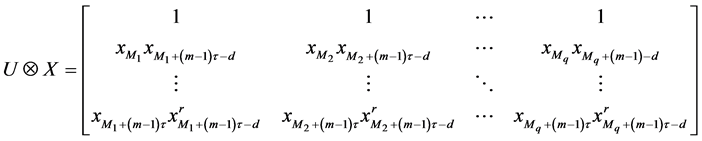
表示矩阵的kronecker积。进而根据最小二乘原理可求得 表达式为
表达式为
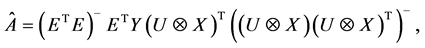 (10)
(10)
式中, 表示对
表示对 求广义逆,当
求广义逆,当 可逆时,有
可逆时,有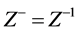 。
。
2.4. LPP模型阶次的选择
一般的,LPP模型的阶次可通过比较不同 、
、 值时模型的性能来确定,同时,模型的阶数
值时模型的性能来确定,同时,模型的阶数 也不一定要取
也不一定要取 ,因为最优嵌入维数不一定是模型的最优阶数 [28] ,这在嵌入维数较大时尤其需要注意。由于没有对模型误差进行正态假定,传统的AIC准则和BIC准则不再适用。有鉴于此,使用如下两种方案确定模型的阶次:
,因为最优嵌入维数不一定是模型的最优阶数 [28] ,这在嵌入维数较大时尤其需要注意。由于没有对模型误差进行正态假定,传统的AIC准则和BIC准则不再适用。有鉴于此,使用如下两种方案确定模型的阶次:
方案1:取使得一步预测误差平方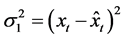 最小的
最小的 、
、 和
和 作为估计点
作为估计点 的LPP模型的阶数;
的LPP模型的阶数;
方案2:利用文献 [8] 提供的做法。定义
 (11)
(11)
式中, 为邻近点个数,
为邻近点个数,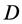 为广义自由度,定义为
为广义自由度,定义为 ,
, ,
,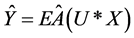 。选取使得
。选取使得 或
或 最小的
最小的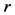 、
、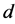 和
和 作为模型的阶次。
作为模型的阶次。
第一种方案是利用重构后混沌时间序列的时域特性进行定阶,第二种方案是利用混沌时间序列的状态域特性定阶。若使用第一种方案定阶,将此时的LPP模型记为LPP1模型,若使用第二种方案定阶,将此时的LPP模型记为LPP2模型。
基于以上分析,现给出LPP预测模型的建模步骤。
步骤1:使用相空间重构理论对实验数据进行相空间重构,求得嵌入维数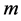 和延迟时间
和延迟时间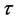 ;
;
步骤2:利用(10)式来估计系数矩阵 ,对不同的阶次
,对不同的阶次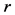 、
、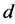 、
、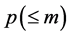 和邻域点个数
和邻域点个数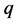 计算
计算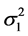 和
和 ,为了控制模型复杂度,减少计算量,限制
,为了控制模型复杂度,减少计算量,限制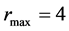 ;
;
步骤3:选取使得 或
或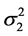 最小的
最小的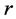 、
、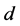 、
、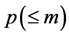 和邻域点个数
和邻域点个数 作为模型的阶次,对混沌时间序列进行一步预测;
作为模型的阶次,对混沌时间序列进行一步预测;
步骤4:将一步预测结果加入训练数据集中,重复步骤2和步骤3,进行下一步预测。
LPP模型的算法流程图如图1所示。
3. 仿真结果及讨论
下面就LPP1和LPP2预测方法同改进的局域线性模型NLLP1、NLLP2和传统局域线性模型TLLP对三种典型的非线性系统(Logistic映射、Henon映射和Lorenz系统)产生的混沌时间序列的多步预测性能进行仿真研究。以平均绝对误差MAE来评价模型预测值与真值的偏离程度,以相对误差perr来评价模型拟合的准确度,以相关系数CC来定义模型的有效预测步长。一般的,相关系数CC越接近1,则说明两组数据越接近,就时间序列的预测而言,若预测值与真实值的相关系数在1附近,则认为预测准确;若预测值与真实值相关系数接近0,甚至小于0,则认为预测效果很差。同时,本文选取0.99作为一个由相关系数CC定义模型有效预测长度的阈值,即将此阈值对应的预测长度定义为模型的有效预测长度,作为度量模型性能的指标。

Figure 1. The process of LPP modeling and algorithm
图1. LPP建模算法流程
若以 和
和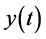 分别表示仿真实验的真实值和预测值,则这三种评价标准的定义表达式如下
分别表示仿真实验的真实值和预测值,则这三种评价标准的定义表达式如下
 (12)
(12)
式中,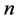 表示时间序列预测值的个数,
表示时间序列预测值的个数, 和
和 分别表示真实值和预测值的平均值。
分别表示真实值和预测值的平均值。
3.1. Logistic映射
Logistic映射表达式如下
 (13)
(13)
式中,取 ,此时系统具有混沌特性。取初始值
,此时系统具有混沌特性。取初始值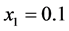 ,直接迭代10000步,去除前面1000个数据后选取不同训练样本进行仿真实验,实验结果见表1。
,直接迭代10000步,去除前面1000个数据后选取不同训练样本进行仿真实验,实验结果见表1。
从表1可以看出,LPP2模型能够有效的预测Logistic混沌时间序列,不同样本量的预测效果一致优于局域线性模型以及LPP1模型,尤其是在样本量为500、2000、4000以及8000时的MAE和perr的数量级相差十分的大。对样本量为4000的预测结果做进一步分析,图2是样本量为4000时不同模型真实值和预测值的图像以及其相应的绝对误差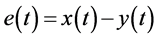 的图像,图3为相关系数CC随预测个数增加而变化的图像。
的图像,图3为相关系数CC随预测个数增加而变化的图像。
从图2可以看出,LPP2模型能够有效的预测Logistic混沌时间序列,预测精度高。而线性模型的预测值与真实值有较大偏差。从图3可以看出,线性模型预测值与真实值的相关系数同LPP2模型相比低很多,且随着预测步数的增加出现了负值,其多步预测性能随着预测步数的增加越来越差。表2给出了在0.99阈值下各模型预测Logistic混沌时间序列的有效预测长度。从表2可以看出,LPP2模型的有效预测长度最大。
3.2. Henon映射
Henon映射表达式如下
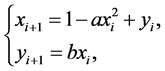 (14)
(14)
式中,取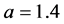 ,
, ,此时系统具有混沌特性。取初始值
,此时系统具有混沌特性。取初始值 ,
,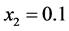 ,直接迭代10,000步,去除前面1000个数据后选取不同训练样本进行仿真实验,实验结果见表3。
,直接迭代10,000步,去除前面1000个数据后选取不同训练样本进行仿真实验,实验结果见表3。
表3和表1结果是一致的,即采用方案2定阶的LPP2模型能够有效的预测Henon混沌时间序列,预测效果一致的优于线性模型以及LPP1模型。这表明LPP2模型能够很好的估计Henon映射的变化趋势并对其将来值进行预测。
同样,对样本量为4000时的Henon混沌时间序列的预测性能做进一步分析。结果见图4与图5。
从图4可以看出,LPP2模型能够有效的预测Henon混沌时间序列,预测精度高。而线性模型的预测值与真实值有较大偏差。从图5可以看出,线性模型预测值与真实值的相关系数CC同LPP2模型相比低很多,且随着预测个数的增加出现了负值,故认为线性模型的预测性能比LPP2模型差的多。表4给出了各模型预测Henon混沌时间序列的有效预测长度。从表4可知,LPP2模型具有最好的预测效果。
3.3. Lorenz系统
Lorenz系统表达式如下

Table 1. The comparative results of different samples of Logistic time series
表1. Logistic映射混沌时间序列不同数量训练样本的预测误差
注:记号“--”表示数值大于10。

Table 2. The effective length of forecasting in different training samples of Logistic time series
表2. Logistic混沌时间序列不同数量训练样本的有效预测长度

Table 3. The comparative prediction error of different samples of Henon time series
表3. Henon映射混沌时间序列不同数量训练样本的预测误差
注:记号“--”表示数值大于10。
 (a) 线性模型50步预测的真实值和预测值
(a) 线性模型50步预测的真实值和预测值 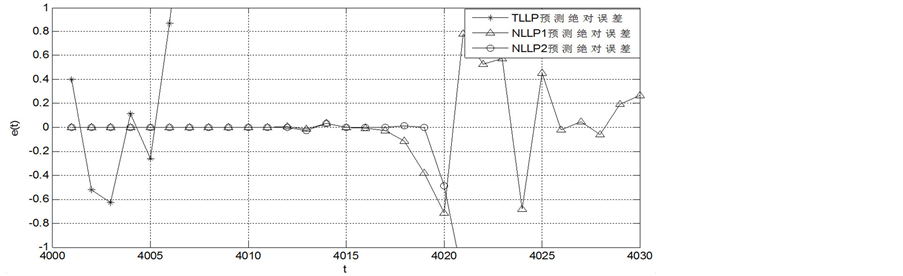 (b) 线性模型30步预测的绝对误差
(b) 线性模型30步预测的绝对误差  (c) LPP模型50步预测的真实值和预测值
(c) LPP模型50步预测的真实值和预测值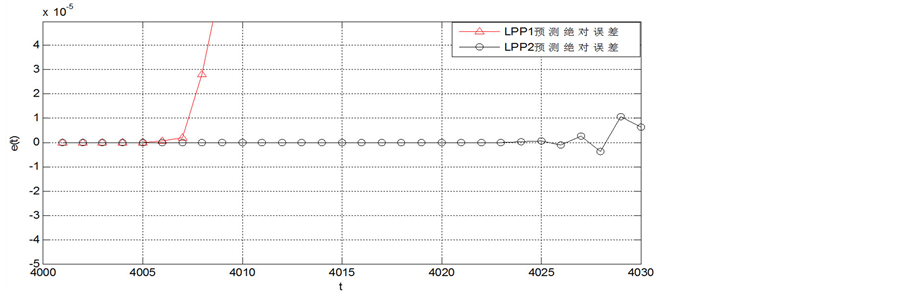 (d) LPP模型30步预测的绝对误差
(d) LPP模型30步预测的绝对误差
Figure 2. Results of Logistic time series multi-step prediction
图2. Logistic映射混沌序列的多步预测结果
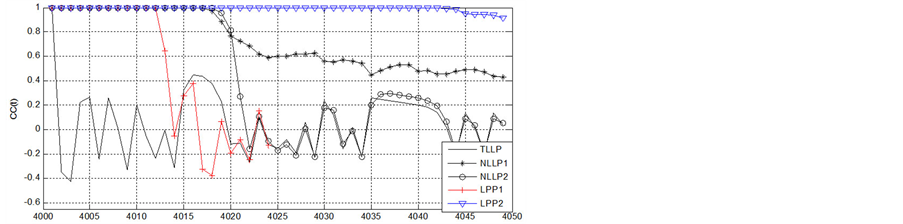
Figure 3. Trends in the correlation coefficient of different models of Logistic time series
图3. Logistic映射混沌序列在不同模型下的相关系数变化趋势
 (a) 线性模型50步预测的真实值和预测值
(a) 线性模型50步预测的真实值和预测值  (b) 线性模型30步预测的绝对误差
(b) 线性模型30步预测的绝对误差  (c) LPP模型50步预测的真实值和预测值
(c) LPP模型50步预测的真实值和预测值 (d) LPP模型30步预测的绝对误差
(d) LPP模型30步预测的绝对误差
Figure 4. Results of Henon time series multi-step prediction
图4. Henon映射混沌序列的多步预测结果
 (15)
(15)
式中,取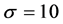 ,
, ,
,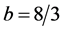 ,此时系统具有混沌特性。式(15)的Lorenz模型,只考察分量
,此时系统具有混沌特性。式(15)的Lorenz模型,只考察分量 的预测。假定初值条件
的预测。假定初值条件 ,
, ,
, ,取步长
,取步长 ,利用四阶Runge-Kutta产生长度为10,000的时间序列,去除前面1000个数据后选取不同训练样本进行仿真实验,实验结果见表5。
,利用四阶Runge-Kutta产生长度为10,000的时间序列,去除前面1000个数据后选取不同训练样本进行仿真实验,实验结果见表5。

Figure 5. Trends in the correlation coefficient of different models of Henon time series
图5. Henon映射混沌序列在不同模型下的相关系数变化趋势

Table 4. The effective length of forecasting in different training samples of Henon time series
表4. Henon混沌时间序列不同数量训练样本的有效预测长度

Table 5. The comparative prediction error of different samples of Lorenz time series
表5. Lorenz系统混沌时间序列不同数量训练样本的预测误差
从表5可以看到,在样本量为1000时,TLLP模型的预测效果最好,而其它复杂方法效果不好。为了分析原因,做出 的图像,见图6。从图6可以看出,要预测的点周围基本没有邻域点,这是导致预测效果差的主要原因。这也是局域法的一大缺点,即无法对相空间中没有出现过的点进行有效的预测。在样本量为2000、4000和8000时的预测效果LPP1模型的预测效果优于LPP2模型,也优于局域线性模型,但效果相差不大。再次观察图6,可以看出对Lorenz混沌时间序列重构后,具有很强的局域线性特性,这也是局域线性模型预测效果好的原因。尽管如此,LPP模型仍能有效的估计Lorenz系统的变化趋势。图7和图8是样本量为4000时不同模型的预测结果。
的图像,见图6。从图6可以看出,要预测的点周围基本没有邻域点,这是导致预测效果差的主要原因。这也是局域法的一大缺点,即无法对相空间中没有出现过的点进行有效的预测。在样本量为2000、4000和8000时的预测效果LPP1模型的预测效果优于LPP2模型,也优于局域线性模型,但效果相差不大。再次观察图6,可以看出对Lorenz混沌时间序列重构后,具有很强的局域线性特性,这也是局域线性模型预测效果好的原因。尽管如此,LPP模型仍能有效的估计Lorenz系统的变化趋势。图7和图8是样本量为4000时不同模型的预测结果。
从图7可以看出,线性模型和LPP模型均能够有效的预测Lorenz混沌时间序列。从图8可以看出,各模型预测值与真实值的相关系数CC均接近于1,故认为各个模型的预测性能差不多。表6给出了各模型预测Lorenz混沌时间序列的有效预测长度。从表6可以看出,LPP2模型的有效预测长度是最长的,可以对Lorenz混沌时间序列进行长期预测,而局域线性模型和LPP1模型的有效预测长度相比就小很多。表7给出了对3种典型混沌时间序列不同样本量的不同模型的有效预测长度的均值±标准差。从表7可以看出,LPP2模型的预测效果是最好的,有最长的平均有效预测长度和小的标准差。

Figure 6. The resulting curve of standard test systems of Lorenz model point image
图6. Lorenz模型点图像标准试验系统结果曲线
 (a) 线性模型50步预测的真实值和预测值
(a) 线性模型50步预测的真实值和预测值  (b) 线性模型50步预测的绝对误差
(b) 线性模型50步预测的绝对误差  (c) LPP模型50步预测的真实值和预测值
(c) LPP模型50步预测的真实值和预测值 (d) LPP模型50步预测的绝对误差
(d) LPP模型50步预测的绝对误差
Figure 7. Results of Lorenz time series multi-step prediction
图7. Lorenz系统混沌序列的多步预测结果

Figure 8. Trends in the correlation coefficient of different models of Lorenz time series
图8. Lorenz系统混沌序列在不同模型下的相关系数变化趋势

Table 6. The effective length of forecasting in different training samples of Lorenz time series
表6. Lorenz混沌时间序列不同数量训练样本的有效预测长度

Table 7. Means and standard of the effective length of forecasting in three typical chaotic time series
表7. 三种典型混沌时间序列有效预测长度的均值与标准差
4. 结论
本文提出的LPP混沌时间序列预测模型,通过使用局域非线性方法,很好地逼近了混沌时间序列的非线性特性。仿真结果表明该方法是非常有效的,尤其是LPP2模型,对混沌时间序列的预测精度较高,有较长的有效预测长度,预测性能稳定,在小样本量的情况下,LPP2模型的预测效果显著优于局域线性模型。同时结果表明,LPP2模型将3种典型混沌时间序列的有效预测长度提升了一倍以上。LPP模型综合了局域法与线性模型的优点,算法简单高效,可以在不增加较大计算量的前提下大幅度提高预测精度,是预测混沌时间序列的一种新的有效尝试。
基金项目
国家自然科学基金(11471060);重庆市科委基础与前沿研究计划项目(cstc2014jcyjA40003);重庆市教委研究生教育教学改革研究项目(Yjg133029);重庆理工大学研究生教育教学改革研究一般项目(yjg2012208)。