1. 引言
在我国发电资源分布上,呈现出经济发展相对落后的西部地区资源丰富、经济较发达的东部地区资源贫乏的局面。因此,实施“西电东送”战略是应对我国不均衡的资源分布与生产力布局的客观要求,对加速调整我国的能源结构和东部快速经济发展、西部大开发战略都发挥着重大作用。因此实现我国大电网之间的互联可实现多方效益。目前,国外很多国家的电网均实现了全国电网的互联,比如北美、欧洲、巴西等。因此,实现大电网互联是世界范围内各个国家和地区电网发展的客观规律[1] 。
我国的电网互联经历了从城市小电网、省级电网、区域电网,再逐渐发展至全国联网的历程,电网规模随着互联进程的推进逐步扩大。当前,我国电网已经进入跨大区互联、特高压交直流混合输电阶段。按照电网规划,我国特高压交直流输电系统传输容量将提升至200 GW以上,实现西北、华北、华中和华东电网的互联,并且将覆盖大电源基地以及负荷中心,从而形成覆盖17个省级行政区的特高压电网[2] 。跨区大电网的互联能够极大提升我国大型能源基地以及清洁能源的集约高效开发利用,大力促进我国电力能源结构的优化调整、大气污染的加速治理以及节能减排目标的提前实现[3] 。
研究跨区互联大电网的安全稳定运行极为重要,工程中为节约成本通常采用计算机仿真对大电网的运行特性进行分析计算[4] 。其中机电暂态仿真主要对大电网整体的稳定性进行计算分析,为确定合理的电网结构及参数提供依据。与机电暂态仿真不同,电磁暂态仿真主要针对局域电网的动态特性进行研究[5] ,如电力系统过电压计算、绝缘配合、次同步谐振、谐波分析、保护及控制装置等的分析计算;对传统机电暂态仿真不能模拟的直流输电中的电力电子设备的开关特性电磁暂态仿真也能够详细模拟[6] 。然而,我国电力系统数据主要是沿用机电暂态仿真软件格式填写记录的,电磁暂态数据匮乏[7] 。故需将机电暂态数据转换为电磁暂态数据,才能对交直流电网进行更为详尽的仿真[8] 。旨在解决上述问题,本文创先对PSASP机电暂态模型向PSCAD电磁暂态模型转换的方法进行研究,具有重要的工程实际意义。
2. 潮流数据转换可行性分析
仿真计算中的数值积分算法、潮流迭代解法和元件的模型,PSASP和PSCAD两个软件有所不同,但是仿真计算结果均是对相同网络电气特性的描述。进行数据转换过程中,机电暂态模型和其对应的电磁暂态转换模型的仿真本质上均为对相同电力网络电气特性的反应,因此如果两个软件的仿真曲线的发展趋势相同,尽管存在一些差异,也能够验证模型转换的正确性和有效性[9] -[16] 。
电流和电压之间,在电网络理论中存在如下关系:
 (1)
(1)
写成向量形式,如下式:
 (2)
(2)
欲求解上式中电力网络的节点电流,由于网络为已知网络,其节点导纳矩阵为已知量,故只需求解出电力网络的节点电压。求解完毕,便能够得到电力网络中的功率分布,因而得到了网络的潮流分布。
2.1. PSASP潮流计算
PSASP软件中电力网络稳定运行状态下各电气参数的求解,需要给定电网参数与结构、发电机与负荷等元件的运行状态。一般待求解的运行参数有各个母线节点的电压相角与幅值、各个支路的有功与无功功率及电力网络的功率损耗等。一般给定的运行参数包括网络中平衡节点的相角和电压、枢纽点的电压、各个电源的功率、负荷的功率等。
根据以上各未知量和已知量,列出如式(1)的节点方程,便可对潮流计算进行求解。由于潮流方程为非线性方程,需要利用迭代算法对方程组进行求解。在迭代过程中可能会出现迭代不收敛的问题,因此PSASP提供了多种迭代求解算法以保证其计算过程的收敛,如牛顿法(功率式)、PQ分解法、牛顿法(电流式)、最佳乘子法、PQ分解转牛顿法等等[17] 。
2.2. PSCAD潮流计算
与机电暂态仿真潮流计算略有不同,PSCAD仿真软件基于EMTP理论开发而出,其潮流计算需要事先设置给定的电压幅值及有功功率或有功及无功功率或其他条件,然后通过调节电流的幅值和相角进行不断的稳态解迭代求解,直至符合给定的条件停止。计算开始时刻参数变量值设为0,然后依据设定的元件参数,对网络变量进行逐步调整,直至达到设置的给定要求。
PSCAD采用联立求解法进行潮流求解,需要将包括电力电子设备的所有交流系统和直流系统的运行状态方程全部列出,然后利用联立求解方法计算出网络中所有未知量的值,直到满足给定的要求。
综上所述,软件PSASP和PSCAD的潮流计算方法存在不同,潮流求解算法、迭代算法等均有差异[7] ,但是从本质上分析两种软件的潮流求解过程均是对式(1)的求解。因此从潮流数据转换角度来分析,PSASP模型向PSCAD转换具有可行性。
3. 动态模型转换可行性分析
机电暂态仿真软件PSASP的仿真步长较长,不能达到电磁暂态过程仿真的要求,尤其是包含大量电力电子开关设备的直流输电系统的电磁暂态动态特性。而电磁暂态仿真软件PSCAD的仿真步长短,对交流或直流系统电磁暂态动态特性能够模拟得很详尽[18] 。两种软件的数值求解方法也有一些不同,PSCAD相对于PSASP的数值求解结果,有着更高的精度和更小的误差。由于两种软件中构建的模型存在差异,因此很难详细分析两种软件对同一网络的仿真动态波形图,而对软件转换的定量分析需要保证两种软件的仿真曲线变化一致。但是由于两种软件仿真研究的侧重点存在不同,PSCAD重点研究电力网络发生故障或操作后产生的过电压和过电流现象,而PSASP重点研究电力网络受到扰动后发电机转子的运行状态和母线节点电压的变化情况。因此本文此处可不需定量分析两种软件动态模型转换的可行性,而从物理意义出发对转换可行性进行分析[19] 。所以通过分析PSASP软件和PSCAD软件中动态模型的仿真结果的发展趋势一致即可认为两种软件在动态模型转换上具有可行性。
(1) 发电机模型转换可行性分析
两种软件动态模型仿真研究的侧重点存在差异,尤其体现在发电机模型。发电机模型在PSASP软件中为6阶模型[20] ,不计转子转速对输出功率的影响以及定子绕组的电磁暂态过程,因此对于发电机详细的动态特性不能完全精确地进行模拟。而发电机模型在PSCAD软件中为8阶模型,考虑了转子转速对功率的影响以及定子绕组的电磁暂态过程[21] ,因此能够对于发电机详细的动态特性能完全精确地进行模拟。虽然两种软件发电机模型存在上述不同,但是这些差异对本文提出的方法影响不大,因为从发电机及网络体现的动态特性曲线的发展趋势来看,两种软件的发展趋势可以达到一致。
(2) 变压器模型转换可行性分析
变压器在两种软件中的模型不完全相同,但是其数值求解方法基本相同。变压器模型在PSASP软件中需要提供变压器零序参数,而在PSCAD软件中软件自身可以根据选择出的变压器接线方式计算出变压器的零序参数[22] 。本文在进行模型转换时,需要根据PSASP软件的变压器的绕线及接地方式,对应的生成相应的PSCAD变压器模型的接线设置。
(3) 线路模型转换可行性分析
PSASP采用Π型集中参数模型,PSCAD也提供了Π型模型、Bergeren模型和频率特性模型。因此,两种软件中的线路模型所体现出来的物理特性可以达到一致。用户可以根据实际要求对线路转换模型进行选择。
(4) 负荷模型转换可行性分析
负荷模型在PSASP软件体现为恒定阻抗、恒定电流、恒定功率以及感应电动机的组合,在PSCAD中也提供了一系列的恒定负荷和可变负荷,包括阻性、感性、容性负荷及感应电动机模型[23] ,因此能满足两种软件负荷动态模型的转换。
由以上分析可知,尽管PSCAD与PSASP存在一些差异,但是差异的产生是由于PSASP和PSCAD软件中的算法和模型存在不同的原因,而不是系统动态特性本质上的不同[24] 。因此电力网络在同样的运行工况下体现出的发展趋势与动态特性大体上一致即可验证模型转换在动态模型上的可行性。
4. PSASP与PSCAD共有模型转换等值计算
4.1. PSASP与PSCAD暂态参数
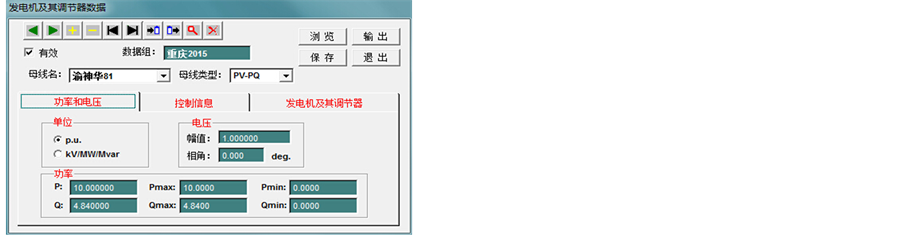
发电机模型在软件PSASP中的机电暂态参数如图1所示,在软件PSCAD中的电磁暂态参数如图2所示。
4.2. 模型转换等值计算
(1) 发电机名称(Machine name)
PSCAD中的发电机命名为PSASP中发电机所在母线的名称;其中PSASP发电机所在母线的名称,为读取PSASP中发电机及其调节器数据中的“母线名”字段的值;然后,写入PSCAD中发电机“Machine name”字段下。
(2) 额定相电压有效值(Rated RMS Line-to-Neutral Voltage)
读取PSASP发电机及其调节器数据中“功率和电压(幅值)”字段值,经换算写入PSCAD中“Rated RMS Line-to-Neutral Voltage”字段下;同步发电机为了消除3次谐波和降低绝缘水平,一般采用星型连接方式,线电压不等于相电压;换算规则如下。
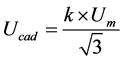 (3)
(3)

 (a) (b)
(a) (b) (c)
(c)
Figure 1. PSASP generator and regulator electromechanical transient parameters; (a) power and voltage; (b) parameters; (c) generator
图1. PSASP发电机及其调节器机电暂态参数;(a)功率和电压;(b)参数组;(c)发电机


 (a) (b) (c)
(a) (b) (c)
Figure 2. PSCAD generator and regulator electromagnetic transient parameters; (a) basic configuration; (b) basic data; (c) generator data
图2. PSCAD发电机及其调节器电磁暂态参数;(a) 基本配置;(b) 基本数据;(c) 发电机数据
式中:Um表示PSASP发电机及其调节器数据中“母线名”字段母线的额定电压值,单位kV,三相线电压;k表示PSASP发电机及其调节器数据中“功率和电压(幅值)”字段值,当为“0”时,默认取值“1”;Ucad表示写入PSCAD发电机中“Rated RMS Line-to-Neutral Voltage”字段值,单位kV,相电压。
(3) 额定线电流有效值(Rated RMS Line Current)
读取PSASP发电机及其调节器数据中“发电机及其调节器(额定容量)”字段值,经换算写入PSCAD中“Rated RMS Line Current”字段下;同步发电机为了消除3次谐波和降低绝缘水平,一般采用星型连接方式,线电流等于相电流;换算规则如下。
发电机的相电压Up:
 (4)
(4)
发电机的相电流Ip:
 (5)
(5)
代式(4)入式(5)中:
 (6)
(6)
PSCAD中发电机的线电流Icad:
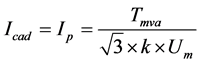 (7)
(7)
式中:Tmva表示PSASP发电机及其调节器数据中“发电机及其调节器(额定容量)”字段值,单位MVA;当为“0”时,默认等于“100”;Um表示PSASP发电机及其调节器数据中“母线名”字段母线的额定电压值,单位kV,线电压;k表示PSASP发电机及其调节器数据中“功率和电压(幅值)”字段值,当为“0”时,默认取值“1”;Icad表示写入PSCAD发电机中“Rated RMS Line Current”字段值,单位kA,线电流。
(4) 基准角频率(Base Angular Frequency)
工频频率为“50 Hz”,在PSCAD发电机中“Base Angular Frequency”字段下,写入工角频率“100 π” rad/s。
(5) 惯性常数(Inertia Constant)
读取PSASP发电机参数数据中“时间常数(TJ)”字段值,写入PSCAD发电机中“Inertia Constant”字段下。
(6) 电枢电阻(Armature Resistance)
读取PSASP发电机参数数据中“定子电阻”(Ra)字段值,经换算写入PSCAD发电机中“Armature Resistance”字段下,换算规则如下。
PSASP数据中标幺值Ra有名化,单位Ω:
 (8)
(8)
Ra有名值在PSCAD软件中标幺化:
 (9)
(9)
代式(8)入式(9)得:
 (10)
(10)

Table 1. Generator reactance parameters in PSASP and PSCAD
表1. PSASP和PSCAD中发电机电抗参数

Table 2. Generator time parameters in PSASP and PSCAD
表2. PSASP和PSCAD中发电机时间参数
式中:Raasp表示PSASP发电机参数数据中“定子电阻”字段值;Sp表示PSASP中发电机参数数据中“标幺值基准信息”字段的值,单位MVA,当为“0”时,默认为PSASP中系统基准容量SB,通常为“100”;Tmva表示PSASP发电机及其调节器数据中“发电机及其调节器(额定容量)”字段值,单位MVA;当为“0”时,默认等于“100”;Racad表示写入PSCAD发电机中“Armature Resistance”字段下的值。
(7) 发电机其他参数
发电机电抗参数如d轴同步电抗、q轴同步电抗等参数的等值计算同发电机电枢电阻Ra的计算过程,只需将式(10)中的电枢电阻对应参数替换即可,本文此处略写,表1所示为PSASP和PSACD软件中发电机电抗参数名称、参数字符和在PSCAD中的参数存放字段。
由于发电机的时间参数不用进行换算,可将PSASP软件中对应的时间参数的数值填写入PSCAD对应字段内,其时间参数名称、参数字符和参数字段如表2所示。
5. 结论
本文从潮流数据和动态模型转换对PSASP模型向PSCAD转换的可行性进行了验证,并最后详细分析了PSCAD与PSASP共有的现有模型(包括发电机、变压器、输电线路、负荷及补偿器等)等值转换的数学分析,通过数学分析充分验证了PSASP模型向PSCAD转换的可行性。