1. 引言
在热力系统中,当承受高温高压的压力容器或管道发生破裂时,循环水从破口处向外快速喷放,高温高压水在上游和下游的压力差作用下闪蒸并变成汽水混合物,很快达到最大喷射流量,压差越大,喷放流量越大,当喷放的流量不再受下游压力变化(压差)的影响时,就达到了临界流 [1] 。压水堆发生破口喷放时,往往会发生两相临界流现象,由于两相之间存在着质量、动量和能量交换,两者之间存在着动力学的速度不平衡特性和热力学的温度不平衡特性,加上两相之间的界面捕捉极其复杂,因此,两相临界流的研究仍然是热工水力研究的热点方向 [2] 。再者,高压压力容器或管道发生破口时,喷放过程往往具有较大的破坏力和较高的危险性。因此,研究两相临界流的现象和机理模型对于准确分析和评价压水堆回路系统破口事故喷放过程、事故进程、制定合适的事故缓解措施具有十分重要的意义 [3] 。
反应堆失水事故的实验研究大大推动了两相临界流的模型开发,目前一些大型热工水力瞬态分析程序(如:RELAP5、RETRAN-3D、TRACE)都嵌入了临界流计算模型。在这些程序中,临界流模型的准确性直接影响临界流量的计算准确性,进而影响专设安全设施的设计容量、动作时间,影响事故缓解措施的有效性。
为此,清华大学阎义洲、臧希年采用RELAP5程序模拟了破口临界流实验,对RELAP5程序计算临界流的适应性做出了评价,其研究结果表明:RELAP5程序对临界流现象具有较准确的预测,RELAP5计算的卸压过程比实际情况更加迅速 [4] 。齐炳雪、俞冀阳重点分析了RELAP5-3D程序中的喷放系数对临界流模型计算准确性的影响,其结论为:RELAP5-3D程序在计算孔板及短管道时结果有较大偏差,因而该程序不适合短管道和孔板的临界流计算 [5] 。陈玉宙、杨春生等分别用现有物理模型进行了喷嘴临界流的计算,并对各种物理模型进行了客观的评价,结论是:在较高压力下,Henry-Fauske模型可较满意地预测临界流质量流率,但该模型在低压力下的计算值偏低 [6] 。目前,国内鲜有采用最新版的RETRAN-3D程序和RELAP5/MOD4.0进行模型研究,本文根据清华大学破口临界实验,分别用RELAP5/ MOD4.0程序和RETRAN-3D程序对实验进行模拟计算,分析和评价两个程序中临界流模型的适用性和准确性,比较两个程序在预测临界流现象时的差异。
2. 临界流模型介绍
2.1. RETRAN-3D程序所用临界流模型
RETRAN-3D程序通过设定接管处流量模型选项和调整临界流因子大小来计算临界流,即:根据上游控制体的焓值和压力、接管面积Aj(t)、用户定义的临界流因子Cj计算出临界流量Wcrit,并与采用动量方程计算出的接管流量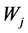 比较,从而判断是否发生临界流。若动量方程计算的流量大于临界流量,则程序会经比较判断后采用用户所选的临界流模型来计算该工况。
比较,从而判断是否发生临界流。若动量方程计算的流量大于临界流量,则程序会经比较判断后采用用户所选的临界流模型来计算该工况。
其中,在控制体内计算出流体的压力和内能,在接管处计算出流量,流量计算公式为:
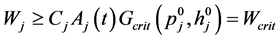 (1)
(1)
式中,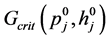 是根据滞止压力
是根据滞止压力 和滞止焓
和滞止焓 计算出的临界质量流率,用户可通过改变临界流因子
计算出的临界质量流率,用户可通过改变临界流因子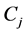 来计算不同形状(圆孔、方形孔等)流道的临界流大小。
来计算不同形状(圆孔、方形孔等)流道的临界流大小。
RETRAN-3D程序提供三种可选择的临界流计算模型来计算Wcrit:扩展的Henry-Fauske模型、Moody模型和热平衡态扩散模型 [7] 。这三个临界流模型的特点如下。
1) Henry-Fauske模型:程序中有两个Henry-Fauske模型计算公式,其中一个用于计算单相临界流,不考虑破口处的摩擦压降和提升压降,该模型是Sonic Choking模型的半经验改造模型,程序仅推荐在过冷状态下使用该模型;另一个用于计算两相临界流,程序默认的两相模型为均匀流模型,程序在Henry-Fauske模型中引入两相间的非平衡态模型——热不平衡参数N,用含气率表征两相热力学不平衡程度,当平衡含气率Xe > 0.14时认为两相处于热平衡状态,该模型在计算工质为0.345 MPa < p < 1.379 MPa、394.26 K < T < 449.81 K范围内的过冷水临界流时与实验有较好的符合度,其临界流的值由下面公式确定:
 (2)
(2)
其中: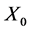 为滞止平衡含汽率,
为滞止平衡含汽率,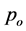 为滞止压力,
为滞止压力,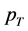 为喉部压力,
为喉部压力,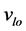 为液相比体积,
为液相比体积,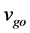 为气相比体积,
为气相比体积,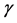 为比热容比,
为比热容比, 为喉部比体积。
为喉部比体积。
2) Moody模型:该模型假定两相处于热平衡状态,同时引入两相滑移速度模型,滑速比为: ,
,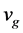 和
和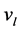 分别为气相比容和液相比容,结合总的能量方程和两相各自的连续性方程,该模型的临界流计算公式为:
分别为气相比容和液相比容,结合总的能量方程和两相各自的连续性方程,该模型的临界流计算公式为:
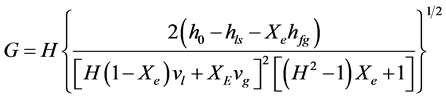 (3)
(3)
 (4)
(4)
其中: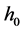 为滞止混合物比焓,
为滞止混合物比焓, 为液相饱和比焓,
为液相饱和比焓,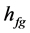 为汽化潜热,
为汽化潜热,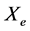 为平衡含汽率。
为平衡含汽率。
3) 热平衡态扩散模型:将临界流视为理想的等熵流动,该模型假设流体两相间无相对滑移,且处于热平衡状态,在计算过热蒸汽时推荐使用该模型,该模型的临界流流量为:
 (5)
(5)
其中: 为比体积,
为比体积, 为滞止混合物比焓,
为滞止混合物比焓,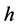 为流体在喉部比焓。
为流体在喉部比焓。
针对本实验模拟计算,选择RETRAN-3D程序的模型控制字“0”,即采用Henry-Fauske和Moody的联合模型进行模拟计算,在单相液体段采用Henry-Fauske模型,在两相段采用Moody模型,在发生临界流时,两相处于热平衡状态,且两相间具有滑移速度 [8] 。
2.2. RELAP5程序临界流模型
RELAP5程序为用户提供了平衡态和非平衡态的选项,程序在过冷状态下提供Bernoulli公式模型进行单相临界流模拟,而程序的两相临界流模型则是在TRAPP-RANSOM关系式的基础上得到的。为模拟不同破口面积下临界流量,程序提供了喷放系数的开放性输入 [9] 。
Bernoulli公式为单相不可压缩流体流动阻力特性公式,过冷状态的临界流速为:
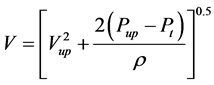 (6)
(6)
其中,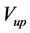 和
和 为上游的速度和压力,
为上游的速度和压力,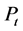 为破口处气泡发生点的压力。
为破口处气泡发生点的压力。
RELAP5程序假定破口处阀门或者接管中的空泡份额含量高于10−5时,程序会启动两相临界流模型。该程序在计算两相的临界流时也是采用Henry-Fauske模型,通过实验数据修正得到临界流流速为:
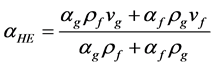 (7)
(7)
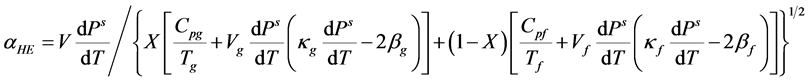 (8)
(8)
其中: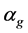 、
、 、
、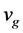 分别为气相空泡份额、气相密度以及气相比体积,
分别为气相空泡份额、气相密度以及气相比体积,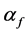 、
、 、
、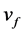 分别为液相空泡份额、液相密度以及液相比体积,
分别为液相空泡份额、液相密度以及液相比体积,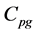 为气相比压热容,
为气相比压热容,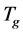 为气相温度,
为气相温度,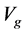 为气相速度,
为气相速度,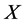 为含汽率,
为含汽率,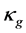 为等温气相压缩率,
为等温气相压缩率,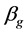 为气相热膨胀系数,
为气相热膨胀系数,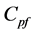 为液相比压热容,
为液相比压热容, 为液相温度,
为液相温度,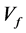 为液相速度,
为液相速度,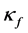 温液相压缩率,
温液相压缩率,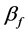 为液相热膨胀系数,
为液相热膨胀系数,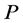 为流体压力。
为流体压力。
结合两相动量方程可以求出气相和液相流速 和
和 [10] 。
[10] 。
本次RELAP5程序对实验工况的模拟计算时选用Henry-Fauske模型选项。
3. 实验与计算描述
本文以清华大学高压容器卸压实验装置为计算分析数据,实验装置如图1所示,其实验模型的RELAP5节点图和RETRAN-3D节点图原理相同,如图1所示,共有3个部件组成:压力容器(划分为20个控制体)、阀门(110阀门)和大气环境(120时间相关控制体)。压力容器内装有15.0 MPa的过冷水,用阀门来模拟破口,破口直径为5 mm,阀门在0秒后立即开启,用时间相关控制体120来模拟大气环境,大气环境的压力为0.1013 MPa,温度为300 K。实验分为A、B两种工况,具体条件如表1所示。
4. 计算结果比较
4.1. 空泡份额结果比较
空泡份额的实验数据为离散点,程序计算结果为连续分布,取实验测点位置处空泡实验值与计算值进行比较,结果见图2~5所示。
破口发生后,压力容器内高温高压流体迅速向外排放,由于压力降低而发生闪蒸,空泡大量出现。
表1. 实验条件
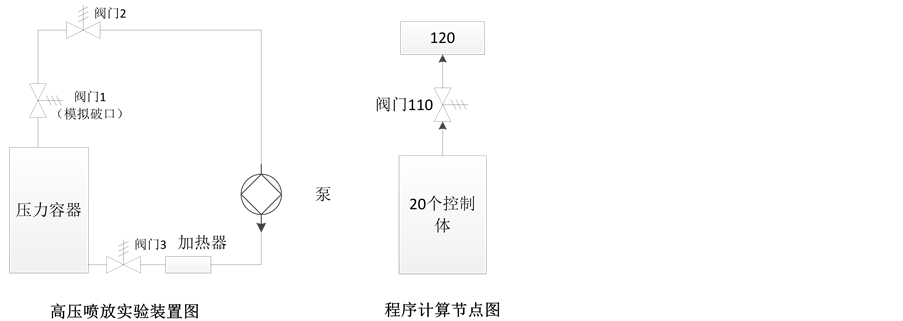
Figure 1. Diagrams of the experiment and code calculation node
图1. 实验装置与程序计算节点图

Figure 2. The upper void fraction comparison in the test A
图2. A实验工况上部空泡份额比较

Figure 3. The lower void fraction comparison in the test A
图3. A实验工况底部空泡份额比较

Figure 4. The upper void fraction comparison in the test B
图4. B实验工况上部空泡份额比较

Figure 5. The lower void fraction comparison in the test B
图5. B实验工况底部空泡份额比较
从实验与程序比较结果来看,两个程序计算出的空泡份额瞬态趋势基本与实验的趋势吻合;RELAP5程序计算出的压力容器上部控制体的空泡份额与实验值比较吻合,RETRAN-3D程序计算出的压力容器上部控制体的空泡份额与实验值存在一定程度的偏离;RELAP5程序计算出的压力容器底部控制体的空泡份额动态特性与实验值更接近且并能够长期执行计算,RETRAN-3D程序预测的压力容器底部控制体的空泡份额趋势与实验吻合但趋势单一且无法长期计算,600 s后因计算出现负压而终止计算。再者,由于A工况破口尺寸大于B工况,A工况泄压更快,因此A工况上部控制体空泡份额提前达到最大值1.0,底部控制体空泡份额更快稳定。两个程序从空泡份额总体趋势上基本与实验相吻合。
4.2. 压力比较
图6、图7给出了两个工况的压力分布。破口瞬间,压力容器顶部的压力急剧下降,6 s内快速降低到临界压力水平(A工况临界压力6.0 MPa,B工况临界压力8.0 MPa),两个程序都比较准确地预测出了这两个临界压力,但其中,A工况中RETRAN-3D程序预测的临界压力比实验值偏低0.2 MPa、RELAP5程序预测的临界压力比实验值偏低0.3 MPa,B工况中RETRAN-3D预测的临界压力比实验值偏高0.4 MPa、RELAP5预测的临界压力比实验值偏高0.1 MPa。当降低到临界压力后,RELAP5程序的泄压速率较实验值快,RETRAN-3D程序的泄压速率较实验值慢,其中,RETRAN-3D程序泄压速率与实验值比较接近。
4.3. 温度比较
图8和图9给出了两个工况下压力容器上部流体温度的变化结果。两个工况下程序计算出的压力容器顶部的温度瞬态趋势与实验趋势吻合,其中,RELAP5程序计算出的温度下降速度快,而RETRAN-3D程序计算出的温度下降速度慢,RETRAN-3D程序温度降低过程与实验值比较接近。
4.4. 剩余水装量比较
图10和图11分别给出了两个工况剩余水装量的变化结果。在喷放前期阶段,两个程序预测的剩余水装量均与实验值吻合,在喷放的末期阶段,两个程序的预测值均高于实验值,相比之下,RELAP5的结果更接近实验。

Figure 6. The upper void pressure comparison in the test A
图6. A工况上部压力比较

Figure 7. The upper void pressure comparison in the test B
图7. B工况上部压力比较
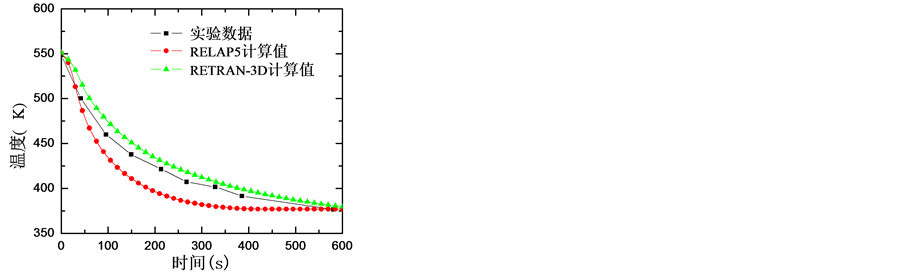
Figure 8. The upper void temperature comparison in the test A
图8. A工况上部温度比较

Figure 9. The upper void temperature comparison in the test B
图9. B工况上部温度比较

Figure 10. The remain water mass comparison in the test A
图10. A工况剩余水装量比较

Figure 11. The remain water mass comparison in the test B
图11. B工况剩余水装量比较
5. 小结
本文结合高压容器临界流喷放实验,采用RETRAN-3D程序和RELAP5程序进行了临界流喷放过程模拟计算,结果表明:
1) 两个程序均准确预测出了高压容器的临界压力大小和喷放过程趋势,其中,空泡份额、压力、温度、剩余水装量计算结果与实验结果趋势相吻合,数量值略有差异,其中,RELAP5程序空泡份额计算结果更接近实验,RETRAN-3D压力、温度、水装量计算结果更接近实验结果。
2) RELAP5计算临界流泄压速率比RETRAN-3D快,因此,RELAP5计算结果更偏于保守。
3) RETRAN-3D适合短期预测计算,RELAP5适合短期和长期的两相计算。
4) 在使用两个系统分析程序分析两相临界流时,需要结合类似的实验参考和经验来确定准确的临界流因子,从而确保计算结果的准确性。