1. 引言
随着信息社会迅速发展,人们对数据传输速率的要求越来越高,然而空中频谱资源有限,所以需要更有效地利用频谱资源[1] 。扩展的二元相移键控(Extended Binary Phase Shift Keying, EBPSK)是一种二元不对称调制[2] ,具有高频谱利用率,在加性高斯白噪声(Additive White Gaussian Noise, AWGN)信道中性能良好。
然而在高速移动坏境下,由于发射机和接收机之间的高速相对运动带来多普勒效应[3] ,使得传输信道快速时变,从而严重影响通信性能,典型以单径瑞利衰落信道为代表。经典的抗单径瑞利衰落技术如自适应信道均衡最小均方(Least mean squares, LMS)算法、递归最小二乘(Recursion Least Square, RLS)算法等,是基于基带的“星座图”均衡处理的,然而EBPSK调制信号不同于传统的调制信号,不易转换为传统意义上“星座图”,所以经典的抗单径瑞利衰落方法并不适用于EBPSK通信系统[4] -[6] 。在文献[3] 提出了两种用于EBPSK的抗单径瑞利衰落算法:自动跟踪判决门限算法和自动控制增益算法,在一定程度上提升了EBPSK系统在瑞利衰落信道下的传输性能,但其鲁棒性不强,深度衰落时改善效果不明显。因此,探索新的抗单径瑞利衰落技术对于EBPSK体制走向实用具有重大意义
本文首先介绍EBPSK调制与解调原理和单径瑞利衰落信道建模;然后提出两种基于EBPSK的抗单径瑞利衰落算法:插值估计衰落因子和插值估计判决门限;最后对这两种算法的误码率性能进行仿真和对比分析,结果表明,两种算法均提升了EBPSK系统在单径瑞利衰落信道中的传输性能。
2. 基本原理
2.1. EBPSK调制与解调
经典的二进制相移键控调制(Binary Phase Shift Keying, BPSK)是0~1对称的,能够完全抑制载波,但其频谱利用率低;而EBPSK将BPSK扩展为非对称调制,使已调波形近乎正弦波。EBPSK调制信号波形表达式如下[2]
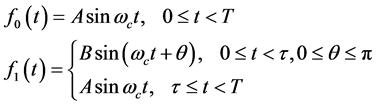 (1)
(1)
其中,T为码元持续时间,N为T内的载波周期个数; 为键控持续时间,K为
为键控持续时间,K为 内的载波周期个数且
内的载波周期个数且 。EBPSK调制信号的“0”和“1”码元波形差异小,即
。EBPSK调制信号的“0”和“1”码元波形差异小,即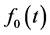 和
和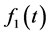 只在时段
只在时段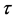 内不同。一类特殊的无限冲激响应(Infinite Impulse Response, IIR)数字带通滤波器可突出这种细小差异,称之为冲击滤波器,由一对共轭零点和至少两对共轭极点构成。通过其通带中心陡峭的陷波–选频特性,使EBPSK调制信号的相位跳变转化为寄生调幅冲击,突出待解调信号的差异[7] 。本文采用的冲击滤波器是单零点3极点,系统函数为
内不同。一类特殊的无限冲激响应(Infinite Impulse Response, IIR)数字带通滤波器可突出这种细小差异,称之为冲击滤波器,由一对共轭零点和至少两对共轭极点构成。通过其通带中心陡峭的陷波–选频特性,使EBPSK调制信号的相位跳变转化为寄生调幅冲击,突出待解调信号的差异[7] 。本文采用的冲击滤波器是单零点3极点,系统函数为
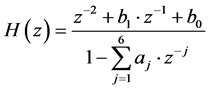 (2)
(2)
其中各系数的取值为:
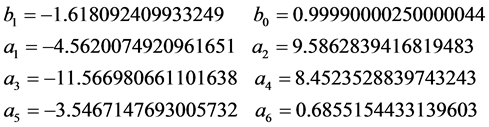
EBPSK调制信号经过冲击滤波器后的波形如图1所示(其中K = 2,N = 10),在码元“1”中,K个载波周期的相位跳变经过冲击滤波器后变为寄生调幅[8] [9] ,然后可采用包络检波和门限判决解调出“0”和“1”。因此可直接在中频上对发送码元进行判决,无需基带处理。
2.2. 单径瑞利衰落信道建模
如果发送一个余弦波,则接收端收到的单径衰落信号是一个调幅调相波,具有随机振幅和随机相位,从单一频率弥散成了一个窄带频谱。因此单径衰落信号实际上为窄带随机过程,其包络的一维统计特性服从瑞利分布,通常又称单径瑞利衰落。一般将Clarke模型[10] 作为单径瑞利衰落信道的数学模型,即:
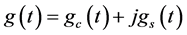 (3)
(3)
式中 ;N为不可分辨的传播路径数
;N为不可分辨的传播路径数
目,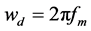 ,
,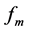 是最大多普勒频移,
是最大多普勒频移, 是衰减常数,
是衰减常数, ,
, ,
,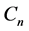 分别是第n径的随机路径到达角
分别是第n径的随机路径到达角
 (a)
(a)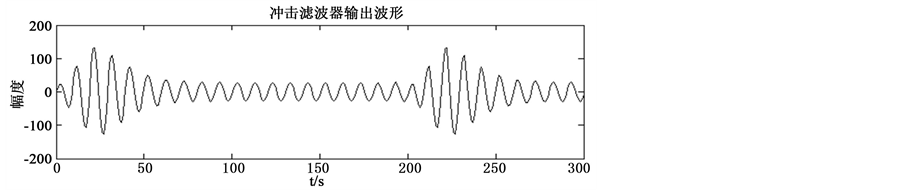 (b)
(b)
Figure 1. EBPSK waveform and filter output waveform
图1. EBPSK调制波形和滤波器输出波形
度、初始相位和增益, 和
和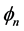 服从
服从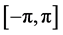 上均匀分布且相互独立。由贝尔实验室的William Jakes提出的Jakes模型对Clarke模型进行了简化,使得Clarke模型的收敛运算速度加快,Jakes模型 [11] 目前已被许多标准化组织接受,应用也最为广泛。Jakes假定具有相等功率的N个到达波的到达角满足
上均匀分布且相互独立。由贝尔实验室的William Jakes提出的Jakes模型对Clarke模型进行了简化,使得Clarke模型的收敛运算速度加快,Jakes模型 [11] 目前已被许多标准化组织接受,应用也最为广泛。Jakes假定具有相等功率的N个到达波的到达角满足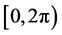 上的均匀分布,Jakes模型生成的第k次瑞利衰落的表达式由式(4)给出:
上的均匀分布,Jakes模型生成的第k次瑞利衰落的表达式由式(4)给出:
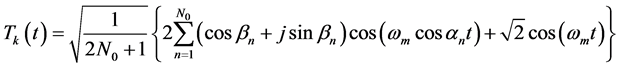 (4)
(4)
其中: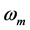 是最大多普勒频移,
是最大多普勒频移,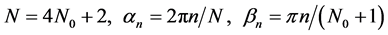 ,本文采用Jakes仿真模型 [10] 来对单径瑞利衰落信道建模。由于单径瑞利衰落信道的影响,EBPSK信号的幅度和相位受到干扰,而EBPSK特殊的冲击解调方式将相位跳变转变为寄生幅度跳变,使得单径瑞利衰落干扰转化为冲击滤波后信号包络的起伏,如图2所示,其中EBPSK调制信号参数为
,本文采用Jakes仿真模型 [10] 来对单径瑞利衰落信道建模。由于单径瑞利衰落信道的影响,EBPSK信号的幅度和相位受到干扰,而EBPSK特殊的冲击解调方式将相位跳变转变为寄生幅度跳变,使得单径瑞利衰落干扰转化为冲击滤波后信号包络的起伏,如图2所示,其中EBPSK调制信号参数为 ;单径瑞利衰落信道最大多普勒频移
;单径瑞利衰落信道最大多普勒频移 。
。
3. 抗单径瑞利衰落算法
单径瑞利衰落信道严重干扰了EBPSK系统的通信性能,所以要采用一定措施来抵抗单径瑞利衰落干扰。文献 [3] 提出了自动控制增益算法和自动跟踪判决门限两种算法,都对EBPSK系统在瑞利衰落信道中的传输性能有所改善。但是当衰落频繁且幅度出现较大波动时,两种算法在包络波谷出现局部信噪比恶化,导致突发误码。所以本文引入插值思想,提出两种新的抗单径瑞利衰落算法:插值估计衰落因子算法和插值估计判决门限算法。
3.1. 插值估计衰落因子算法
由2.2节可知,在单径瑞利衰落信道下,EBPSK经过冲击滤波器后信号波形包络会出现起伏波动,其表示为数学表达式:
 (5)
(5)
其中 为未经过单径瑞利衰落信道的EBPSK冲击滤波输出信号,
为未经过单径瑞利衰落信道的EBPSK冲击滤波输出信号,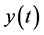 为单径瑞利衰落信道下EBPSK
为单径瑞利衰落信道下EBPSK
 (a)
(a)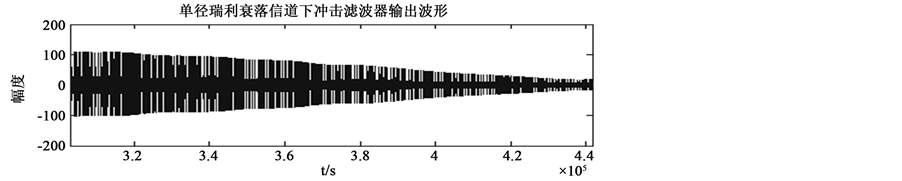 (b)
(b)
Figure 2. The waveform of EBPSK after impacting filter
图2. EBPSK调制信号经过冲击滤波器后的波形
冲击滤波信号,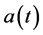 是衰落起伏因子,是EBPSK信号干扰经过单径瑞利衰落信道和冲击滤波后的信号包络起伏。
是衰落起伏因子,是EBPSK信号干扰经过单径瑞利衰落信道和冲击滤波后的信号包络起伏。
记码元“1”冲击幅度最高点的位置为dek,然后取每个发送码元冲击波形中dek位置的幅度值,将式(5)变为:
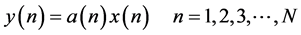 (6)
(6)
如果已知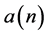 ,可以根据接收样本
,可以根据接收样本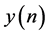 ,算出
,算出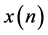 。然而传统的信道估计根据前段的发送训练序列估计
。然而传统的信道估计根据前段的发送训练序列估计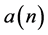 不可行,主要原因是
不可行,主要原因是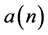 是一个时变量。所以本文引入插值思想来估计
是一个时变量。所以本文引入插值思想来估计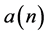 。
。
插值是一种重要的离散函数逼近方法,主要通过函数在有限个点处的取值,估算出函数在其它点处的近似值。常用的插值方法有线性插值、三次样条插值和立方插值。为了便于硬件实现和适应快速时变瑞利衰落信道,所以本文采用简单快速的线性插值方法:设已知函数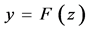 在自变量
在自变量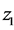 与
与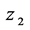 处的函数值为
处的函数值为 与
与 ,为了计算在自变量
,为了计算在自变量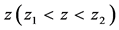 处的函数值
处的函数值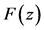 ,可以假定坐标平面上3点
,可以假定坐标平面上3点 ,
, 和
和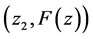 在一条直线上,利用公式
在一条直线上,利用公式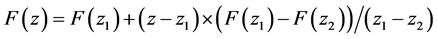 来计算
来计算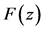 。根据线性插值原理,插值估计衰落因子算法的主要步骤为:
。根据线性插值原理,插值估计衰落因子算法的主要步骤为:
1) 在发送码元中,间隔k个插入训练码元“1”即 ,其中
,其中 为发送码元序列。
为发送码元序列。
2) 在接收端,根据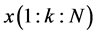 和
和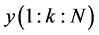 ,计算得到
,计算得到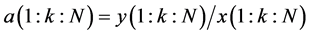 ,然后采用线性插值估计
,然后采用线性插值估计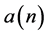 。
。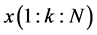 和
和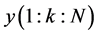 分别为训练码元的EBPSK调制信号通过和未通过单径瑞利衰落信道的冲击滤波器后冲击幅度值序列)。
分别为训练码元的EBPSK调制信号通过和未通过单径瑞利衰落信道的冲击滤波器后冲击幅度值序列)。
3) 最后计算得到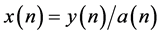 ,用于门限判决从而得到解调信号。
,用于门限判决从而得到解调信号。
为了精确估计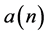 ,要求间隔k值越小越好,如图3所示,其中线性插值估计的归一化均方误差为−42.998 dB,
,要求间隔k值越小越好,如图3所示,其中线性插值估计的归一化均方误差为−42.998 dB,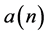 的估计值和实际值基本一致。
的估计值和实际值基本一致。
3.2. 插值估计判决门限算法
单径瑞利衰落信道使得EBPSK调制信号的冲击滤波输出包络出现起伏,尤其在深度衰落时起伏较明显,从而影响门限判决,出现突发误码。插值估计衰落因子算法是一种均衡方式,校正已失真的波形,使其恢复到未受瑞利衰落干扰的状态。而插值估计判决门限算法则是利用已失真波形,自动调整判决门
 (a)
(a) (b)
(b)
Figure 3. Interpolation estimation a(n)
图3. 线性插值估计衰落因子a(n)对比
限,跟踪包络起伏。同样引入3.1节提到的线性插值,对发送码元间隔k个插入训练码元,利用训练码元得到不同时刻的判决门限值,其中判决门限是码元“0”和码元“1”的冲击幅度的均值,所以设置训练码元为两个相邻的码元“0”和“1”,从而达到判决门限实时跟踪包络起伏的效果。插值估计判决门限算法主要思路如下:
1) 在发送码元中,间隔k个插入相邻两个训练码元“1”和“0”即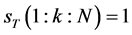 和
和 ,其中
,其中 为发送码元序列。
为发送码元序列。
2) 在接收端,根据接收到的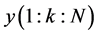 和
和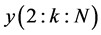 (分别为训练码元“1”和“0”的EBPSK调制信号经过冲击滤波器后冲击幅度值序列),进行线性插值估计,得到
(分别为训练码元“1”和“0”的EBPSK调制信号经过冲击滤波器后冲击幅度值序列),进行线性插值估计,得到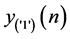 和
和 。
。
3) 根据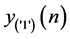 和
和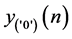 ,计算
,计算 得到判决门限
得到判决门限 ,最后利用实时判决门限进行门限判决,得到解调信号。
,最后利用实时判决门限进行门限判决,得到解调信号。
根据上述思路步骤仿真得到线性插值估计的实时门限,如图4所示,插值估计的判决门限T[n]基本跟踪上了EBPSK衰落起伏信号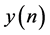 (在式(6)中提到)。
(在式(6)中提到)。
在插值估计判决门限算法和插值估计衰落因子算法中,间隔k值的选择非常重要,当信道衰落起伏波动趋势小,并且变化缓慢时,k可选择较大值,既能满足一定信息传输速率同时保证EBPSK解调性能。但当衰落频繁且幅度波动较大时,为了保证EBPSK系统能正常通信,需牺牲信息传输速率,使k值尽量小(3~5左右)。所以实用中,k值需要在EBPSK系统解调性能和信息传输速率之间进行折中。
4. 仿真结果
通过仿真实验来验证上述抗单径瑞利衰落算法的性能,并与自适应门限判决[12] ,自动增益控制[3] 及自动跟踪判决门限[3] 的性能进行对比。仿真参数如下:EBPSK参数:除了特别说明外,EBPSK信号调制参数一般均为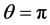 和A = B = 1,为简单起见,载波频率选取
和A = B = 1,为简单起见,载波频率选取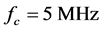 ,为了使EBPSK具有良好的频谱特性和解调性能[13] ,设置K = 2和N = 20;插值估计衰落因子和插值估计判决门限参数:线性插值估计,间隔k = 4;单径瑞利衰落信道参数:最大多普勒频移
,为了使EBPSK具有良好的频谱特性和解调性能[13] ,设置K = 2和N = 20;插值估计衰落因子和插值估计判决门限参数:线性插值估计,间隔k = 4;单径瑞利衰落信道参数:最大多普勒频移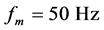 ;仿真结果如图5所示。
;仿真结果如图5所示。
由图5可得,在单径瑞利衰落信道中,自适应门限判决方法[12] 的误码率约为0.2,基本无法解调。其它4种抗单径瑞利衰落算法都对EBPSK的解调性能有所改善。其中插值估计判决门限算法最好,插值估计衰落因子算法略次之,自动控制增益系统算法劣于插值估计衰落因子方法,自动跟踪判决门限算法最差。自动跟踪判决门限算法[3] 的解调性能鲁棒性不强,在深度衰落处,门限无法完全跟踪包络起伏从
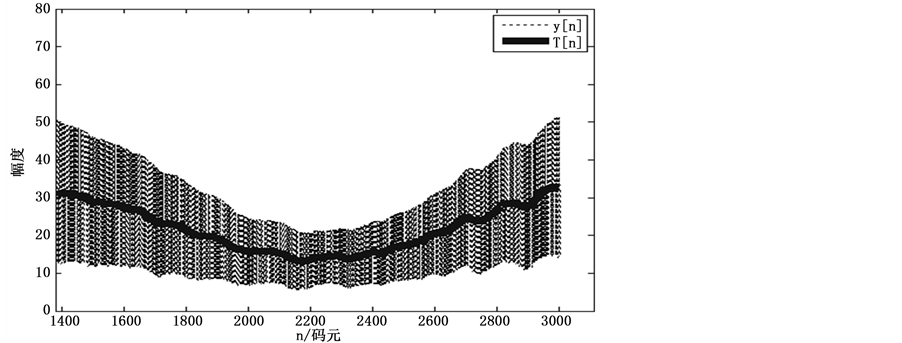
Figure 4. Interpolation estimation decision threshold tracking
图4. 插值估计判决门限跟踪情况

Figure 5. Performance comparison of EBPSK system with different resistance to single path Rayleigh fading
图5. EBPSK系统不同抗单径瑞利衰落算法性能对比
而出现误码。然而改进的插值估计判决门限算法能克服自动跟踪判决门限算法的不足,提升了EBPSK系统解调性能。在信噪比SNR=24 dB时,4种抗衰落算法误码率分别为 ,
,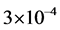 ,
, 和
和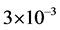 ,表明本文提出的插值估计判决门限算法和插值估计衰落因子算法在EBPSK系统中抗单径瑞利衰落的优越性。
,表明本文提出的插值估计判决门限算法和插值估计衰落因子算法在EBPSK系统中抗单径瑞利衰落的优越性。
5. 结束语
本文提出两种抗单径瑞利衰落算法用于提升EBPSK系统在高速移动环境下的传输性能。误码率对比仿真结果表明,相比于已有的基于EBPSK抗单径瑞利衰落算法,本文所提出的两种算法的抗单径瑞利衰落性能均有了一定的提升,其中插值估计判决门限算法最好。以后可借助本文算法,进一步研究基于EBPSK的多径衰落信道解调算法。
基金项目
国家自然科学基金资助项目(No.61271204);国家十二五科技支撑计划资助项目(No.2012BAH15B00)。