对三能级光纤激光器速率方程组的分析

Analyses of Rate Equations of Fiber Lasers with Three-Energy-Level Dopants

摘要: 对三能级光纤激光器的速率方程组进行了分析。在恒定泵浦功率的情况下，求解了三能级光纤激光器的速率方程组，获得了三能级光纤激光器的单位阶跃响应。并利用三能级光纤激光器的单位阶跃响应对三能级光纤激光器的输出特性进行了研究，研究表明：三能级光纤激光器的输出特性取决于三能级光纤激光器的阻尼比ξ。对于不同的阻尼比，可以得到不同阻尼的衰减振荡曲线以及过阻尼时的单调衰减曲线。当0 < ξ < 1时，三能级光纤激光器受激辐射的单位光子数密度将以频率ωd做衰减振荡。当ξ = 1或ξ > 1时，三能级光纤激光器受激辐射的单位光子数密度将无振荡单调上升。

Abstract: The rate equations of fiber lasers with three-energy-level dopants are anglicized. An expression of the unit step response of the fiber laser with three-energy-level dopants has been obtained from rate equations in a constant pump power. With these expressions, output characteristic of the fiber laser with three-energy-level dopants has been studied. The output characteristic of the fiber laser with three-energy-level dopants depends on its damping ratio, and the different damped oscillation curves and over-damped monotonic decay curves can be obtained for various damping ratio of the fiber laser with three-energy-level dopants. If 0 < ξ < 1, the photon density curves of stimulated radiation of the fiber laser will be a damping oscillation curves. If ξ = 1 or ξ > 1, the photon density curves of stimulated radiation of the fiber laser will be non-oscillating monotonic decay curves.

1. 引言

光纤激光器(Fiber Laser)是指用掺稀土元素玻璃光纤作为增益介质的激光器，目前已经成为重要的光源[1] -[4] ，大量的理论与实验研究表明，可以用速率方程组来研究光纤激光器的特性。迄今，除了采用数值方法来求解速率方程组外[5] [6] ，人们还对速率方程组进行了解析求解[7] -[9] 。例如，Chen [7] 与Zhang [8] 等人获得了掺杂三能级光纤激光器速率方程组的解析解，窦汝海[9] 等人利用三能级光纤激光器泵浦功率阈值的解析表达式对其阈值特性进行了具体分析。在本文中，我们在恒定泵浦功率的情况下，求解了三能级光纤激光器的速率方程组，获得了三能级光纤激光器的单位阶跃响应。并利用三能级光纤激光器的单位阶跃响应对三能级光纤激光器的输出特性进行了研究，结果表明：三能级光纤激光器的输出特性取决于三能级光纤激光器的阻尼比ξ。对于不同的阻尼比，可以得到不同阻尼的衰减振荡曲线以及过阻尼时的单调衰减曲线。当0 < ξ < 1时，三能级光纤激光器受激辐射的单位光子数密度将以频率ωd做衰减振荡。当ξ = 1或ξ > 1时，三能级光纤激光器受激辐射的单位光子数密度将无振荡单调上升。

2. 三能级光纤激光器的速率方程组

在三能级光纤激光器中，基质中有基态E₁、亚稳态E₂、激发态E₃三个能级，通过抽运过程能够以一定的抽运速率把处于基态E₁的粒子抽运到激发态E₃，而处于激发态E₃的粒子能够通过自发辐射跃迁到亚稳态E₂或基态E₁，处于亚稳态E₂的粒子能够通过自发辐射或受激辐射跃迁到基态E₁，处于基态E₁的粒子通过受激吸收也能够跃迁到亚稳态E₂。

根据激光理论，dt时间内从基态E₁泵浦到激发态E₃的粒子数密度：

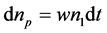(1)

其中w为泵浦抽运速率，n₁为处于基态E₁的粒子数密度。dt时间内从激发态E₃跃迁到基态E₁的自发辐射光子数密度：

(2)

其中A₃₁为自发辐射爱因斯坦系数，n₃为处于激发态E₃的粒子数密度。dt时间内从激发态E₃跃迁到亚稳态E₂的自发辐射光子数密度：

(3)

其中A₃₂为自发辐射爱因斯坦系数。dt时间内从亚稳态E₂跃迁到激发态E₃的粒子数密度：

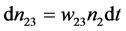(4)

其中为吸收速率，B₂₃为受激吸收爱因斯坦系数，u(ν)为光的辐射能密度，n₂为处于亚稳态E₂的粒子数密度。dt时间内从亚稳态E₂跃迁到基态E₁的自发辐射光子数密度：

(5)

其中A₂₁为自发辐射爱因斯坦系数。dt时间内从亚稳态E₂跃迁到基态E₁的受激辐射光子数密度：

(6)

其中为受激辐射速率，B₂₁称为受激辐射爱因斯坦系数。dt时间内从基态E₁跃迁到亚稳态E₂的受激吸收光子数密度：

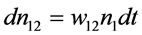(7)

其中为吸收速率，B₁₂为受激吸收爱因斯坦系数，u(ν)为光的辐射能密度。由式(1)~式(7)，dt时间内n₁的增量：

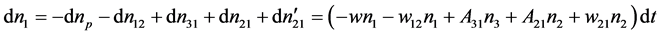(8)

由式(1)~式(7)，dt时间内n₂的增量：

(9)

设处于基态E₁和亚稳态E₂、激发态E₃的总粒子数密度为：

(10)

由式(8)~式(10)得描述亚稳态E₂的微分方程：

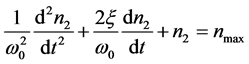(11)

其中，为三能级光纤激光器的固有频率；，为三能级光纤激光器的阻尼比；。

3. 分析与讨论

对于恒定泵浦抽运功率的三能级光纤激光器，w为常数。这种系统的输出特性取决于系统的阻尼比ξ，由于ξ ≠ 0。下面分别讨论0 < ξ < 1、ξ = 1、ξ > 1三种情况对应的输出特性。

3.1. 三能级光纤激光器的欠阻尼响应

当0 < ξ < 1，并输入单位阶跃函数时，系统的单位阶跃响应为：

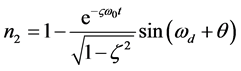(12)

其中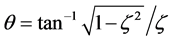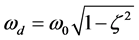，，这时n₂将以频率ω_d做衰减振荡。ξ越大，衰减越快，可见此时三能级光纤激光器处于欠阻尼状态。由式(5)、式(12)得：

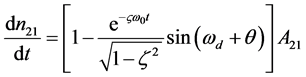(13)

这时单位时间内从亚稳态E₂跃迁到基态E₁的自发辐射的单位光子数密度将以频率ω_d做衰减振荡。

由式(6)、式(12)得：

(14)

这时单位时间内从亚稳态E₂跃迁到基态E₁的受激辐射的单位光子数密度将以频率ω_d做衰减振荡。

3.2. 三能级光纤激光器的临界阻尼响应

当ξ = 1，并输入单位阶跃函数时，系统的单位阶跃响应为：

(15)

这时n₂将无振荡单调上升，可见此时三能级光纤激光器处于临界阻尼状态。由式(5)、式(15)得：

(16)

这时单位时间内从亚稳态E₂跃迁到基态E₁的自发辐射的单位光子数密度将无振荡单调上升。

由式(6)、式(15)得：

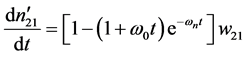(17)

这时单位时间内从亚稳态E₂跃迁到基态E₁的受激辐射的单位光子数密度将无振荡单调上升。

3.3. 三能级光纤激光器的过阻尼响应

当ξ > 1，并输入单位阶跃函数时，系统的单位阶跃响应为：

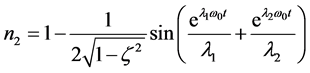(18)

其中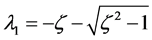，，这时n₂将无振荡单调上升，可见此时三能级光纤激光器处于过阻尼状态，近似一阶系统。由式(5)、式(18)得：

(19)

这时单位时间内从亚稳态E₂跃迁到基态E₁的自发辐射的单位光子数密度将无振荡单调上升。

由式(6)、式(18)得：

(20)

这时单位时间内从亚稳态E₂跃迁到基态E₁的受激辐射的单位光子数密度将无振荡单调上升。图1给出了不同阻尼比的三能级光纤激光器的输出特性曲线。

Figure 1. The output characteristic of fiber lasers with three-energy-level dopants

图1. 三能级光纤激光器的输出特性曲线

4. 结论

综上分析可以看出，三能级光纤激光器的输出特性取决于三能级光纤激光器的阻尼比ξ。对于不同的阻尼比，可以得到不同阻尼的衰减振荡曲线以及过阻尼时的单调衰减曲线。当0 < ξ < 1时，三能级光纤激光器受激辐射的单位光子数密度将以频率ω_d做衰减振荡。当ξ = 1或ξ > 1时，三能级光纤激光器受激辐射的单位光子数密度将无振荡单调上升。

基金项目

国家自然科学基金(批准号：11275089，11375081)和山东省自然科学基金(批准号：ZR2011FQ001)资助的课题。