1. 引言
在飞机飞行噪声测量技术中，基于麦克风阵列的运动声源定位技术是飞行噪声测量的核心技术。运动声源定位技术主要涉及阵列设计技术和麦克风阵列校准技术。飞机噪声问题正日益成为飞机设计中的重要问题，无论是国际民用航空组织(ICAO)，还是美国联邦航空局(FAA)的噪声适航条例，都已把飞机的噪声问题提高到与飞机飞行性能、安全性、可靠性等同等地位 [1] 。噪声诊断与测量系统作为气动噪声研究的试验平台，是必不可少的基础试验设备，为能准确分析飞机飞行噪声分布，需要对运动声源定位有一定的技术储备。为了定位的准确，需要进行校准试验研究，运动声源定位精度与校准方法有直接关系 [2] 。在本文中对运动声源定位消声室内校准方法研究进行了详细阐述。
2. 运动声源定位阵列
气动噪声通常为宽频噪声，因此设计的阵列需要同时满足对高低频信号的测量需求，在确定了阵列测量频率范围的情况下，设计阵列需要考虑的事项：为满足对低频声信号的高分辨测量，阵列的孔径要尽量增大。为满足对高频声信号的测量，需要尽量多的麦克风。阵列大小、阵元数目固定后，不同的阵列形式会有不同的输出结果，因此设计阵列时需要考虑阵元分布形式。
2.1. 运动声源阵列设计
阵列的设计必须满足宽频率范围工作要求。为满足对低频声信号的测量，阵列的孔径必须要大些，以便获得足够的分辨率。要想满足声信号最高频率的测量要求，麦克风分布空间要小，以便满足消除空间混淆对半波长的规范要求。综合考虑，需大量麦克风才能满足上述要求。
常见的阵列设计策略是对阵列进行非规则性或非周期性设计。阵列麦克风的数量N是影响峰值旁瓣大小的主导因素。旁瓣理论平均功率级相对于主瓣近似为10 log(1/N) + 3 dB。根据经验，旁瓣峰值一般不会超过平均值10 dB。因此，阵列设计策略的准则是：旁瓣峰值最小化，阵列的有效动态范围最大化。
2.2. 阵列设计流程
有效的阵列设计需要综合考虑设计策略和实际限制。基本流程如图1：首先确定性能需求：主要包含有测量频率范围、空间分辨率、最大旁瓣级、阵列摆放位置等；确定限制因素：阵元数目的限制、同步数采通道数目的限制、阵列架安放的有效位置、试验操作问题等；初步设计与性能评估；如果评估得到了不可接受的结果，则根据期望进行折衷调整。主要有两种解决方式：一是放宽性能需求，二是放宽限制因素；确定折衷方案后，便对阵列进行优化调节，这是一个迭代过程直到阵列的综合性能最佳。
3. 运动声源定位校准
作为噪声源定位的关键部件麦克风及麦克风阵列，为确保其性能指标及测量的准确度，需要对其进行校准。如图2所示。在实际测试的时候，整个系统可能存在如下问题，需要用户特别注意并作出相应
Figure 2. Chart of calibration of moving sound location
图2. 运动声源定位校准框图
的处理：安装在阵列上的麦克风，由于长时间处于实验环境中，性能会有所变化。所以通过这些麦克风采集到的声压值(实际为电压值)可能已经不能真实的反映声压特性，因而在使用之前，需要对其进行校准；用户通过数据采集系统(DAQ)采集到的只是电压值，而并非实际的声压值，因而需要给出采集到的电信号与麦克风所在位置声压之间的转换关系。这个转换关系包括两个因素：麦克风自身将声压信号转换为电信号时的灵敏度，这个值一般可以通过查阅其产品说明书获得；麦克风输出的电压值经由阵列电路会放大一定的倍数。
在完成所有的安装之后，由于麦克风的频率响应和灵敏度的不同、前置放大器、电缆的铺设、电源和信号调理器的频率响应影响、数据采集的输入、模拟抗混淆滤波器的影响、阵列架的加工误差以及与麦克风在阵列中的安装，会引起数据采集系统各测量通道间固有的相位差和幅值差 [3] 。通过前期的阵列研究，所有的麦克风相位性能一致，本次只进行阵列对运动声源定位的定性研究。
运动声源定位阵列与声源相对位置关系如图3所示，采用两个相互位置关系固定的点声源沿上方移动带移动，采用阵列进行数据采集，验证定位算法对不同位置关系声源、不同运动速度下的声源定位能力。声源从左端按照指定的速度移动到右端，通过先运动启动，后采集的流程进行运动声源数据采集。
Figure 3. The relative position relationship between the moving sound location array and the sound source
图3. 运动声源定位阵列与声源相对位置关系
4. 数据分析
对于移动的声源，声传递函数与时间有关，且测量的声压信号受到多普勒频移的影响。因此为了获得正确的、去除多普勒的声源信号，波束形成必须在时域中进行。对于固定的声源，可以对平均互谱矩阵应用固定的引导函数，对于运动声源，每个单独的采样必须有时间位移和与辐射时声源位置(速度)有关的振幅修正。这使得时域波束形成比频域波束形成有更多的时间损耗 [4] [5] 。
为了确定声源信号
与声压场
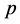之间的传递函数，我们须考虑均匀流
中运动单极子声源的波动方程：
(1)
除了声源位置
为时间的函数外，上式时域表达。传递函数
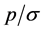可以通过两种情况的联合进行描述，无气流时，
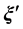位置处辐射的声经由
秒后到达
，但是由于亚声速气流
的对流作用，声同时传播至传声器位置
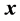，同时声传播至
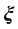处。因此，相对于媒质的声传播距离
为计算振幅减小量的正确距离。而且，用于确定放大系数的相对于媒质的声源速度为
，其中
为辐射时(即位置
处)的声源速度[6] [7] 。可以获得声源振幅与声压场关系的传递函数，使用传递函数作为引导函数，我们可以由测量的传声器信号中估计出运动声源的强度[8] [9] 。在辐射时刻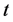
，对于给定的运动声源的扫描位置
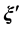和速度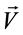
，可以使用延迟求和波束形成重构声源振幅
。
通过选择一系列等间隔时间
，就可以获得去除多普勒效应的声源信号。注意
时刻的传声器信号与测量次数
不相符(
为整数，
为采样间隔，见附录)。因此，为了获得期望时刻的传声器压力，对测量信号进行线形内插。对于等间隔时间
，如果声源是运动的，则传声器测得的信号将不是等间隔的，这对于所需的采样频率与低通滤波器产生影响。通过对重构的声源信号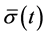
应用傅立叶变换可以获得去除多谱勒效应的声源谱，重构的声源信号导致与频率有关的声源振幅
。
通过静态声源定位程序无法区分两个声源的位置，只能看到声源出现的水平位置(Y轴坐标)，无法确定真实的位置(X坐标)，有严重的多普勒现象存在，必须通过移动声源定位校准程序处理数据[10] 。先进行FFT分析两个声源的单频点频率，频率分别为2368 Hz和2441 Hz。
图4所示是速度为25 cm/s时定位的极值坐标点为(−0.58, −0.18)和(−0.38, −0.18)。图5所示是速度为50 cm/s时定位的极值坐标点为(−0.22, −0.18)和(−0.02, −0.18)。两次定位点坐标差值都为20厘米，与两个点声源实际安装距离20厘米相同。通过自研的程序实现了运动声源的准确定位。
2368 Hz 2441 Hz
Figure 4. The results of the moving sound source localization program in speed 25 cm/s
图4. 速度25 cm/s时运动声源定位程序的处理结果
2368 Hz 2441 Hz
Figure 5. The results of the moving sound source localization program in speed 50 cm/s
图5. 速度50 cm/s时运动声源定位程序的处理结果
5. 结论
在消声室环境下，利用纵向运动移测架、横向运动移测架和固定安装的阵列，通过激光水平竖直测量装置精确测量阵列与运动声源的相对位置，模拟飞机在天空中飞跃条件下的运动声源定位测量，用静态声源定位程序处理数据无法获得声源的准确位置，用自研的运动声源定位程序处理噪声数据后，跟踪到了两个点声源的极值坐标位置，两个坐标点的位置差值与声源实际安装差值相同，声源纵向距离阵列垂直中心线距离与实际测量距离相同。通过此次消声室内运动声源定位测量，初步掌握了运动声源定位阵列设计及校准技术，为未来运动声源测量及飞机的飞行噪声源定位奠定基础。