1. 引言
水库群优化调度是复杂而传统的水资源系统分析问题。求解水库优化调度问题常采用线性规划、动态规划方法等优化方法 [1] 。几十年的应用表明，这些传统方法都存在一定局限性，无法有效解决水库群调度中“维数灾”问题 [2] 。对多维动态规划问题，可采用一些改进方法如离散微分动态规划(DDDP) [3] 、动态规划逐次渐进法(DPSA) [4] 以及逐次优化方法(POA) [5] 等，但这些算法存在结构复杂、效率低等缺点 [6] 。遗传算法(GA)是一种基于模拟自然基因和自然选择机制的寻优方法，在水库(群)优化调度领域中也得到了广泛的应用 [7] 。刘攀等(2006)对GA算法在水库调度中的应用问题进行了综述，认为遗传算法适用于传统方法难以求解的优化问题 [8] 。分布估计算法(EDA)是一种从“宏观”层面上建立数学模型的进化算法，具有比GA算法更好的全局搜索性能 [9] 。本文以百色、龙滩水库群为研究背景，考虑马斯京根流量演算，用GA和EDA算法求解防洪调度问题，并将所得结果进行比较研究，以此探讨水库群短期防洪优化调度问题。
2. 水库群短期防洪优化调度问题
2.1. 目标函数
对于确定性的水库群优化调度问题，可假定入库流量已知，求最优的水库调度策略，使得在满足各约束条件的前提下，获取的总效益最大化，采用水库群防洪优化调度最大削峰准则 [10] 为目标函数。将全部防洪水库群视为整体，充分发挥系统内各水库之间的库容补偿调节作用，使下游防洪控制点的最大流量最小，并提高整体的防洪效益。防洪调度目标函数的数学表达形式如下：
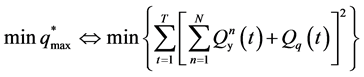(1)
式中：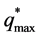
为下游站点的最大流量，m3/s；
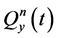为第n个水库出库流量经过演算到下游站点在时段t内平均流量，m3/s；
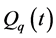为区间入流汇集到下游站点在时段t内平均流量，m3/s；T为调度时段总数；N为水库总数。
2.2 约束条件
1) 水量平衡约束
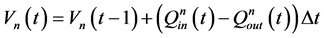(2)
式中：
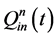和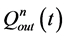
分别为t时刻第n个水库的入库和下泄流量；
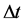为计算时段长度；
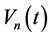为t时刻第n个水库的库容；
2) 水库库容约束
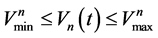(3)
式中：
和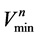
分别最小和最大允许库容；
3) 下游河道安全泄量约束
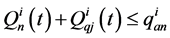(4)
式中：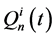
为n水库演算到i防洪控制点在t时段的流量；
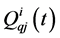为i河段在t时段的区间入流；
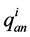为i防洪控制点的安全流量；
4) 水库泄流能力约束
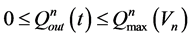(5)
式中：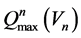
为n水库最大泄流能力函数，由该水库泄流能力曲线得出，即库容为
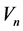时对应的水库最大下泄流量；
5) 泄量变幅约束
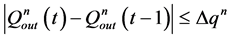(6)
式中：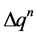
为第n个水库出库流量的最大变幅；
6) 边界条件约束
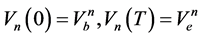(7)
式中：
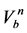和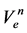
分别为第n个水库调度期初起调水位对应的库容和调度期末应回落到的水位对应的库容；
7) 马斯京根流量演算约束
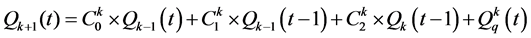(8)
式中：
、
、
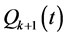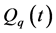分别为第k个马斯京根演算河段上、下断面第t时段的平均流量及演算河段的区间入流；
、
、
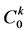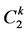为第k个马斯京根演算河段的演算参数。
2.3 滞时问题
在短期水库调度中，需要考虑马斯京根河段洪水演算。在某一个计算河段中，某时刻下游断面的流量不但与本时刻的上游断面流量有关，还与上一时刻该断面流量以及上断面流量有关，这样就产生了时间的滞后性。如果上游水库出库流量需要经过多个河段的马斯京根演算到下游某控制断面，滞后效应将更显著。文献 [11] 提出了马斯京根多河段流量演算线性方法，从数值方法角度证明了马斯京根演算法在连续多河段流量演算中如何产生滞时问题。水库群调度原本就有水库个数多而导致计算变量维数大、求解困难的问题，滞时问题的出现又增加了时间维度，加重了“维数灾”，最终使各类传统优化算法失效。
3. 优化算法
本文采用EDA和GA进行模型优化。上述优化模型的约束条件中，泄流能力约束和泄量变幅约束往往无法在优化调度模型的求解过程中直接应用。为形成容易求解的目标函数，一般的处理方式是向模型的目标函数中添加“惩罚函数”部分构成新的目标函数，即采用“惩罚函数”法，对不满足上述两种约束的时段进行“惩罚”。重新构建的目标函数为：
(9)
式中：E为总体目标函数，优化调度过程即为使E达到最小值；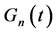
为n水库在t阶段的惩罚函数，具体形式见公式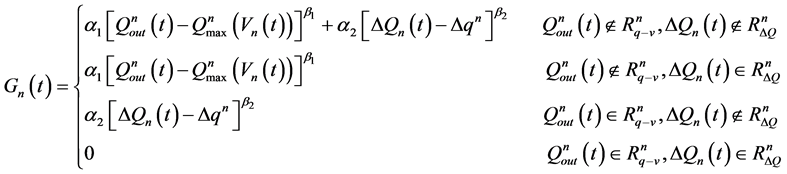(10)。
(10)
式中：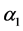
、
、
、
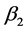为惩罚因子，均为正的常数，可根据实际需要做适当的调整；
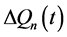为第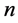
个水库的流量变幅，即
；
、
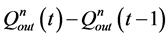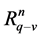分别为第
个水库流量可行域和流量变幅可行域。
3.1. 遗传算法(GA)
遗传算法是通过模仿生物的遗传、进化原理，按照“优胜劣汰”的法则，将适者生存与自然界基因变异、繁衍等规律相结合，采用随机搜索，以种群为单位根据个体的适应度进行选择、交叉和变异等操作 [8] 。在求解过程中，遗传算法从一个随机生成或者给定的初始群体开始，逐代寻找问题最优解，直到满足收敛判定条件或者设定的迭代次数为止，因此遗传算法在本质上也是一种迭代算法，并且已经证明，遗传算法能收敛于全局最优解 [12] 。
GA算法应用在水库群优化调度中，可直接采用各水库在调度期各时刻的库容或水位进行实数编码，每个染色体是由N*T(N个水库、T个时段)个基因组成。公式(9)的总体目标函数E直接作为适应度函数。GA算法的基本步骤如下：
1) 初始化种群：每个个体的单个基因由该位置对应的特定水库、特定时刻库容上下限范围内，即搜索空间内以均匀分布随机产生；
2) 适应度计算：计算各个染色体的目标函数即适应度函数；
3) 选择运算：水库群调度中选用比例选择和最优保存策略，个体适应度大的被选择的概率高；
4) 交叉运算：把两个父代个体的部分基因结构相互交叉、替换而生成新个体；
5) 变异运算：通过变异引入新的基因，保持种群的多样性，防止早熟；
6) 迭代终止：算法开始计算之前设置迭代终止的进化代数或者达到的精度要求，当迭代达到终止条件的时候停止迭代并输出最优解及对应的最优适应度值。
3.2. 分布估计算法(EDA)
分布估计算法(Estimation of distribution algorithm, EDA)是一种基于变量概率分布的随机搜索算法，有别于GA等其他进化算法，EDA算法不通过交叉、变异方式产生下一代群体。在进化过程中，针对当前代群体，首先根据个体适应度值的大小，以一定比例选择出若干适应度值较好的个体组成优势群体；然后根据优势群体的信息建立概率分布模型，通过概率模型对变量间的关系进行建模，并以此概率模型中抽样生成下一代群体。重复此过程，直到满足终止条件 [13] [14] 。EDA算法与GA算法的不同运算流程如图1所示。
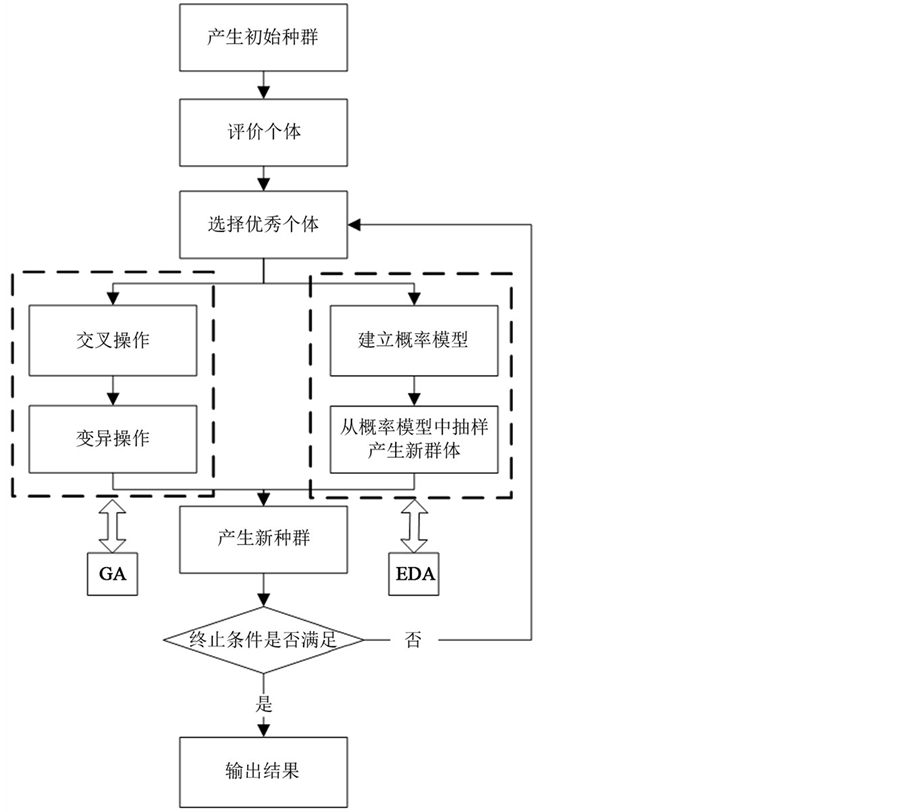
Figure 1. Flow chart of the GA and the EDA
图1. GA和EDA算法流程图
在EDA算法中，概率模型、抽样模型及替代模型是整个算法的关键。本文选取用有向图描述随机变量之间相关关系的高斯网络模型作为EDA算法的概率模型，从概率模型中抽样，并使用精英替代方法来产生新的种群替代上一代种群。
4. 实例研究
4.1. 百色、龙滩并联水库群概况
西江属于珠江干流，广西境内的西江水系面积为202,082 km2，占广西总面积的85.39%。西江流域位于亚热带华南季风气候区，受季风季候影响，降雨时空分布不均匀，降雨量年内变化大，4~9月降雨量可以占全年降雨量的80%左右。目前广西境内的西江流域面临的防洪形式十分严峻，尤其以广西境内西江下游梧州市的洪涝灾害问题最为严重。随着百色、龙滩等大型防洪水库的兴建及投入使用，以往严峻的防洪任务有了新的行之有效解决途径。西江流域的水库和防洪站点分布图如图2所示。
百色水库和龙滩水库是西江流域具有较大防洪库容的流域控制性水库，二者防洪库容之和占据了西江流域全部已建成防洪水库总库容的99%。百色和龙滩水库的主要参数见表1。百色水库是一座以防洪为主，兼有发
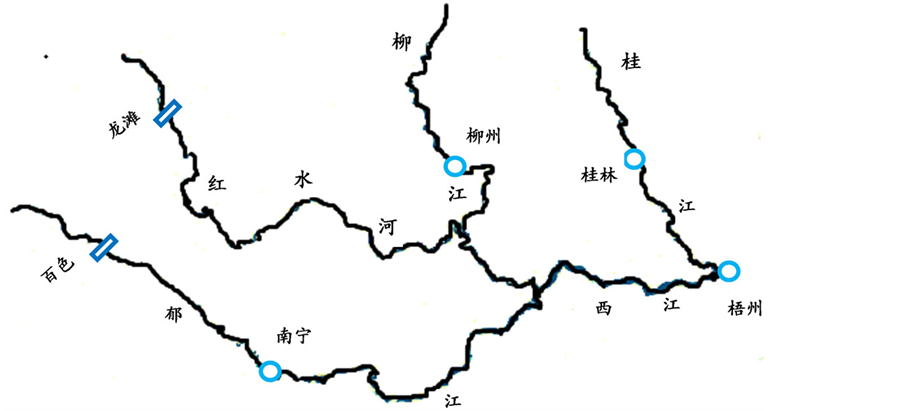
Figure 2. Flood control reservoirs and cities in the Xijiang River basin
图2. 西江流域防洪水库与城市分布图
Table 1. Parameters of the Bose and Longtan reservoirs
表1. 百色、龙滩水库主要参数
电、灌溉、航运、供水等综合利用效益的大型水利枢纽工程，防洪库容16.4亿m3，为不完全全多年调节水库。百色水库单库可将南宁市防洪标准由50年一遇提高到近100年一遇。龙滩水库是一座以发电为主，兼有防洪、航运和水产养殖等综合利用效益的工程，防洪库容50亿m3。龙滩的调洪作用主要是对以上中游来水为主的西江全流域型大洪水进行调节，可使梧州100年一遇的洪水削减为50年一遇。本次研究的主要任务就是将百色和龙滩水库进行联合调度，在满足下游河道安全、不降低自身防洪标准的前提下，尽可能的削减下游梧州防洪控制站点的洪峰流量。
由于百色、龙滩水库坝址距离梧州都有上百公里远，洪水传播时间长。百色、龙滩到梧州的洪水传播时间分别为120小时和132小时。考虑到出库流量的马斯京根河道演算，经计算在第t小时百色的出库流量演算到梧州站时主要组成了t + 140~t + 270这130个小时的部分流量，t小时龙滩出库流量演算到梧州站时主要组成了t + 120~t + 240这120个小时的部分流量。以龙滩水库为例，0时刻单位出库流量经马斯京根演算到下游梧州站，梧州站的流量过程如图3。
4.2. 结果对比分析
以西江流域某一场百年一遇设计洪水过程流量资料为输入数据，以1小时为计算时段长，西江下游梧州站
最大洪峰削减效果为目标，建立西江流域百色–龙滩水库群联合防洪优化调度模型。利用GA和EDA算法分别对调度模型进行求解。梧州站百年一遇洪峰流量为52,700 m3/s。设置种群数为80，迭代终止代数为100代，运行10次。对比两种算法的结果：
1) 对比算法的计算效率。比较算法在计算过程中收敛于最优值的速度。
2) 对比最优值大小。通过10次求解最终目标函数值，比较梧州站削峰效果。
3) 对比每次求解结果的变异性。比较10次结果的标准方差和四分位范围。
GA与EDA10次计算平均每一代求解的最优个体适应度值结果如图4所示。
由图4中可以看出，经过10次计算的平均结果，除了EDA开始第一代计算所得到的平均最优适应度值比GA大，以后的进化中各代最优适应度值都比GA小。图中两条曲线在10代之前的都具有很大的斜率值，证明EDA和GA都能在前10代的进化计算中有很快的收敛速度，而之后的迭代中收敛速度变慢。在EDA求解的过程中，在第15代左右最优适应度值就可以收敛到最终优化结果，在此之后的几十代进化中每一代的最优适应度值变化不大，趋于稳定。而在GA求解过程中，在第40代左右最优适应度值才能接近最终优化结果。证明在计算效率的对比中，EDA比GA算法迭代速度更快，能够用更少的进化代数达到比较好的优化结果。
对比两种算法的梧州削峰效果，EDA最终求解的梧州洪峰流量为46,600 m3/s，使梧州100年一遇洪水量级降低到26年一遇，削减洪峰流量6100 m3/s，削峰率达11.6%；GA求解的梧州洪峰流量为46,830 m3/s，使梧州100年一遇洪水量级降低到28年一遇，削减洪峰流量5870 m3/s，削峰率达11.1%。EDA和GA都能够对梧州站的洪峰有很大的削减作用，而EDA可以比GA多削减230 m3/s。图5为10次计算最优结果的经验累积分布函
Figure 3. Wuzhou station discharge curve
图3. 梧州站流量过程图
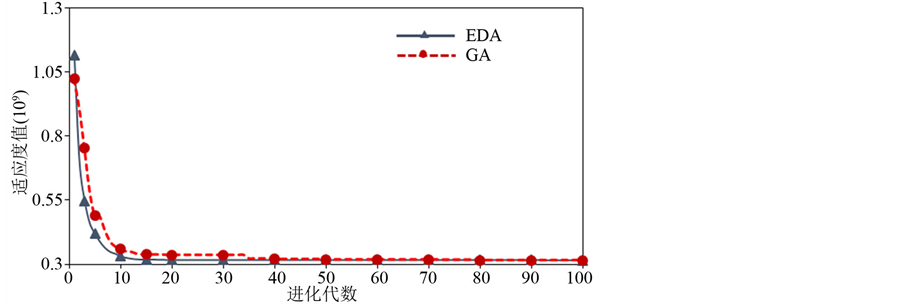
Figure 4. The average best values of the objective of each generation
图4. 每一代种群平均最优目标函数值
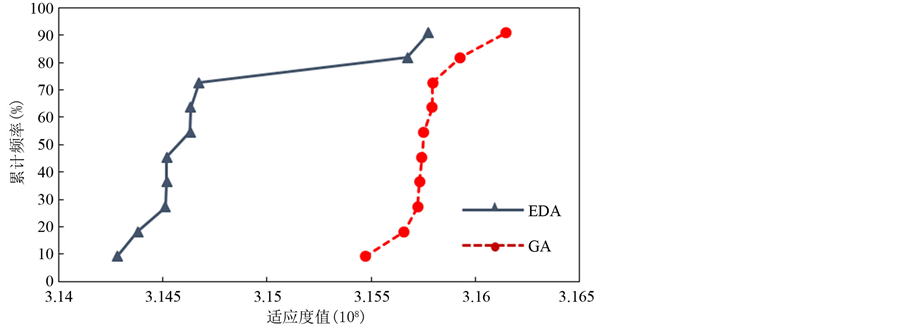
Figure 5. The empirical cumulative distribution function
图5. 经验累积分布函数
数图。由图5可知，EDA末代最优适应度值整体比GA结果要小，并且EDA有更大的概率获得较小的适应度值。
EDA10次计算得到的最优结果的标准方差为522,385.3，而GA10次计算得到的最优结果标准方差为174,108，EDA结果的标准方差大。图6是EDA和GA的最优结果四分位分布图，图中看出EDA的四分位范围比GA范围大。由标准差和箱状图结果可知，EDA求解的最优结果离散程度高，但即使最差的解，也与GA最优解相当。
5. 结论
本文建立了考虑马斯京根流量演算的短期水库群防洪优化调度模型，对短期优化调度中的滞时性进行了分析，介绍了遗传算法(GA)和分布估计算法(EDA)求解调度模型的步骤。以广西西江流域百色、龙滩并联水库群为例，以下游梧州防洪控制站最大洪峰流量最小为目标、一场百年一遇设计洪水过程为输入，利用GA与EDA对西江水库群调度模型进行求解。结果表明，EDA算法比GA算法有更快的速度收敛于最优值；EDA平均每次计算得到的适应度函数最优值比GA的结果更好、最优适应度得到较小值的概率更大；EDA比GA对下游梧州防洪控制站的削峰作用更明显。
基金项目
优秀青年科学基金(51422907)；水利部公益性行业科研专项经费项目(201201051)；中央分成水资源费项目(项目编号：1261430210028)。