1. 引言
非负矩阵分解[1] [2] (Nonnegative Matrix Factorization, NMF)是盲源信号[3] 分离主要理论工具之一,已引起学术界广泛关注和研究 [4] [5] 。为了保证分离唯一性和分离性能,需要在误差函数中添加各种约束条件 [6] - [9] ,如:行列式约束、稀疏性约束、正交性约束等。为保证分解矩阵的非负性,一般采用乘性更新规则。由于施加了多种约束条件,利用自然梯度下降法时,可以选择多种不同的学习速率,如何选择合适的学习速率,现有文献没有给出说明。对此本文进行了理论推导和大量实验研究,为基于NMF盲源分离算法的深入研究提供了理论基础。
2. NMF盲分离基本理论
令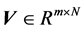 表示采样信号矩阵,
表示采样信号矩阵,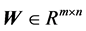 代表混合矩阵,
代表混合矩阵,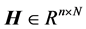 代表源信号矩阵,且
代表源信号矩阵,且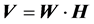 。盲源信号分离是指在源信号
。盲源信号分离是指在源信号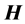 和混合过程
和混合过程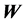 未知的情况下,从观察到的多个混合信号
未知的情况下,从观察到的多个混合信号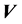 中重建出源信号
中重建出源信号 的方法。利用NMF进行盲源信号分离,就是要将
的方法。利用NMF进行盲源信号分离,就是要将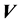 分解成两个矩阵
分解成两个矩阵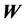 和
和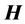 的乘积,并使分解误
的乘积,并使分解误
差尽可能小,采用2范数衡量NMF,其误差函数为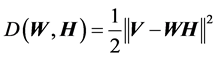 。为了提高盲源分离算法性
。为了提高盲源分离算法性
能,对误差函数施加行列式、稀疏性和正交性约束,设计NMF的优化目标函数如式(1)所示:
 (1)
(1)
其中, 、
、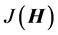 和
和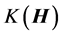 分别由式(2)、(3)和(4)给出;
分别由式(2)、(3)和(4)给出;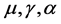 是平衡参数,为了保证NMF算法收敛,取比较小的正数。对于超定盲源分离,即
是平衡参数,为了保证NMF算法收敛,取比较小的正数。对于超定盲源分离,即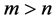 情况,有
情况,有
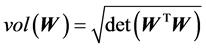 (2)
(2)
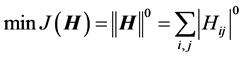 (3)
(3)
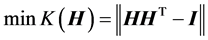 (4)
(4)
利用自然梯度下降法,求矩阵W和矩阵H的更新规则分别如式(5)和(6)所示。
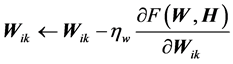 (5)
(5)
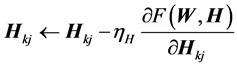 (6)
(6)
目标函数 对W和H的偏导分别如式(7)和(8)所示:
对W和H的偏导分别如式(7)和(8)所示:
 (7)
(7)
 (8)
(8)
3. 迭代更新公式
3.1. W迭代公式推导
由于非负矩阵分解要求得到的分解结果W和H是非负的,所以采用乘性迭代更新公式。为了得到W的乘性迭代更新公式,由式(7)可见,理论上可以选择三种不同的学习速率,从而应该有三种不同的W迭代更新公式。现以第一种学习速率选择为例,具体推导如下。
W的第一种学习速率可选择为
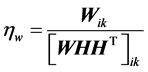 (9)
(9)
将式(7)代入式(5)右边,可得
 (10)
(10)
将式(12)代入上式可得
 (11)
(11)
因此可得关于W的第一种迭代更新公式为:
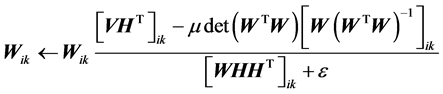 (12)
(12)
其中,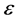 是一个很小的正数,是为了防止分母为零。下文其他处不再说明。
是一个很小的正数,是为了防止分母为零。下文其他处不再说明。
W的第二种学习速率可选择为
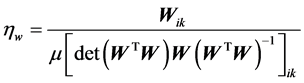 (13)
(13)
类似上述推导可得W的第二种迭代更新公式为:
 (14)
(14)
W的第三种学习速率可选择为
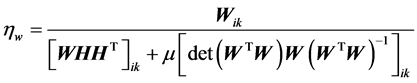 (15)
(15)
类似上述推导可得W的第三种迭代更新公式为:
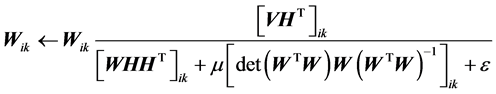 (16)
(16)
从式(12)、(14)和(16)可以发现,式(12)和(16)分母中包含有误差函数信息项 ,可以有效实现对W的更新。
,可以有效实现对W的更新。
3.2. H迭代公式推导
为了得到H的乘性迭代更新公式,由式(8)可见,理论上有7种不同的学习速率选择,从而应该有7种不同的H迭代更新公式。类似W迭代更新公式推导,分别可得7种不同的学习速率选择和H迭代更新公式如下。
H的第一种学习速率选择为:
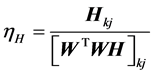 (17)
(17)
对应的H第一种乘性迭代更新公式为:
 (18)
(18)
H的第二种学习速率选择为:
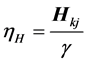 (19)
(19)
对应的H第二种乘性迭代更新公式为:
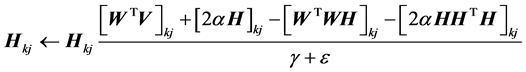 (20)
(20)
H的第三种学习速率选择为:
 (21)
(21)
对应的H的第三种乘性迭代更新公式为:
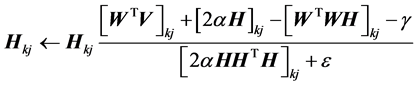 (22)
(22)
H的第四种学习速率选择为:
 (23)
(23)
对应的H的第四种乘性迭代更新公式为:
 (24)
(24)
H的第五种学习速率选择为:
 (25)
(25)
对应的H的第五种乘性迭代更新公式为:
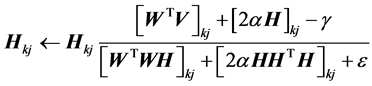 (26)
(26)
H的第六种学习速率选择为:
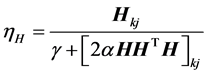 (27)
(27)
对应的H的第六种乘性迭代更新公式为:
 (28)
(28)
H的第七种学习速率选择为:
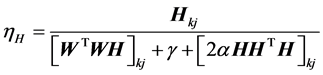 (29)
(29)
对应的H第七种乘性迭代更新公式为:
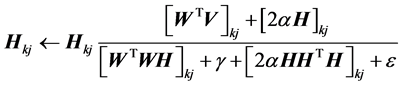 (30)
(30)
从上述迭代更新公式可以发现,只有式(18)、(24)、(26)和(30)含有误差函数信息项。所以W和H的乘性迭代更新公式可行组合形式如表1所示。
4. 算法仿真与性能分析
源信号图像如图1所示,随机产生非负混合矩阵,经过混合得到混合的图像信号。经过大量的仿真实验得到平衡参数的合适取值分别为: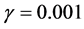 、
、 和
和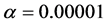 ,利用迭代公式更新W和H,迭代30,000次,更新迭代终止,最终得到由混合信号矩阵
,利用迭代公式更新W和H,迭代30,000次,更新迭代终止,最终得到由混合信号矩阵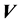 分离出的混合矩阵W和源信号H。
分离出的混合矩阵W和源信号H。
4.1. 迭代公式组合的有效性分析
大量的实验表明,分母中不包含有误差函数信息的迭代公式无法有效更新W和H,分离不出源信号,与我们前文判断一致。
现通过实验验证八种不同的迭代公式组合是否有效。应用上述八种迭代更新公式组合分离上述混合信号,算法能正常运行的用√表示,不能正常运行的用×表示,结果如表1所示。由表可见,即使八种组合分母中都包含了误差函数信息,但也只有三种组合方式是有效的,即组合3、组合4和组合7,所以可以得到三种算法,分别称为算法1、算法2和算法3。分析这三组迭代公式可见,迭代公式的分子分母项数基本平衡。
4.2. 三种算法性能分析
三种算法分离得到的图像信号分别如图2至图4所示。三种算法10次分离得到的源信号重构平均信噪比SNR如表2所示。由表2可见,算法2性能最好,算法1次之,算法3略差;三种算法性能在同一数量级,都能够较好地分离出源信号。

Table 1. Probability analysis of different iterative formulas
表1. 不同迭代公式组合的可行性分析
表2. 三种算法的重构平均信噪比(单位:dB)
5. 结束语
本文研究了学习速率选择对NMF的盲源分离算法性能影响。首先推导给出了选择不同学习速率时各种迭代更新公式,然后进行了大量计算机仿真实验,最后通过比较分析发现,有效的迭代更新公式的分母必须包含误差函数信息,分子分母的项数应尽可能平衡。
致谢
首先,我要感谢我的导
师赵知劲
教授。如果不是
赵
老师的悉心指导,无私地提出宝贵的修改意见,就不会呈现出这样一篇内容详实、推导严谨的论文。紧接着,我要感谢我的家人。在我专注于论文写作的过程中,是他们的鼓励与理解,让我得以全身心地投入我的写作,同时也激励着我去不断完善我的论文。最后,我要感谢所有帮助过我的老师和同学,这篇论文是大家共同智慧的结晶。再次感谢。