1. 引言
关于日月岁差与月球轨道交点西退的形成机制，至今仍是科学难题。根据宋晓东等的地球内核差异旋转研究成果，笔者提出“月球轨道运动改变地球各圈层角动量”的物理模型。由于地月系质心在地球内部，以及地球外核的液态特性，认为月球轨道运动会改变地球各圈层角动量，使地核远月半球的角动量与近月半球的角动量产生巨大落差。并形成地核(固态的内核和液体的外核)的差异旋转。由于地球的角动量守恒，会造成地幔壳的西移，形成日月岁差和春分点的西退。发现地球内核随月球的轨道运动在液核里游移，改变地球质心位置。当月球椭圆轨道运动进入近日、近地附近(即半通径位)时，月球的真近点角会由f = 270˚回(或前进)到f = 90˚。造成月球轨道交点西退及钱德勒极移。该发现对正确解释日月岁差和春分点西退形成机制有着重要意义，体会到我国先哲老子在《道德经》说：“大道至简，大音希声”及庄子的“天地有大美而不言，四时有明法而不议，万物有成理而不说”的深刻含义。
2. 我国学者的二项重要发现
“地球绕太阳公转一周，有恒星年和回归年之分。月球也类似于地球，在它绕地球的公转中，也有恒星月和朔望月之分。月球绕地球转360˚，叫做一个恒星月，这是月球公转的真正周期，等于27.3216日，它是以宇宙空间的恒星作为方向标志的。如果以月球的位相的变化周期来计算，例如从新月到新月，或从满月到满月的周期，叫做朔望月。朔望月的长度是29.5306日。”“月球绕地球运动的公转轨道面，即白道面。白道面和黄道面并不重合，而是有平均为5˚9'的交角，称黄白交角。这两个平面相交成一条直线，叫做交点线。交点线与天球有二个交点，……当从黄道以南经过交点运行到黄道以北，则此交点叫做升交点，另一个叫做降交点。”“交点有一个很重要的特点，就是交点在不断地移动(西退)，移动周期是18.6年，平均每年移动19˚21'。月球二次经过交点的时间是27.21222日，叫做交点月。”“月球绕地球运动的轨道是椭圆轨道，地球位于一个焦点上。月球连续二次经过近地点的时间间隔是一个近点月，近点月等于27.55455日。……月球轨道的近地点，也是不断移动。近地点的移动周期是8.85年。”[1]
中国地球物理学会天灾预测委员会陈国生先生为了预测地球灾害的需要，他深入研究月球的轨道运动。认为：“月球轨道(运行)周期长短是由地球轨道对月球近地点的位置决定的；从数学意义上看，月球轨道周期长短是由椭圆的偏心率决定的，也就是椭圆的焦点相对于圆(地)心移动变化所造成的。如图1
所示移动的范围在椭圆焦点O与O'或Q与Q'之间而且是左右对称。”(见图1)。陈先生说：“这里应注意：月球轨道的近地点出现在上、下弦位置附近时，近点月周期值缩短，只有24天多；近地点在朔望月位置附近时，近点月周期值延长，可达近29天，相差(最大时)将近5天。”他还发现：“月球在黄道上的投影曲线，每年的年末与年初是不重合的，如图2所示，每年超前90˚，4年超前360˚，月球位相复原。”[2] 河北省地震局研究员宋贯一在研究地球极移过程中发现：“在地球公转所处的四季位置中，自转极(北极)反向运动时间仅发生在当年的11月1日(立冬日为11月7、8日)到第二年的2月15日(立春日为2月4、5日)这一段时间之内；其它时间(季节)均为自转极正向(由西向东)运动时段。”[3] 为什么地球钱德勒极移自转极(北极)的正反向运动(极移)的时间不等？反向运动时间仅发生在当年的11月1日到第二年的2月15日这一时间段。
陈、宋二位先生的发现无疑是重要的。对日月岁差、月球轨道交点西退及钱德勒极移机制研究提供了研究方向。
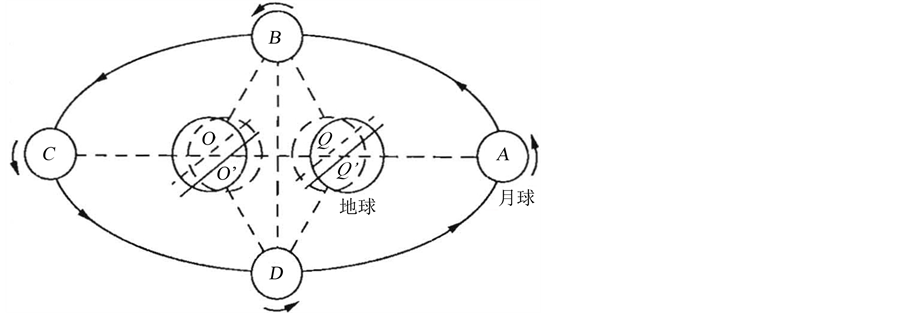
Figure 1. The length of the orbit of the moon
图1. 月球轨道周期长短示意图
Figure 2. Projection of the moon’s orbit in the zodiac
图2. 月亮运行轨迹在黄道上的投影示意图
3. “月球轨道运动改变地球各圈层角动量”物理模型
“宋晓东等在1996年发表的内核差异旋转研究成果，估计地球内核每年自西向东较外核多旋转1.1˚。自1990年到1996年累计已多转1/4圈多，引起国际学术界关注，并被评为1996年世界十大科技新闻之一。”“人们认识到，由于地核快轴对于内核自身而言，在短期内不应有明显的变化，……这种变化的起因应该是地核和整体地球之间，存在着旋转速度上的明显差异。因此只要能够把握内核快轴随时间的变化规律，就能确定内核相对于壳幔等其他固体圈层的差异旋转速率。”[4] 。根据宋晓东等的地球内核差异旋转研究成果，笔者提出“月球轨道运动改变地球各圈层角动量”的物理模型。对地球内核差异旋转的动力机制进行研究并“计算得出地球内核每年自转角速度增加0.000286˚”[5] 的结果。与宋晓东等在1996年发表的内核差异旋转研究成果估计地球内核每年自西向东较外核多旋转1.1˚相差很多。2012年8月中国教育和科研计算机网报道了《地核的旋转速度每数百万年增加1度》的文章。说：“科学家认为地核的旋转速度超过地球其他区域，每几百万年快1度。……指出他们已经第一次准确估算出地核与地球其他区域的旋转速度差异。地核的旋转速度实际上远远慢于此前的预计，大约每几百万年增加1度。”[6] 我们认为：尽管内核差异旋转的机制及具体增加度数还没有最后认定，但这一奇特发现对于认识地球深部动力过程，提供了极好的机会和手段，具有重要意义。
为什么地球内核的旋转速度超过地球其他区域？根据前人研究成果，我们提出了“月球轨道运动改变地球各圈层角动量”物理模型。图3为地球各圈层转动惯量示意图，O、O’、O”为地核、地月系、月球的质心。地球、地核(包括液体外核和固体内核)的质量和半径分别为：
，
，
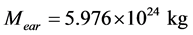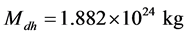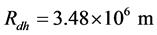
整体地球和地核(包括内核和液核)的转动惯量分别为：
；
；
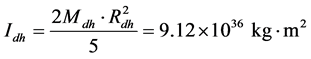则：地幔壳的角动量为：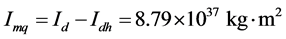
；
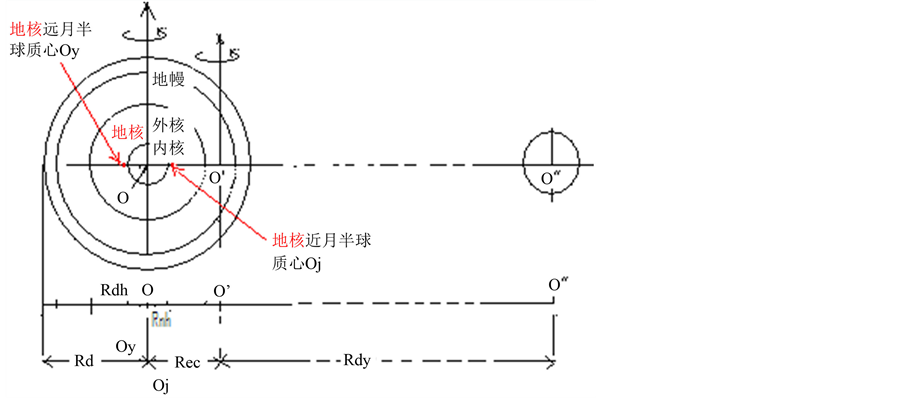
Figure 3. The moment of inertia of the earth, the earth's core and the earth’s inner core
图3. 地球、地核及地球内核的转动惯量示意图
地月系质心距地心的平均距离是：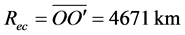
。月球在天球上循白道作椭圆运动，地核的
质心也会在液核中不断循白道面作小椭圆运动。考察地核绕地月质心运动过程中，分别以地心自转轴为界将地核分为近月半球和远月半球。据质心公式，球对称质量均匀分布半径为
的半球体，其质心位置
是：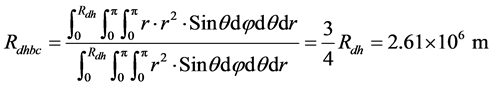
；得到地核的近月半球和远月半球的质心距地
球质心的距离是：
；则：远月半球的质心绕着地月系公共质心
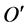自西向东运动的线速度为：
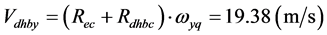；式中，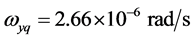
是地球和月球绕地月系质心
公转的角速度。近月半球的质心自西向东运动速度为：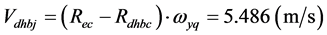
；(远月半球和近月半球质心的运动速度同向)。以地心为参考点，远月半球角动量与近月半球角动量之差是：
；
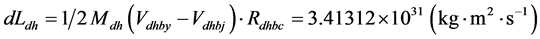地球自转的动力学方程是：
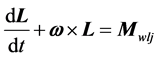
式中，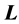
是角动量，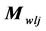
是受到的外力矩。如果地核远月半球角动量与近月半球角动量差异
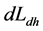不随时间变化，是不会引起任何力学效应。例如若地球是固体实心的，地核远月半球角动量与近月半球角动量差异
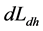不会随时间变化，是不会引起任何力学效应的。实际上地月系绕着太阳作轨道运动过程中，受太阳及行星的引潮力作用，“月球轨道的形状也是变化的，这反映在轨道椭圆的偏心率变化上，其值变化在1/15~1/23的范围内，平均值为0.0549。”[2] 当偏心率在平均值时，地月距离大致在
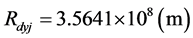至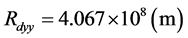
距离之间变化。说明地月系质心位置是在变动的。地月系质心位的计算公式是：
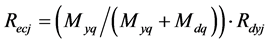；则：月球在近地点与远地点时，地月系质心距离地心的距离分别为：
；
；
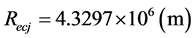因此，地核在月球的近地点时近月半球质心绕地月系质心运动的线速度为：
；
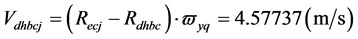在月球的远地点时远月半球质心绕地月系质心运动的线速度为：
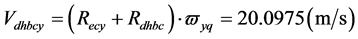
远月半球自西向东运动速度与地球自转同向，近月半球的自西向东运动速度与地球自转反向。由地球自转引起的在：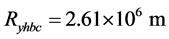
处的线速度是：
；式中，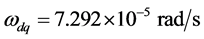
是地球自转角速率。它和由月球的轨道运动使地核远月半球和近月半球质心位置的线速度相加，则：远(近)月半球质心的转动线速度分别为：
；
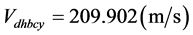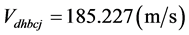
造成地核远、近月半球的角动量之差有：
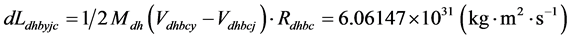
以地月系质心距地心的平均距离计算的造成地核远、近月半球的角动量之差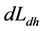
与随地、月轨道运动，以近地点到远地点计算的角动量差
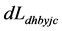比较，存在较大的差异。经计算有：
；
说明月球从近地点到远地点的轨道运动过程中，是月球轨道运动给地球的地核圈层增加了角动量。该角动量使地核(内核和液核)加快旋转，造成地轴晃动形成极移和章动。计算使地核(包括液核和内核)每周自转加快的大小是：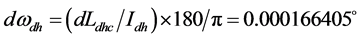
；因此说我们提出“月球轨道运动改变地球各圈层角动量”物理模型是能够解释地球各圈层的差异旋转，也可解释日月岁差及春分点西退，同时也可解释月球轨道升交点西移及钱德勒极移的激发机制。
4. 日月岁差和二分点西退的定量计算
由于地球各圈层角动量的改变是在月球的轨道运动过程中发生的，因此它是动态的、瞬变的，角动量是可以积累的。以2013年1月1日为例，查阅天文年历并计算，该日的地月距离有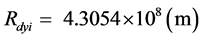
；根据质心计算公式：
；则：此位的地月系质心距离地心的距离为：
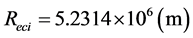；地核在该位的近月半球质心绕地月系质心运动的线速度为：
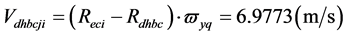；在远月半球质心绕地月系质心运动的线速度为：
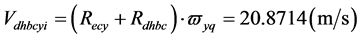远月半球自西向东运动速度与地球自转同向，近月半球的自西向东运动速度与地球自转反向。由地球自转引起的在：
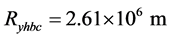；处的线速度是：
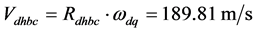；它和由月球的轨道运动使地核远月半球和近月半球质心位置的线速度相加，则：远(近)月半球质心的转动线速度分别为：
；
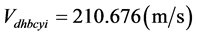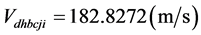；则2013年1月1日造成地核远、近月半球的角动量之差,也是该日地核的角动量增量有：
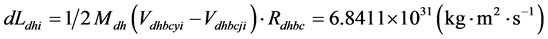
根据角动量守恒定律，假设地球液核与地球幔、壳的摩擦系数为零，则地球系统的地核角动量增大，则地球的幔、壳角动量会出现负值，即幔壳出现与地球自转反向的西向移动，则有：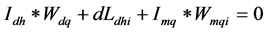
；即地球的幔、壳的动态角速度为：
；
由于地核的角动量是动态的，也是可以累加的，设年初的地核角动量增量初值(即1月1日初始值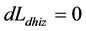
)为零，对一年的地核角动量增量进行累加，即
；
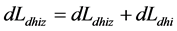我们应用Matlab软件，编制了模拟日地月三球的轨道运行程序，对一年中三球轨道运行过程中，地核的地幔壳的动态角动量的累计量进行计算，(见图4上)图中间红球为太阳、米字形为地球(米字形能观察地球的季节变化，黑粗线为黄道面以北的地球运行轨迹；绿色小球星号如(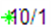
)为月球近地点时的大约时日)。并应用整体地球的角动量守恒定律计算地幔壳的动态角速度的累计量为：
；计算出地幔壳的一年中西向移动角度为：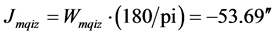
；(''/年)。(见图4下)。
而“春分点和秋分点向西移动，这一西移的平均速度是50.24''/年，叫做二分点的岁差。”[7] 与图4下：应用“月球轨道运动改变地球各圈层角动量”物理模型理论计算的一年西移角度相差：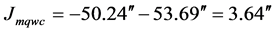
/年。分析造成上述情况的原因是由于地球外核的液态特性所造成。联想宋贯一的发现：“在地球公转所处的四季位置中，自转极(北极)反向运动时间仅发生在当年的11月1日到第二年的2月15日这一段时间之内；”结合图4下的地幔壳的一年累计转角(角秒)计算图显示。笔者认为：是地球液态外核的粘稠特性使地球各圈层一起，从年初至11月的地幔(壳)的正向转动。当月球椭圆轨道运动进入近日、近地附近时，很有可能有一种物理机制(受某种因素作用)，使地球自转极(北极)反向运动，使地核增加的角动量通过幔壳的西移而得到释放(好比角动量守恒原理使花样滑冰运动员张开双臂使自己停止旋转一样)，出现日月岁差和二分点的西退。同时也发生月球轨道交点西退及钱德勒极移，其激发机制需进一步研究。
Figure 4. The earth takes the moon around the sun (pictured above) and calculation chart of the accumulative rotation angle of the mantle crust for a year (pictured below)
图4. 地球带着月球绕太阳运行模拟图(上图)及地幔壳一年中西移累计转角计算图(下图)
5. 日月岁差及钱德勒极移形成机制研究
根据陈国生先生的发现：“月球轨道(运行)周期长短是由地球轨道对月球近地点的位置决定的；” “月球在黄道上的投影曲线，每年的年末与年初是不重合的，如图2所示，每年超前90˚，4年超前360˚，月球位相复原。”
根据宋贯一先生的发现：“在地球公转所处的四季位置中，自转极(北极)反向运动时间仅发生在当年的11月1日到第二年的2月15日这一段时间之内；其它时间(季节)均为自转极正向(由西向东)运动时段。”发现地球内核随地球和月球的轨道运动过程中，在太阳风及月球轨道运动改变地核角动量的共同作用下，会在液核里游移，改变地球质心位置。(见图1、月球轨道周期长短示意图)到了当年的11月5日左右，即在月球椭圆轨道运动进入近日、近地附近，月球的椭圆轨道运动到达约第12圈的半通径位相(上、下弦)时，因为该位：“即当真近点角f = 90˚或f = 270˚时的向径，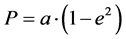
”[1] 的向径相等。加上地球外核的液态特性和地球角动量守恒的原因，会使地球自转极(北极)反向运动，(即相对地核的地球幔、壳西向运动)，使地核角动量迅速减小，大约于冬至日左右会自动归零，进入新的一年后月球轨道运动又会开始给地核不断增加角动量。
描述一年中日地月三球的轨道协同运动，在太阳风及月球轨道运动改变地核角动量的共同作用下，固体内核会在液核里游移，改变地球质心位置。同时月球的轨道运动不断给地核增加角动量加快液核的旋转，由于液核与月球相对应于地月系质心的公转角速度是相等的，所以月球轨道运动会出现“月球在黄道上的投影曲线，每年超前90˚……”的现象。当地月系再次进入近日、近地点附近时的冬至位置附近，月球公转轨道运动的真近点角会由f = 270˚回(或认为前进)到f = 90˚，出现宋贯一发现：“自转极(北极)反向运动时间仅发生在当年的11月1日到第二年的2月15日这一段时间之内；”的现象。(见图5、月球椭圆轨道运动真近点角由f = 270˚回到f = 90˚示意图)。实际上此时段可理解为月球椭圆轨道运动真近点角前进180˚，由f = 270˚前进到f = 90˚，期间的地核角量迅速减小，直至降至零位。进入新的一年后月
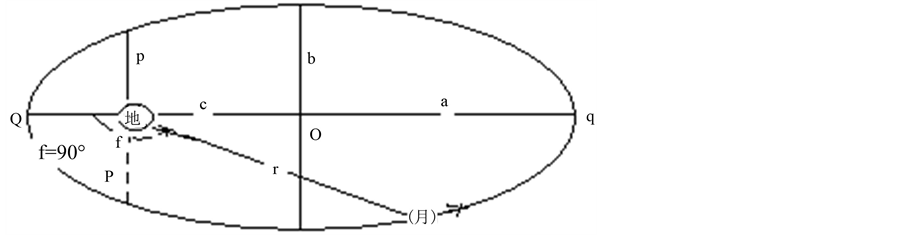
Figure 5. True near point of lunar elliptical orbit by f = 270˚ back to f = 90˚ 图5. 月球椭圆轨道运动真近点角由f = 270˚回到f = 90˚示意图
球轨道运动又会给地核增加角动量。月球轨道运动完全进入半通径f = 90˚位相时，月球轨道运动进入给地核增加角动量使地球的“自转极(北极)由反向运动……转为正向运动”的起始位。半通径f = 90˚位相是造成钱德勒极移的关键位。月球的轨道运动二次经过该位的周期时间就是钱德勒极移周期的时间，钱德勒极移周期就是这样形成的。自转极(北极)的反向运动反映地球遵循角动量守恒规律出现的地球幔、壳西向运动(相对于地核)，形成日月岁差和春分点西移，以及出现周年和钱德勒极移等现象。根据陈国生发现的“月球在黄道上的投影曲线，每年的年末与年初是不重合的，如图2所示，每年超前90˚，4年超前360˚，月球位相复原。”现象，笔者认为是太阳系日地月三球协同运动，月球的轨道运动不断给地核增加角动量加快液核的旋转，每年11月地球、月球运行到近日、近地点时，月球椭圆轨道运动真近点角会由f = 270˚回到f = 90˚地球在近日点作一次自身角动量的自动归零调整。因为每年超前90˚，二年超前180˚。因此出现地球自转速率的“二年准周期变化”[8] 。
6. 几点结论
(1) 地球带着月球绕太阳运行过程中，月球的轨道运动会改变地球各圈层角动量，使地核远月半球的角动量与近月半球的角动量存在巨大的落差，在形成地核的差异旋转的同时，也造成地轴的晃动及其极移。
(2) 月球的轨道运动造成的地核远(近)月半球的角动量差异，增加了地核的角动量。由于地球的角动量守恒，造成地幔壳的西移，形成日月岁差和二分点的西退。
(3) 发现当月球椭圆轨道运动进入近日、近地附近(即半通径位)时，地球椭圆轨道的真近点角会由f = 270˚回(前进)到f = 90˚，地球在近日点作一次自身角动量的自动归零调整。因为每年超前90˚，二年超前180˚。因此出现地球自转速率的“二年准周期变化”。认为地球的1.2年钱德勒极移的动力源来自月球，地球的年极移的动力源来自太阳。