1. 引言
全光纤电流互感器具有易于安装，抗电磁干扰，没有磁饱和效应，动态范围宽等优点。但是其在实用化过程中遇到了一对矛盾[1] ：一方面由于石英光纤的费尔德常数较低，为了提高灵敏度不得不增加光纤环的缠绕匝数；另一方面，光纤匝数的增加会额外的引入线性双折射，引入的线性双折射使得光纤电流互感器的灵敏度降低，过大的线性双折射甚至会抑制法拉第效应 [2] 。
本文从密勒矩阵着手，分析了偏振态在传感光纤中的演化过程，从理论角度分析了线性双折射值对输出偏振态的影响。同时发现，法拉第反射镜只有在电流为零时才能完全消除线性双折射，当电流不为零，不能完全消除线性双折射。从实验角度对理论进行了验证，实验还表明正交反射镜对振动有更好的免疫性。
2. 传输模型示意图
常用的全光纤电流传感器的传感头分为正交反射型和直接反射型 [3] - [5] ，其等效光路如下图。图1中采用的正交反射镜又称为法拉第反射镜，图2采用传统反射镜。
Figure 1. Transmission model of orthogonal reflector
图1. 正交反射式传输模型
Figure 2. Transmission model of direct reflector
图2. 直接反射式传输模型
密勒矩阵与琼斯矩阵类似，同样描述了光在通过光学元件后，输出偏振态与输入偏振态之间的变换关系。其与斯托克斯矢量结合，能在描述光的传输过程时给出更多的信息。
图1、图2中系统的等效密勒矩阵可以描述成：
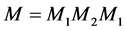(1)
上式中，
表示传感光纤对光偏振态变换的密勒矩阵，光正向传输与光反射后反向传输具相同的密勒矩阵；
是描述偏振光被反射式元器件反射时产生变换的密勒矩阵；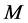
是描述偏振光在整个传输过程中的发生偏振态变换的等效矩阵。
传感光纤的密勒矩阵可以表述如下 [6] ：
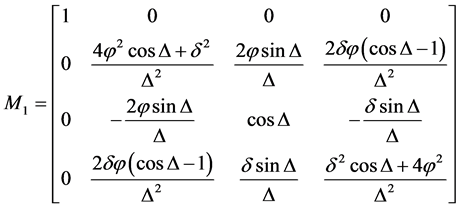(2)
式中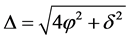
，
是由所有非理想条件引起的线性双折射的总和，包括光纤制造过程中产生的内在双折射和外部环境引起的外在双折射；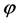
是由传感光纤中待测电流引起的法拉第转角，其计算公式为 [7] ：
(3)
式中V为Verdet常量，H为待测电流产生的磁场强度，当传感光纤在待测导体外部缠绕成环时，根据安排环路定理，上式又可以写成：
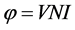(4)
N为光纤的环绕圈数，I为待测电流。
光路结构中的反射元件的密勒矩阵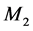
具有不同的形式，正交反射式结构中的法拉第反射镜的密勒矩阵 [6] ：
(5)
直接反射式结构中的传统反射镜的密勒矩阵 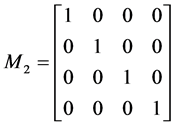[6] ：
(6)
2.1. 电流为零
电流为零时，法拉第转角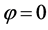
，根据式(2)传感光纤的密勒矩阵可以简化成：
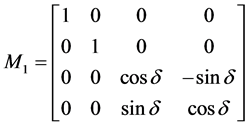(7)
根据式(1) (5) (7)，计算得到正交反射式结构的等效传输矩阵可以表示为：
(8)
根据式(1) (6) (7)，直接反射结构的传输矩阵为：
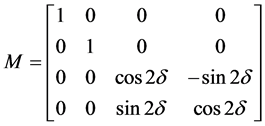(9)
比较式(7)~(9)可知，当电流为零时，正交反射式光路模型可以消除传感光纤中的线性双折射，而直接反射式的光路不能消除线性双折射，并且光路往返使双折射的效应加倍。由于线性双折射是互易 [8] 的，因此其大小与传输方向是无关的。对于正交反射镜来说，当光束正向传输到正交反射镜后，反射的同时，入射光的偏振面发生90˚旋转，使光矢的s分量与p分量交换方向，沿原路返回时产生的线性双折射与正向传输时产生的线性双折射恰好等值反向，因此在正交反射光路的等效传输矩阵中不含有线性双折射项，而对于直接反射式光路而言，反射时光矢的s分量与p分量没有发生交换，因此在反射时产生了与正向传输时等值同向的线性双折射，从而使得其等效矩阵中的双折射项为单根光纤中的两倍 [9] 。
2.2. 电流不为零
在电流不为零的情况下，同样得出正交反射式与直接反射式光路的等效传输矩阵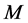
，令输入偏振光的斯托克斯矢量为
，那么，经过反射结构反射后输出光的斯托克斯矢量
可以表示成：
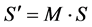(10)
根据输入光与输出光的斯托克斯矢量可以得到电流引起的偏振面旋转角度。
图3、图4反映了正交反射结构与直接反射式结构，在不同线性双折射下，其偏振面的旋转角度随电流值的变化情况。
从图中可以看出，当电流不为零的时候，正交反射镜和直接反射镜都不能消除线性双折射的影响，因为，如果假设反射式结构能够消除线性双折射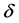
对系统的影响，那么偏振面旋转角度随电流的变化应该与
无关。图中
的值对曲线的形状有影响。所以两种反射镜均不能消除线性双折射的影响。
比较两幅图，还可以发现，在线性双折射为零时，正交反射式光路与直接反射式光路其光束偏振面的转动角度随电流的变化是相同的，并且表现出很好的线性；当线性双折射小于
时，低电流时曲线的斜率要整体高于右图，线性双折射对正反射系统的影响要小于直接反射系统，或者可以理解为正交反射系统部分消除了线性双折射的影响 [10] 。在正交反射式系统中，偏转角度随电流的变化仍然有较强的线性，仅是曲线的斜率变小，而在直接反射式系统中，曲线不再呈线性变化，并且严重偏离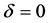
时的曲线。
实验验证了上述的结论，同时还发现，法拉第反射式结构相比与直接反射式结构具有更强的振动免疫性。
Figure 3. Orthogonal reflector: rotation of polarized plane with different current
图3. 正交反射镜：偏振面旋转随电流值变化
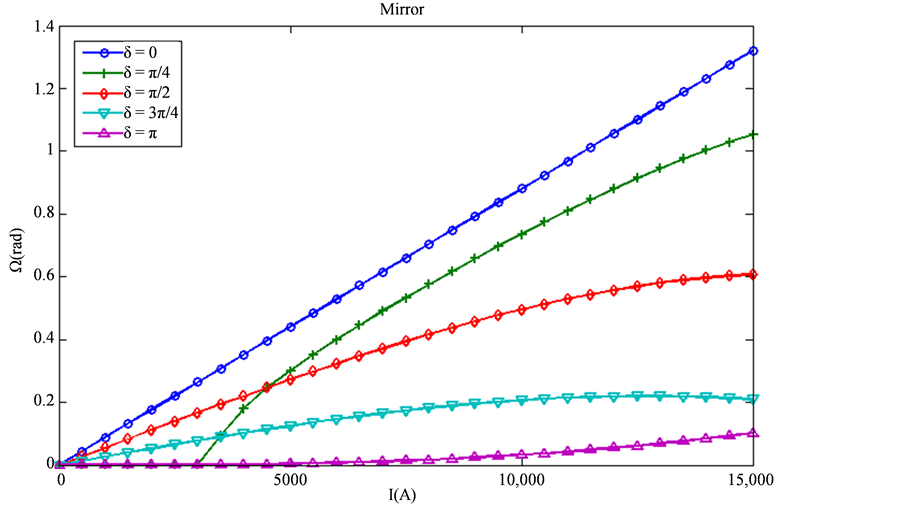
Figure 4. Direct reflector: rotation of polarized plane with different current
图4. 直接反射镜：偏振面旋转随电流值变化
3. 实验
3.1. 实验光路(见图5)
反射器反射后的偏振光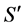
经过环形器后从主光路分离，在偏振分束器中分成两束振动方向相互垂直的正交光，分别由两个光电探测器接收其光强
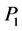及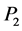
并转换成电信号 [11] ，经电子运算器得到
：
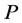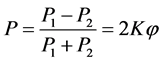(11)
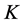是与光纤性能及光电转换有关的系数。
3.2. 线性双折射对不同反射结构的影响
实验中分别采用普通单模光纤和LB低双折射光纤作为传感光纤，反射元件分别采用正交反射镜和直接反射镜，通过两两组合，来阐述线性双折射对系统的影响。虽然无法定量测出以上传感光纤与反射元件组合后系统内的双折射大小，但是通过传输矩阵的理论分析可以得出线性双折射从小到大的顺序分别为：1) 低双折射光纤与法拉第反射镜(LBF + FRM)；2) 单模光纤与法拉第反射镜(SMF + FRM)；3) 低双折射光纤与普通反射镜(LBF + Mirror)；4) 单模光纤与普通反射镜(SMF + Mirror)。因为正交反射镜可以部分消除光纤内部的线性双折射，而传统反射镜的效果会使光纤内的线性双折射加倍 [12] 。所以采用法拉第反射镜的实验组，其系统内部的双折射要整体小于采用传统反射镜的实验组；低双折射光纤的线性双折射要小于普通单模光纤，所以反射镜相同时，采用低双折射光纤的系统内的双折射要小于采用单模光纤的实验组。
分别作出四组实验的拟合曲线如图6、图7，图中纵坐标M表示输出信号上式(11)中输出信号
的均方根峰值。图6中数据点的线性强于较图7，图7中数据点在电流较大时偏离拟合曲线且向下弯曲。比较两幅图可以发现，采用相同反射元件，单模光纤做传感光纤时数据点拟合的斜率总是要小于低双折射光纤。而图6中两条拟合曲线的斜率整体大于图7。这也验证了线性双折射越大，曲线斜率越低的结论。
Figure 6. Faraday Mirror: M values changes with different current
图6. 法拉第反射镜：输出值随电流值变化
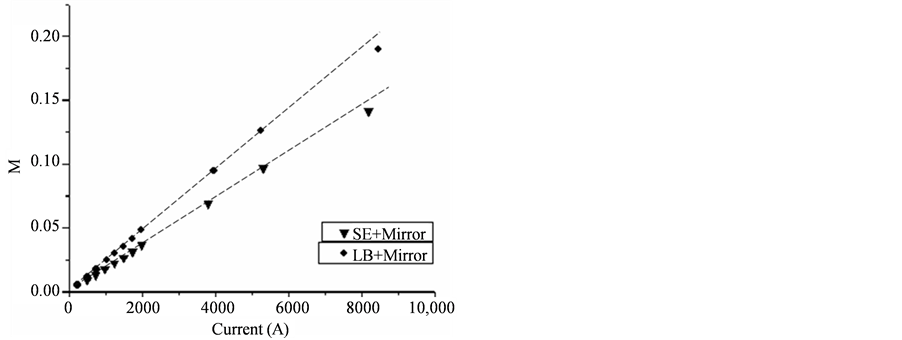
Figure 7. Mirror: M values changes with different current
图7. 直接反射镜：输出值随电流变化
3.3. 振动对不同反射结构的影响
实验采用50 Hz交流电，待测电流值为1000 A，LB作传感光纤，比较不同反射结构对外界振动的免疫性用重物敲击传感光纤环来模拟外界振动。输出信号的波形如图8中(a)、(b)，可以看出，当采用正交反射镜时，在外界振动突然来到时，波形基本不发生变化；采用传统反射镜时，波形完全变形；振动消失，波形也随之恢复。
由于法拉第反射镜可以通过交换正交的偏振态部分消除双折射，所以当振动引起光纤内部双折射变化时，FRM反射镜可以一定程度上减小这种变化 [13] ；但是对反射镜而言，这种变化是双倍的，当信号淹没在振动引起的线性双折射中，波形就会发生紊乱 [14] 。
3.4. 温度稳定性测试
温度变化时，由温度产生的热应力也会导致光纤内部的线性双折射变化，从而影响测量精度。实验中，反射结构均采用正交反射镜，传感光纤分别采用低双折射光纤和单模光纤 [15] ，系统输出值M随时间变化的曲线。图9、图10中为传感光纤为LB光纤，在十分钟内，当温度从20℃均匀上升到70℃时，可以看出输出值有明显的下降，说明在温度上升时，LB光纤内部的线性双折射也随之升高。而单模光纤却呈现缓慢上升趋势，这说明在温度上升时，单模光纤内部的线性双折射反而减小，但这种趋势不明显且在8分钟左右时逐渐变得平缓。
造成这两种不同趋势的一种可能的解释是 [14] ：实验中采用的低双折射光纤在制造过程中，预制棒在拉纤的同时，绕轴自转。当温度上升时，拉纤过程中旋转产生的应力得以释放，从而影响了光纤的性能，同时由于光纤涂覆层与外部松管套在受热过程中具有不同的伸缩系数，伸缩系数不匹配产生的应力也会对光纤的传感性能产生影响，但对单模光纤而言，这种应力恰好在某种程度上补偿了线性双折射的影响，从而使得曲线呈现缓慢上升的趋势，这是采用预偏置角补偿来补偿线性双折射从而补偿温度变化的原因 [16] 。
4. 总结
文章从密勒矩阵出发，推导出光纤电流传感器中正交反射式结构及直接反射式结构的等效传输矩阵，证明当电流为零时，正交反射式结构能够消除线性双折射的影响。在电流不为零时，通过传输矩阵，给出了偏振面旋转随电流变化的曲线，曲线表明：相同的线性双折射对正交反射式系统的影响要明显小于
(a) (b)
Figure 8. Output in vibration of signal with different reflectors. (a) Orthogonal reflector: output in vibration of signal; (b) direct reflector: output in vibration of signal
图8. 外界振动对输出信号的影响。(a)振动对正交反射系统的影响；(b)振动对反射系统的影响
Figure 9. Temperature stability of low birefringence fiber
图9. 低双折射光纤的温度稳定性
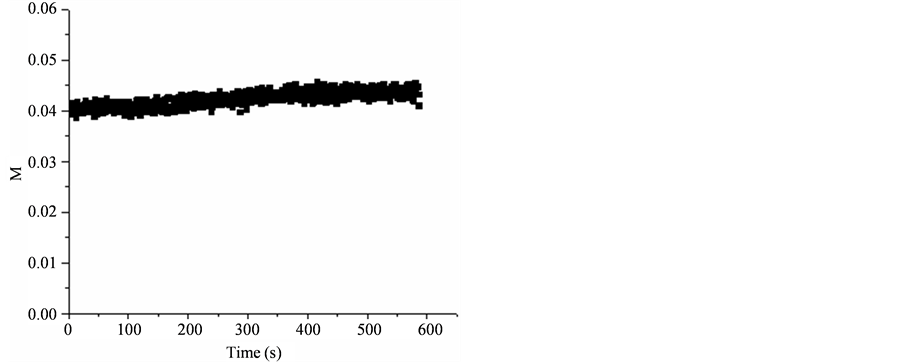
Figure 10. Temperature stability of single mode fiber
图10. 单模光纤的温度稳定性
直接反射式系统。在随后的实验同时还表明：正交反射式结构相比直接反射结构有更好振动免疫性。所以采用正交反射镜时，基于偏振检测类型的光纤电流传感器具有更好的性能。对不同光纤的温度稳定性进行了分析，给出了一种温度补偿的方案。
致谢
感谢广东省部产学研项目提供资金支持，感谢深圳太辰光通信股份有限公司的大力合作。
基金项目
受广东省省部产学研项目(2012B091100096)资助。