1. 引言
随着便携式摄像设备手机、计算机等大规模使用和多媒体技术的快速发展,人们正接触着越来越多的图像信息,如何快速高效地从海量图像中获取用户所需要图像成为当前研究的热点。基于内容的图像检索(CBIR)因此应运而生。近年来,基于内容的图像检索技术在商业方面得到了较大的应用,如百度的百度识图、安图搜的购物搜索引擎、淘宝的拍立淘、数之联的拍图购等。
第三代人工神经网络脉冲耦合神经网络(PCNN)无需提前训练样本,从生物视觉出发处理图像更符合人类的视觉机制,用于图像检索时具有旋转、缩放、平移不变性的特性[1] ,使得PCNN广泛应用于图像分割、边缘检测、图像去噪、图像融合、特征提取等领域[2] 。文献[3] 利用PCNN生成的时间序列作为特征对纹理图像进行检索。文献[4] 利用PCNN提取图像边缘信息,生成边缘时间序列作为图像特征用于商标检索。文献[5] 计算PCNN生成二值图像的欧拉数,将欧拉数序列作为图像特征用于图像检索。由于PCNN参数设置较多,参数取值需要人工确定,一定程度上限制了其应用。为优化PCNN参数,Deng X Y等[7] 从PCNN数学特性出发,对其点火机理进行分析,提出了改进模型用于图像分割。Zhou D等[7] 利用脉冲输出所对应区域均值和阈值的关系,对PCNN模型的连接系数进行优化,将改进后的模型用于图像分割。但以上参数优化方法都需要结合图像的自身信息,不同图像得到不同的优化参数,不适用于图像检索。文献[8] [9] 引入遗传算法对PCNN参数进行优化。但该方法需要对参数进行编码,且算法中包含复制、交叉、变异等操作,实现相对复杂。Kennedy等人[10] 提出的群智能粒子群算法,具有原理简单,收敛速度快,参数设置少,易于实现等优点,因此本文引入粒子群算法用于优化PCNN参数,并将优化参数的PCNN用于图像检索。
2. 脉冲耦合神经网络
数脉冲耦合神经网络是Echorn等人受猫的视觉皮层神经信号传导特性启发,并由Johnson等人改进为适用于图像处理的新型神经网络。其数学表达式如下:


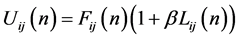


式中F、L为PCNN的反馈输入和连接输入。U为内部活动项,Y为脉冲输出,θ为动态阈值。 、
、 为神经网络中各神经元坐标,
为神经网络中各神经元坐标,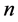 为PCNN迭代次数。
为PCNN迭代次数。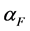 、
、 、
、 分别为时间衰减系数,
分别为时间衰减系数,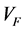 、
、 、
、 分别为幅度系数,
分别为幅度系数,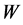 、
、 为连接矩阵,
为连接矩阵, 为连接系数。在图像处理中,反馈输入为图像本身S,图像中各像素点代表神经网络的各神经元,某一神经元的点火会触发周边相似神经元点火,因此一次迭代后所有神经元输出形成的二值图像包含原图像的纹理、边缘等信息,可作为图像特征并应用于图像检索。
为连接系数。在图像处理中,反馈输入为图像本身S,图像中各像素点代表神经网络的各神经元,某一神经元的点火会触发周边相似神经元点火,因此一次迭代后所有神经元输出形成的二值图像包含原图像的纹理、边缘等信息,可作为图像特征并应用于图像检索。
3. 基于粒子群算法的参数优化
3.1. 粒子群算法
粒子群算法是受鸟类寻找食物启发而用于求解优化问题,通过评价函数确定各粒子位置的优劣,各粒子的位置由其速度所定,其优化过程中各粒子主要依靠历史最佳位置和全局最佳位置进行速度更新、确定新位置,进而通过评价函数找到其最优位置。达到终止条件时,找到最后的全局最佳位置为其最优解[11] 。其具体描述为在D维搜索空间,粒子群数量规模为n,粒子的位置为 ,速度为
,速度为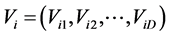 ,各粒子的历史最佳位置为
,各粒子的历史最佳位置为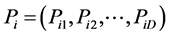 全局最佳位置为
全局最佳位置为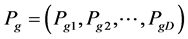 ,
, 为
为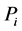 中的最优值。其中
中的最优值。其中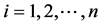 。各粒子位置和速度更新公式如下:
。各粒子位置和速度更新公式如下:


式中 为迭代次数,
为迭代次数,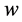 为惯性因子,
为惯性因子, 、
、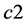 为学习因子,rand( )为取值为[0, 1]之间的随机数。惯性因子和
为学习因子,rand( )为取值为[0, 1]之间的随机数。惯性因子和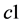 越大,其全局搜索能力越强,
越大,其全局搜索能力越强, 越大,其局部搜索能力越强。为避免算法过早进入局部最优,本文采用文献[12] 方法,在算法运行前期给
越大,其局部搜索能力越强。为避免算法过早进入局部最优,本文采用文献[12] 方法,在算法运行前期给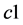 赋较大权重系数,后期将
赋较大权重系数,后期将 权值动态调整增加,减小
权值动态调整增加,减小 权值。其动态调整公式为:
权值。其动态调整公式为:


其中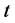 为迭代次数,
为迭代次数, 为算法的总迭代次数,随着迭代次数增加,
为算法的总迭代次数,随着迭代次数增加, 由大变小,
由大变小, 由小增大,动态增强了粒子群算法跳出局部最优的能力。
由小增大,动态增强了粒子群算法跳出局部最优的能力。
3.2. 基于粒子群算法的参数优化
PCNN中需要优化的参数主要有5个,分别是 ,
, ,
, ,
,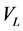 ,
, 。将5个待优化参数作为粒子的维度输入到粒子群算法中。为确定粒子群算法的评价函数,本文采用时间熵序列[13] 作为图像的PCNN输出,其中二值图像的香农熵定义为:
。将5个待优化参数作为粒子的维度输入到粒子群算法中。为确定粒子群算法的评价函数,本文采用时间熵序列[13] 作为图像的PCNN输出,其中二值图像的香农熵定义为:

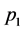 、
、 分别为二值图像中1和0出现的概率。
分别为二值图像中1和0出现的概率。
本文计算图像时间熵序列之间的相关系数,以判断图像的相似程度,相关系数越大,图像间的相似度越高。相关系数算法公式为:
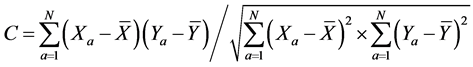
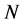 为PCNN的迭代次数,本文设置
为PCNN的迭代次数,本文设置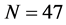 。
。 、
、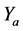 为图像X和图像Y在第
为图像X和图像Y在第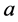 次迭代时的香农熵,
次迭代时的香农熵,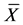 、
、 为图像X和图像Y在
为图像X和图像Y在 次迭代后的香农熵平均值。
次迭代后的香农熵平均值。
为寻求优化参数,选用 幅图像作为训练图像,即共有
幅图像作为训练图像,即共有 类图像,每类中
类图像,每类中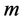 幅。其优化过程为:
幅。其优化过程为:
(1) 把粒子的维度作为PCNN参数,用PCNN计算训练图像的时间熵序列;
(2) 计算所有训练图像时间熵序列间的相关系数;
(3) 找出 类图像中最小的相关系数值
类图像中最小的相关系数值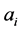 ;
;
(4) 找出 类图像与非
类图像与非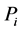 类图像间最大的相关系数值
类图像间最大的相关系数值 ;
;
(5) 对图像每类 重复步骤3和4 (
重复步骤3和4 ( );
);
(6) 找出a中的最小值与b中的最大值,并计算它们的差值,作为粒子的适应值,差值越大效果越好;
(7) 对每个粒子重复1~6步,计算每个粒子的适应值;
(8) 根据适应值确定粒子全局最佳位置和历史最佳位置,进行更新迭代。
算法中的主要参数设定,粒子规模为20,迭代次数10次,惯性因子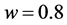 。训练图像共选取2类,每类5幅,所有图像来自于corel图像库。
。训练图像共选取2类,每类5幅,所有图像来自于corel图像库。
3.3. 参数优化的PCNN图像检索
Ma Y等[14] 证明了在参数适当的情况下,每幅图像经PCNN处理后都有唯一图像特征,因此可以将PCNN处理后的图像序列作为图像的特征用于图像检索。由于经PCNN处理后每次迭代都产生一幅二值图像,生成的图像数据较多,不利于后续处理。为减少数据量,Johnson [15] 等人提出时间序列,即统计迭代中每幅二值图像的非零值求和,经过N次迭代得到含有N个元素的一维向量,即为图像的时间序列。时间序列极大地减少了数据量,但其抗干扰能力较差。本文采用时间熵序列作为图像特征。对图像库进行PCNN操作,生成时间熵序列库作为图像特征库。
常用的相似性度量方法有欧氏距离法、马氏距离法、积相关法、相位相关法和相关系数法等,因相关系数法具有几何不变性和较好的抗噪能力[16] ,本文采用相关系数来度量图像时间序列熵间的相似度,进而求得相似图像。
4. 实验结果及分析
本文实验环境为Microsoft Windows 7、Intel(R) Core(TM)i5-3470 cpu@3.2 GHz、3.2GHz、8.0 GB内存、MatlabR2008a。实验选用corel1000图像库中图像。分别从花朵、恐龙两类图像中选出5幅作为粒子群算法的训练图像。实验前先将彩色图像转制为灰度图像。
为检测优化后参数的效果,首先对训练图像进行测试,随机选取5张图像作为查询图像,返回排行靠前的前5幅作为查询结果,取查询结果的平均值作为图像的查准率和查全率。图1为检索结果。由图1可以看出经粒子群算法优化后的PCNN在查准率和查全率上均取得较好效果。
将优化后参数与文献[3] 中采用的经验参数对比,经验参数取值如表1所示。
连接矩阵W为 矩阵,各元素取值为各元素自身与矩阵中心距离的倒数,具体形式为:
矩阵,各元素取值为各元素自身与矩阵中心距离的倒数,具体形式为: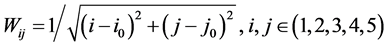 ,
, 、
、 为
为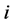 、
、 的中心。
的中心。
图像库采用corel1000图像库中的花和恐龙两类图像共200幅。图2为对corel1000图像库中第606幅花朵图像的检索结果对比,从主观上看,本文设计方法的检索结果更符合人类视觉,检索结果与查询
图像有更高的相似性。
从每类图像中随机选取5幅作为查询图像,分别选用两组PCNN参数进行检索比较。其检索结果如图3、图4所示。
从图3、图4可以看出,经本文优化后的参数用于图像检索时在查准率和查全率上都明显优于经验参数。实验中选用了10幅图像为训练图像,用其它未训练图像进行查询时,本文的优化参数仍表现出较好的检索效果。

Figure 1. Average precision ratio and recall ratio
图1. 平均查准查全率曲线
表1. PCNN的基本参数

Figure 2. Comparison of single image retrieval results
图2. 单幅图像检索结果比较

Figure 3. Precision ratio comparison between two methods
图3. 查准率比较
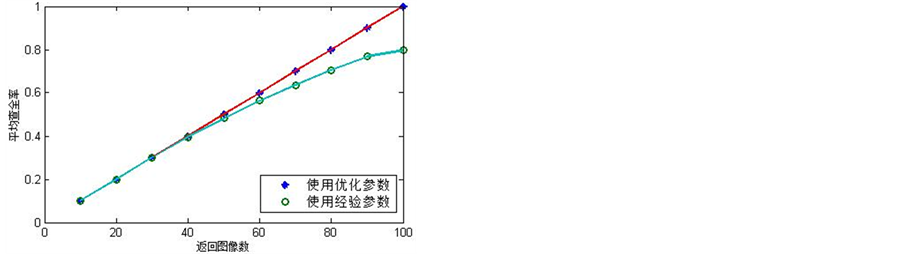
Figure 4. Recall ratio comparison between two methods
图4. 查全率比较
5. 结论
针对PCNN参数较多且依靠经验取值严重影响检索效果的问题,本文提出构建评价函数,利用粒子群算法对PCNN参数进行自动寻优,将优化后的PCNN参数用于图像检索。结果显示,该方法效果较好,具有较高的查准率和查全率。利用粒子群算法训练时只需要少量图像即可,训练开销相对较小。对未训练图像进行检索时也能取得较好结果,且检索结果更符合人类视觉。