基于农作物生长优选环境的方差分析模型

The ANOVA Based on Crop Growth Optimization Environment

摘要: 物联网在农业中的应用，使一系列作物在不同生长周期被模糊处理的问题，都得到了良好把关。然而这种精确把关，从某种程度上讲也是远程控制技术人员经验，感觉的反映。本文基于农作物生长优选环境的选择，对面向农业物联网监测到的数据，采用统计中的方差分析方法构建模型，将统计方法与农业问题的解决相结合，进而准确定量的寻找作物生长的最佳试验点，保证农作物有一个良好适宜的生长环境，并试图将这种方法应用于实践中。

Abstract: The application of the Internet of things in agriculture has made a series of crops problems in dif-ferent growth periods be well controlled. However, the precise control, to some extent, is also the reflection of experience and feeling from technicists who take charge in the remote control tech-nology. This article based on the choice of crops growth optimizing environment, monitoring date from the agriculture network and construction of model by statistical method of ANOVA, combines statistical method with agriculture problem in order to accurately and quantificationally discover the best sites for crop growth and ensure that crops have a suitable growth environment and even-tually put this method into practice.

1. 引言

物联网被世界公认为是继计算机，互联网与移动网之后的世界信息产业第三次浪潮。与传统的农业相比，浇水，施肥，打药全凭经验，靠感觉，而农业物联网技术的应用，瓜果蔬菜该不该浇水？施肥，打药怎样保持精确的浓度？温度，湿度如何实现按需分配？农民只需按个开关，做个选择，或是完全听“指令”，就可以种好菜，养好花。然而农业物联网的这种“精确”把关，从某种程度上讲，也是远程控制技术人员经验，感觉的反映[1] 。

多元统计分析中的方差分析模型是20世纪发展起来的一种统计方法，它是由英国统计学家进行试验设计时为解释试验数据而首先引入的 [2] 。目前，方差分析广泛应用于分析心理学，生物学以及工程和医药等的试验数据中。方差分析形式上是比较多个总体均值是否相等，本质上是从数据误差来源的分析入手，分析分类自变量对数值因变量的影响，寻找最佳试验点或控制变量的最优组合。本文基于农作物生长优选环境的选择，对面向农业物联网监测到的数据，采用统计中的方差分析方法构建模型，从而试图定量的解决作物生长过程一系列被模糊处理的问题，并进一步研究提高农作物产量的最优组合生长环境。

2. 试验设计

在一次基于物联网监测数据的农业试验中，研究影响玉米产量的因子，试验中选用了三个玉米品种，分别施用三种肥料，然后在面积和肥沃程度基本相同的土地上进行试验。试验结果见表1。在误差允许的范围内，控制其它生长环境几乎理想的情况下，采用交互分组和二种因素配合进行试验 [3] 。一般而言，在农业生产中，玉米的产量越高，说明生长条件越适宜，但这种高产量究竟是因为条件适宜产生的，还是偶然因素造成的，实际中我们经常模糊处理，而本文我们将从统计的角度进行定量的分析。寻找作物

Table 1. Corn variable under different experimental conditions

表1. 不同试验条件下的玉米产量

生长的优选环境即分析影响作物生长的不同因素组合下的产量是否有显著差异，实际上是判断不同的因素组合对农作物的产量是否有显著影响，做出这种判断最终被解释为从误差来源分析入手，寻找造成作物产量的这种差异来源于何种原因。基于北京农业信息技术研究中心监测到的数据统计结果如上，采用简单随机抽样保证了样本的独立性，对数据采用EXCEL进行双机录入保证了数据的准确性，并基于SPSS20.0进行数据的建模分析。

3. 构建数学模型

3.1. 问题分析，确定观测变量和控制变量

研究中物联网监测到的可测指标为玉米产量，涉及的可控因素有两个，分别为品种和肥料。可控因素各有3个水平，每个水平可以看作一个总体，监测到的数据可以看做从相应总体中抽取的样本。从数据的结构可以看到，每两个因素的交叉处进行了重复试验，因此我们可以设法构建平衡态下有交互作用的双因素方差分析统计模型。假设行控制变量有k个水平，列控制变量有r个水平，每个交叉水平处有p个样本，则在行控制变量的第i个水平和列控制变量的第j个水平下的第m个观测值可表示为

，；；

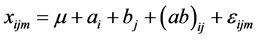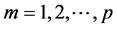
其中为抽样误差，是服从正态分布的独立随机变量，为行因素的效应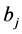，为列因素的效应，为二者的交互效应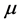，为总均值。

3.2. 剖析观测变量的方差，确定离差分解式

基于统计的方法来处理农业问题本质上是将统计中的数据处理思想应用于农业生产问题的研究中，方差分析的思想是分析数据的误差来源。交叉处进行了重复试验，则试验数据中的总差异中应包含有各个可控因素所引起的独立主效应和随机因素所引起的变异，以及通过各个水平间搭配对试验结果产生交互影响（即各可控因素交互作用所引起的变异）。故研究中我们应考虑品种，肥料这两个可控因素引起的以及随机因素的变异和两个可控因素的交互作用引起的变异 [4] 。这样我们采用统计中误差的完全离差分解方式，则完全离差分解式：

3.3. 提出统计假设

根据上述的分析我们做出如下的统计假设：

原假设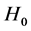：肥料对玉米产量无显著影响；品种对玉米产量无显著影响；

肥料和品种的交互作用对玉米产量无显著影响。

3.4. 进行离差分析，将条件误差，交互作用，与随机误差进行比较，得方差分析表

若为对应于行因素的第i个水平和列因素的第j个水平的第m个观测值；

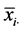为行因素的第i个水平的样本均值；

为列因素的第j个水平的样本均值；

为行因素的第i个水平和列因素的第j个水平的样本均值；

为全部n个观测值的总均值。

则总的离差平方和：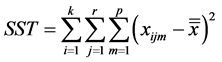

行因素离差平方和：

列因素离差平方和：

交互作用离差平方和：

误差平方和：

为了检验行因素的主效应是否显著，构建F检验统计量为：

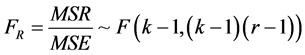
为了检验列因素的主效应是否显著，构建F检验统计量为：

结果见表2，表3：

基于SPSS20.0进行统计分析，可以得到玉米产量的双因素方差分析结果为

Table 2. Data structure of double factor variance analysis in equilibrium state

表2. 平衡态下双因素方差分析数据结构

Table 3. Test of the effect of the subject

表3. 主体间效应的检验

^aR方 = 0.842 (调整R方 = 0.807)

3.5. 统计决策

对于给定的显著性水平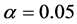，从检验的结果可以看到，肥料和品种各自独立主效应的相伴概率p分别为0.000和0.000，均小于给定的显著性水平，说明选取不同的肥料和品种对玉米的产量具有显著的影响，在作物的生长过程中应加以重视，而二者的交互效应的相伴概率p为0.990，远大于给定的显著性水平，故不能说明二者的交互效应在统计上对玉米产量有显著影响。调整的R方反映模型对观测数据的总体拟合程度，越接近1说明拟合程度越高。该模型调整R方 = 0.807，说明拟合的还比较理想，从另一个角度说明玉米产量主要受行列主效应的影响 [5] 。

3.6. 关系强度的测量

在上面的数据模型分析过程中，行平方和度量了肥料对玉米产量的影响效应，列平方和度量了品种对玉米产量的影响效应，而二个平方和加在一起共同度量了主效应对玉米产量的联合效应，联合效应与

总平方和的比定义为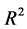，其平方根反映了主效应与因变量之间的关系强度。即，

两个主效应解释了玉米产量差异的84.05%，其它因素（交互效应和残差效应）只解释了15.94%，说明肥料和品种的不同与玉米产量之间有较强的关系 [6] 。

4. 结果分析

4.1. 控制变量交互作用的图形分析

分析发现品种和肥料的交互效应没有对玉米的产量产生影响，为了直观的显示该结论，我们进行交互作用的图形分析，结果见图1。

在品种从水平1变化到水平3的过程中，肥料3个水平下的玉米产量基本按照相同的规律变动，各直线在各个水平基本平行，所以品种和肥料之间对玉米的产量无明显的交互影响，和我们数据拟合的结果是一致的 [7] 。

4.2. 均值检验

基于品种多重比较(表4)和偏差对比(表5)以及箱线图2的结果，可以看到品种1和2，3之间对玉米的产量有显著性的影响效应，且品种1作用下的玉米产量均值最大，总体产量都比较高，是我们重点关注和考察的品种 [8] 。

而对肥料的多重比较(表6)以及K矩阵偏差对比(表7)和箱线图3的结果表明，肥料1和2，3之间

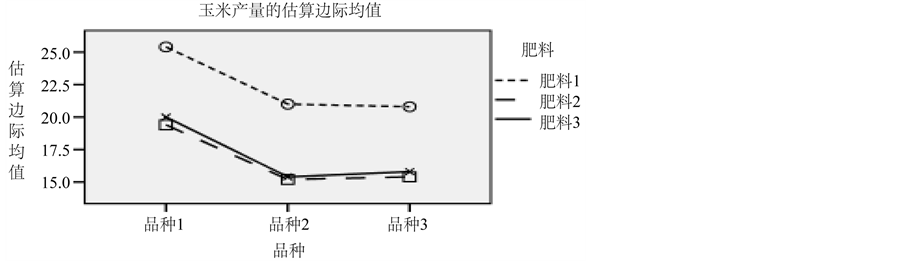
Figure 1. Interactive graphics analysis

图1. 交互作用图形分析

Table 4. LSD multiple comparisons (variety)

表4. LSD多重比较(品种)

基于观测到的均值。误差项为均值方(错误) = 2.589。^*均值差值在 0.05 级别上较显著

Table 5. Variety deviation comparison

表5. 品种偏差对比

Figure 2. Box-plot (variety)

图2. 箱线图(品种)

Table 6. LSD multiple comparisons (fertilizer)

表6. LSD多个比较(肥料)

基于观测到的均值。误差项为均值方 (错误) = 2.589。^*均值差值在0.05级别上较显著。

Table 7. Fertilizer deviation contrast

表7. 肥料偏差对比

Figure 3. Box-plot (fertilizer)

图3. 箱线图(肥料)

对玉米产量有显著的影响，且肥料1作用下玉米的产量总体较高，均值最大，是值得我们研究的肥料品种 [9] 。

5. 方差分析假设的检验

在面向农业物联网监测数据且基于农作物生长优选环境的试验模型分析中，我们是在收集到的数据服从正态性和方差齐性以及各样本相互独立的前提假设下进行的，多以我们有必要对所做的假设进行验证。由于我们采取简单随机抽样得到样本，故保证了数据的随机性和独立性，即从各个总体中抽取的随机样本是相互独立的[10] 。结果见表8~表10。

从以上分析结果可以看到，在所有组中因变量的误差方差满足齐性，且在给定的显著性水平下，检验的p值均大于给定的水平，故满足数据分析的正态性。

6. 结论

方差分析是一种定量处理数据的统计推断分析方法。利用统计的思想和模型，定量处理面向农业物流网监测到的数据，可以从某种程度上解决农作物生长优选环境中一系列被模糊处理的问题，具有一定的应用价值。如何找到适合农作物生长的最优组合环境是农业生产中经常遇到的问题，对此我们将统计

Table 8. Levene test of equivalence property of error variancea

表8. 误差方差等同性的Levene检验^a

检验零假设，即在所有组中因变量的误差方差均相等。^a设计: 截距 + 品种 + 肥料 + 品种 * 肥料

Table 9. Normal test

表9 正态性检验

^*这是真实显著水平的下限。^aLilliefors显著水平修正

Table 10. Normal test

表10. 正态性检验

^*这是真实显著水平的下限。^aLilliefors显著水平修正

的方法与农业生产中一些问题的研究相结合，可以更加准确方便的解决需多实际问题 [11] 。

基金项目

北京市委组织部优秀人才培养资助项目(2013D005017000016)；北京市教育委员会科技计划面上项目(KM201410016003)；北京建筑大学学术创新团队(21221214111)；研究生培养–研究生教育–产学研联合培养研究生基地(2014) (31062014001)。