1. 引言
作为一种自然制冷工质,二氧化碳具有很好的环保性能和流动传热特性。这可以从根本上解决制冷系统工质替代问题,有希望成为汽车空调、热泵、商业制冷、民用商业用空调系统的制冷工质[1] 。超临界CO2是处于临界温度和临界压力以上的流体,具有很强的溶解能力和良好的流动、输运性质。
突扩管是研究流动分离和再附着现象的经典模型之一。在突扩管流中,当流动雷诺数高于临界雷诺数时,发生流动分叉现象,由对称稳态向不对称稳态转化。这已经得到了其他研究者的证实[2] -[5] 。此前关于突扩管流的研究[6] -[9] 很多,但多限于研究流动特性,关于换热特性方面的研究很少。Nie和Armaly [6] 对突扩管在流动对称区,即流动雷诺数在临界雷诺数以下,进行了三维的数值模拟。对于同样的数值模型,Thiruvengadam等[10] 研究了高于临界雷诺数时的情形,即流体在流动分岔后的稳态非对称流动时的流动和换热特性。上述研究对象都是常规流体,流体的流动是按照恒热物性处理的。对于超临界流体,流体物性变化所带来的流动和换热影响需要得到充分的考虑。Guo [11] 等研究了热效应对气体在突扩管中流动时回流区的影响,证明了回流区的大小会随着壁面加热强度的增加而减小,并指出了由于加热引起的流向的反向压力梯度导致了回流区的缩小。邓[12] 的论文研究了超临界CO2在平面突扩管中进行对流换热的数值模拟,关注了流体的流动分叉现象、雷诺数低于临界值时的对称稳态区域中加热热流密度对超临界CO2换热的影响。
本文是在邓[12] 的论文的基础上,进行深一步的探究工作,研究在冷却条件下,超临界CO2在突扩管中的流动换热情况。
2. 数值计算模型
2.1. 物理模型
数值模拟的物理模型和坐标系统如图1所示,台阶高度S = 1 mm。前方入口段和后方的突扩段的管径分别为d和D,定义突扩比为ER=D/d。参照文献[13] [14] ,入口段长度取L1 = 20 d,这足以保证来流充分发展。选取突扩段长度L2 = 60 S。上下壁面均匀冷却,热流密度分别为−100、−250、−500 W/m2均匀热流边界条件,采用零厚度无滑移壁面。
入口温度均匀分布,入口初始温度T0为313.2 K。
2.2. 数学模型
本文采用二维、层流、稳态模型计算连续方程、动量方程及能量方程。数学控制方程如下:
连续性方程
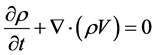 (1)
(1)
动量方程
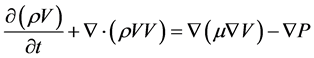 (2)
(2)
能量方程
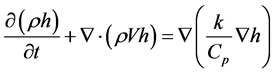 (3)
(3)
在方程(3)中,h是焓值,其定义如下:
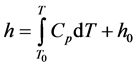 (4)
(4)
其中,h0 = 344.42 kJ/kg,是参照温度T0时的焓值。
2.3. 边界条件
实际流体流动过程中,在突扩截面处入口速度为抛物型。考虑为不可压缩问题[15] ,所以入口处采用速度入口;压力出口。边壁为固定无滑移条件。
本文采用的数值方法是有限体积法。计算工况以及网格生成参照邓[12] 的文献。采用SIMPLEC算法求解,动量和能量方程采用二阶迎风格式离散化。采用非均匀网格划分。网格独立性验证方面借鉴文献[15] 的经验,此处不再验证;网格数量也参照该文献,取300(x) × 60(y)的网格。流体的热物性是采用REFPROP数据库[16] ,采用分段函数拟合,吻合度高达99%。
3. 计算结果与讨论
3.1. 流动雷诺数的影响
参考文献[15] 可知,浮升力效应在本文的研究中可以忽略不计。选择Re分别为150、220、280、340、450进行模拟计算。图2为冷却条件下发生流动分叉后的流线图。可以看出,当Re > 150时,在突扩处流动发生分离。这是因为在突扩处压力突然减小,所以会形成上下两个回流区。

Figure 2. Streamline chart q = −100 W/m2, ER = 2
图2. 流线图q = −100 W/m2,ER = 2
入口雷诺数从一个较小值慢慢增大到一个较大值过程中,存在一个临界雷诺数(Recr),当流动雷诺数大于临界雷诺数时,回流区由开始的上下对称,发展到上下不对称,即发生流动分离现象。雷诺数继续增大,则大的回流区继续变大,小的回流区继续变小。而当雷诺数高于某一个值时,就会出现第三个回流区。这时的雷诺数称为转换雷诺数(Retr)。从图2中可以发现,在冷却条件下也符合上述规律。与图3显示的流动规律相比,冷却条件下流动规律与加热时的规律基本是一致的。
由图2可知,冷却条件下,Recr位于150附近,Retr则位于280~340之间。通过更多细致的模拟计算,对Re在150附近取更多的数进行计算,确定了上述两个雷诺数的准确值,见表1;加热和不施加条件[15] 情况下的Recr和Retr也列于下表。
对表1中数据分析可知,在相同的热流密度下,冷却和加热时的临界雷诺数和转换雷诺数差异较大。在相同的条件下,冷却时流动更易发生分叉。
3.2. 热流密度的影响
突扩管模型中,回流区的大小是很重要的参数,因为其决定了整个流场的特性,相应的对流换热也与之交互影响。分离流体的再附着点距原点的距离定义为回流区的长度XR。图4给出了在冷却条件下无量纲的回流区长度(XR = Xr/S)在不同壁面热流条件下随雷诺数的变化。图5 [15] 则是加热情况的无量纲回流区长度随雷诺数的变化
对图4分析可知,冷却条件下,Re一定时随着冷却热流密度的增大,回流区长度减小。而图5显示的规律则与之相反,随着加热热流密度的增大,回流区长度也增大。

Table 1. Recr and Retr of supercritical CO2 in sudden expansion duct under different heat transfer conditions (ER = 2)
表1. 不同换热条件下超临界CO2在突扩管中的Recr和Retr (ER = 2)
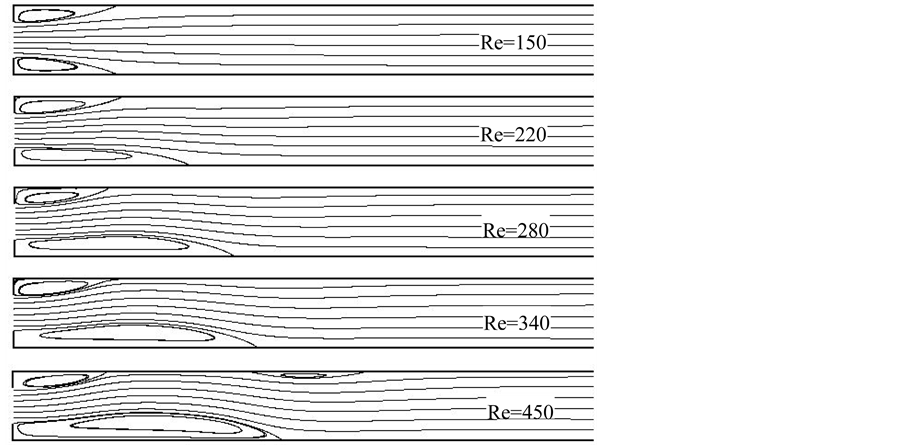
Figure 3. Streamline chart q = 100 W/m2, ER = 2 [15]
图3. 流线图q = 100 W/m2,ER = 2 [15]
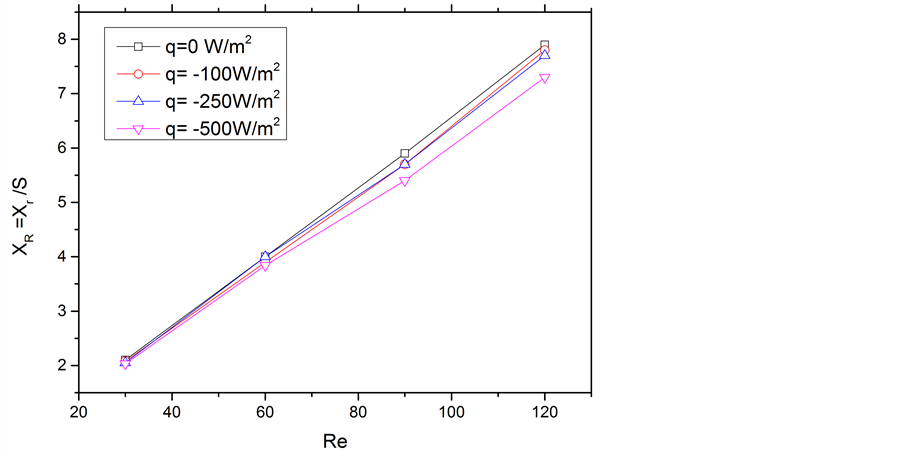
Figure 4. Variation of reattachment length with Reynolds at different wall flux under cooling condition
图4. 冷却条件下,不同壁面热流下回旋区长度随雷诺数的变化
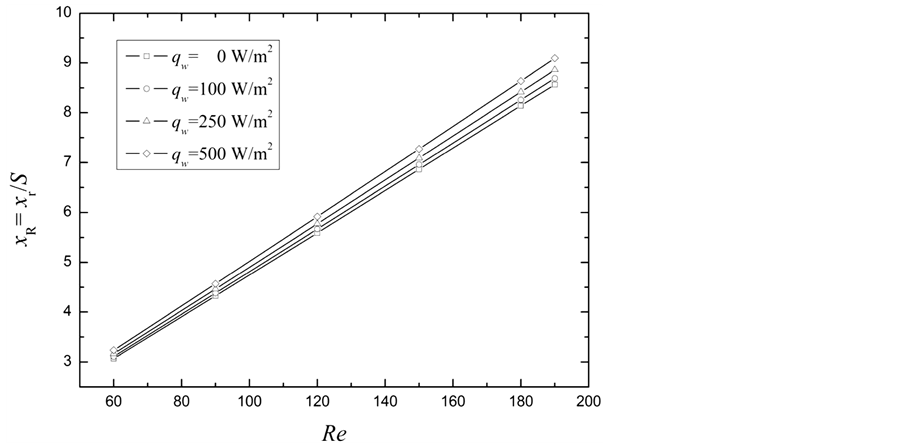
Figure 5. Variation of reattachment length with Reynolds at different wall flux under heating condition [15]
图5. 加热条件下,不同壁面热流下回旋区大小随雷诺数的变化[15]
4. 结论
本文研究了超临界CO2在平面对称突扩管中,在冷却条件下的流动换热。这是在前人研究的基础上的深入和验证,得到以下结论:
1) 冷却条件下,与超临界CO2加热条件下的规律基本一致,随着流动雷诺数的增大,流动由对称发展为不对称,进而出现第三个或者更多的回流区。这是对常规流体流动规律和超临界CO2加热条件下流动规律的补充。
2) 在冷却条件下超临界CO2的流动情况,和在加热条件下对应的情况比较,临界雷诺数和转换雷诺数都明显减小。这意味着在冷却条件下超临界CO2流动更易失稳,易发生流动分叉。
3) 在冷却条件下,随着冷却热流密度的增大,回流区长度减小。
致谢
感谢国家自然科学基金项目(项目号:51476001)的支持。
*通讯作者。